
行测图形推理:必会考点之对称性
图形推理这一模块考点多、难度大,但出题规律也极强,通过总结梳理真题中的考点很容易达到事半功倍的效果。今天就为大家介绍一个图形推理中的常考点:对称性。
对称性的常规考法是看对称形式(所给图形属于轴对称或中心对称或既轴对称又中心对称或者完全不具备对称性)、看对称轴条数、看对称轴方向,这些常规考法通常难度较低。但随着考试难度的加大,对称性这一考点也出现了难度升级的情况,新花样包括什么呢?
一、对称图形的分类
在图形推理的题目中,常见的对称图形主要分为三种类型:轴对称图形、中心对称图形和轴+中心对称图形。
轴对称图形:如果一个图形沿着一条直线对折后两部分完全重合,那么这个图形叫做轴对称图形。如字母图形“B”,或等腰三角形等。轴对称图形的对称轴条数可以为1条或者多条;对称轴的方向可分为横轴、纵轴、斜轴等。
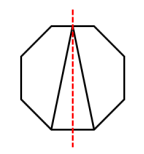
中心对称图形:如果一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形叫做中心对称图形。如字母图形“z”,或者平行四边形等。
轴+中心对称图形:如果图形既是轴对称图形、又是中心对称图形,那么这个图形叫做轴+中心对称图形。如字母图形“H”,或者正多边形(如四角星、六边形)等。值得注意的是一个图形既轴对称又中心对称一定有两条或两条以上的对称轴。
除此之外,大家还要注意旋转对称图形。旋转对称图形是指图形围绕着某个点旋转一定的角度(旋转角度大于0°,小于360°)后与原图成对称关系的图形。比如五角星就是旋转72°之后可以与原图重合。常见的旋转图形有正多边形,圆,平行四边形等。一般而言,所有的中心对称图形都是旋转对称图形,但是旋转对称图形不一定是中心对称图形。
二、对称图形常见考点
1.对称的类型
当图形形状不一,数量上没有规律或者有明显的对称图形时,可以考虑对称的规律。最常见的就属对称类型的考查了。在这里主要考查的是判别图形是非对称图形还是对称图形,是轴对称图形、中心对称图形还是轴+中心对称图形的能力。
例1:把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:( )

A.①④⑥,②③⑤ B.①③⑥,②④⑤
C.①②⑥,③④⑤ D.①②④,③⑤⑥
【答案】D【解析】第一步,观察特征。组成元素不同,优先考虑数量类或属性类,此题对称特征明显,考虑对称性属性。第二步,根据规律进行分组。观察发现,图形①②④是轴对称图形,图形③⑤⑥是中心对称图形,分为两组。因此,选择D选项。
2.对称轴的方向
当出现的图形是轴对称图形,而且图形的对称轴只有一条时,图形的对称轴在方向上往往会呈现出统一或者动态旋转变化一定角度的规律。
例2:从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:( )
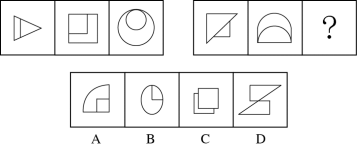
【答案】C【解析】第一步,观察特征。组成元素不同,优先考虑属性类或数量类。对称特征明显,考虑属性类对称性。第二步,两段式,第一段找规律,第二段应用规律。第一段三个图形均为轴对称图形,对称轴方向分别为:横轴、斜轴(\)、竖轴,即对称轴依次顺时针旋转45°;第二段应用规律,前两图的对称轴方向为斜轴(\)、竖轴,问号处应为斜轴(/),只有C项符合。因此,选择C选项。
3.对称轴的数量
当出现的图形是轴对称图形,而且图形的对称轴不只一条时,多考查对称轴的数量。图形的对称轴在数量上可能会呈现出常数、等差、运算或者是对称轴的数量与图形中的面、线、角、点的数量之间的关系等规律。
例3:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:( )

【答案】D【解析】第一步,观察特征。组成元素不同,优先考虑数量类或属性类,对称特征明显,考虑属性类对称性。第二步,九宫格,横向规律较为常见,优先考虑。第一行中三个图形的对称轴条数分别是1、1、2;第二行中三个图形的对称轴条数分别是1、2、3;前两个图形的对称轴条数之和等于第三个图形的对称轴条数。第三行应用规律,前两个图形的对称轴条数分别为2、3,2+3=5,所以问号处的图形应有5条对称轴,只有D项符合。因此,选择D选项。
4.对称轴与图形的关系
当出现的轴对称图形在对称轴的数量和方向上找不到规律时,可以观察对称轴与图形中的线是否存在垂直或重合等关系。
例4:把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:( )

A.①③④,②⑤⑥ B.①②⑥,③④⑤
C.①④⑤,②③⑥ D.①④⑥,②③⑤
【答案】C【解析】第一步,观察特征。图形组成元素不同,优先考虑数量类或属性类,对称特征明显,考虑属性类对称性。第二步,依据规律进行分组。图形均有对称性,其中图形①④⑤的对称轴均与原图的线条垂直,图形②③⑥的对称轴均经过原图形的交点,分为两组。因此,选择C选项。
5.图形与图形之间对称轴的关系
当图形是由若干个对称图形组成的,可以观察各个部分的对称轴之间的关系。
例5:从所给的四个选项中,选出最合适的一个填入问号处,使之呈现一定的规律性:( )
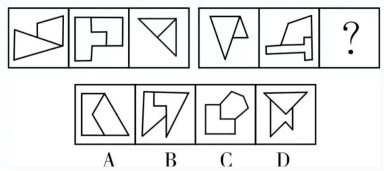
【答案】D【解析】第一步,观察特征。组成元素不同,优先考虑数量类或属性类,每幅图形均由两个对称图形组成,考虑对称性。第二步,两段式,第一段找规律,第二段应用规律。第一段,每幅图中两个图形对称轴的夹角分别为0°、45°、90°;第二段应用此规律,前两幅图形中两个图形对称轴夹角分别为0°、45°,所以问号处应为90°,如下图所示,只有D项符合。
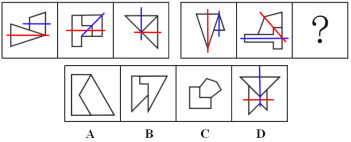
因此,选择D选项。
三、新花样难度升级考法
1.考查对称轴与原图形的关系。
如对称轴经过原图形的交点、对称轴与原图形的线条重合等。
【例】把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:( )

A.①⑤⑥,②③④ B.①②④,③⑤⑥
C.①②⑤,③④⑥ D.①③④,②⑤⑥
【答案】C【解析】第一步,观察特征。组成元素不同,优先考虑数量类或属性类。图形规整,优先考虑属性类中的对称性。第二步,根据规律进行分组。所有图形均是轴对称图形,将其对称轴画出,如图所示:
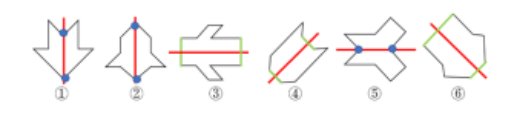
观察发现,图①②⑤对称轴贯穿图形交点,图③④⑥对称轴贯穿图形两条平行线,据此分为两组。因此,选择C选项。
【点拨】以上题目考查的是对称轴与原图形的关系,是过原图形的交点还是过原图形的线。
2.考查局部对称形式。
图形整体不存在对称规律,但每幅图形局部存在对称特征。
【例】把下面的六个图形分为两类,使每一类都有各自的共同特征或规律,分类正确的一项是:( )

A.①②④,③⑤⑥ B.①③⑤,②④⑥
C.①②⑥,③④⑤ D.①④⑥,②③⑤
【答案】D【解析】第一步,观察特征。组成元素不同,优先考虑数量类或属性类。且每个图形黑点排布对称性明显,优先考虑对称性。第二步,根据规律进行分组。图形①④⑥中黑点的排布呈轴对称关系,图形②③⑤中白点的排布呈轴对称关系,分为两组。
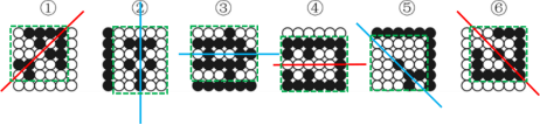
因此,选择D选项。
【点拨】其实这个题就是考一个局部的思维,要求考生能将黑白球分开看,即考查局部对称形式。
3.考查对称轴两边的图案特征。
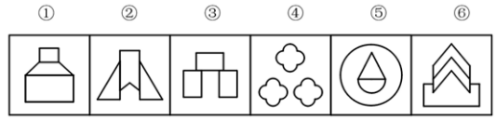
【例】把下面的六个图形分成两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:( )
A.①②③,④⑤⑥ B.①④⑤,②③⑥
C.①③⑤,②④⑥ D.①⑤⑥,②③④
【答案】D【解析】第一步,观察特征。组成元素不同,对称特征明显,优先考虑对称性。第二步,根据规律进行分组。题干六个图形都是竖轴对称,②③④中对称轴两侧均有形状相同的小元素,如②中左右两个三角形、③中左右两个矩形、④中左右两个花朵;①⑤⑥对称轴两侧不存在形状相同的小元素,分为两组。因此,选择D选项。
【点拨】以上题目考查的是对称轴两侧的图案特征,即是否存在独立的小元素。








