
行测图形推理中黑白球和黑白块考查
黑白“双煞”
黑白球,黑白点,黑白色块,在公考中是常考考点,从真题的命题趋势来看,几乎每年都有涉及,并且近期的难度也不低,接下来我们就一同来看看黑白球,黑白点,黑白色块的真题出题方向。
黑白球,黑白点,黑白色块常见的考点我们一般说到是有6个。
第一,个数问题,也就是本身的数量关系可能会出题。
第二,移动。如果个数相同,我们可以认为图形宏观构成是相同的,可以思考位置类规律,进一步缩小范围,放在移动规律中。
第三,对称性问题,而对称性我们也能结合轴对称,中心对称,既是轴对称也是中心对称,三个方面去考虑。
第四,叠加问题,叠加问题的出题方向是结合黑白颜色来出题,也就是黑加黑,白加白,黑加白,白加黑的规律。
第五,部分数。
第六,笔画数。
往下我们先通过一些真题来感受下黑白球,黑白点,黑白色块的出题方向。
例1:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性( )。

【答案】D【解析】对称性。题干图形组成相同,优先考虑位置类规律。观察发现,第一行,黑球个数为6个,第二行,黑球个数为8个,第三行,黑球个数为10个,可以先排除选项A、B。由于每一行的个数都不同,所以,不考虑移动规律。下一个常考规律是对称性问题,观察发现,第一行都具有对称性,且对称轴方向分别为水平,斜向45度,斜向45度,因此,需要找一个斜向45度方向与图3一致的图形。故本题答案为D项。
这个题是一个较为常规黑白球,黑白点,黑白色块考法,考察个数问题和对称性问题。接下来我们来看一个近期黑白球,黑白点,黑白色块的真题,它的出题方向更加的多样。
例2:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性( )。
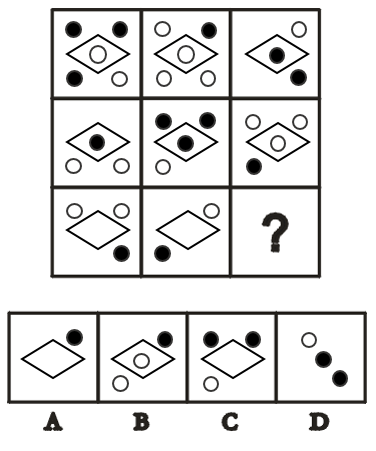
【答案】B【解析】叠加。图中都出现了黑白球,优先考虑黑白球的常考考法,第一个是个数问题,在第一行图形中,黑球个数分别为312,没有一致规律,因此也不考虑第一个移动考点。第三个考点是叠加问题,这个题型的叠加是加入了黑白和空格来考察叠加问题。黑加白=空格,黑加黑=白,白加白=黑,黑加白=空格,白加白=黑,空加黑=白,白加空=空。第二行验证的确可行,把它运用在第三行。第三行左上位置是白加空=空,先排除CD。左下角位置是空加黑=白。故本题答案为B项。
从图形的宏观特征来看,图形构成相同,考虑位置类规律。图形构成相似,考察样式规律。图形构成凌乱,考察数量关系。
总结:>>
1.何时考黑白球,黑白点,黑白色块?
答:宏观来说,图形识别有黑白球,黑白色块,黑白点的出现。
2.怎么做?
答:先用图形的宏观特征想通过,相似,凌乱缩小范围,再用黑白球,黑白点,黑白色块常见的6类考法确认最后的考点,第一,个数问题。第二,移动。第三,对称性问题。第四,叠加问题。第五,部分数。第六,笔画数。
你看得懂“黑白色块”的世界吗?
“黑白色块”在图形推理当中的考频较高,并且其考法不仅比较灵活还比较复杂。面对“黑白色块”,怎样才算是心中有数?“黑白色块”到底有哪些考法?怎样才能快速锁定考点并且选出答案?接下来,就让我们一起走进“黑白色块”的世界吧!
当看到“黑白色块”考题出现时,首先要观察其图形构成。
#如果题目中黑块与白块数量完全相同:
大概率会考查位置类规律,因此块数相同优先考虑位置类规律。
#如果题目中黑块与白块数量有略微不同(如图所示):
大概率会考察黑白叠加运算,要注意黑白叠加运算一般不会以分组分类的形式命题,因此块数不同且不是分组分类,优先考虑黑白叠加运算。

那当“黑白色块”杂乱无章的情况出现,我们又当如何应对?
这一类题目大概率会考察对称、笔画、部分数、面积等其他规律。先从“黑白色块”对称性的考点来说,可能考察对称形式(轴对称、中心对称)、对称轴(方向、数量)等,简单来说就是把对称性的很多考点融合到“黑白色块”的题型中。
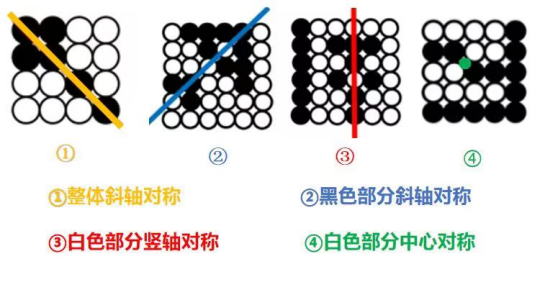
#如果黑块连接成一条线,并且有明显的直角拐弯:
我们优先考虑笔画问题,可以理解为黑色部分最少需要几笔连起来,当然也可以关注白色部分的笔画数。
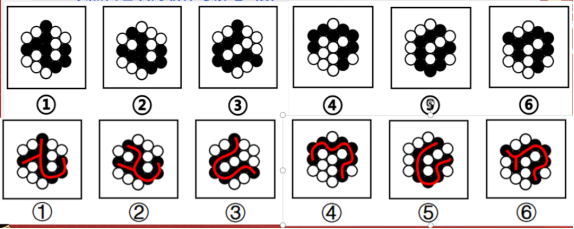
#如果黑色块有明显的分堆,或明显多个部分:
我们优先考虑部分数,同样的需要注意黑白分开数,可能考察黑色部分数和白色部分数之间的运算。








