整除法解决计算问题

数量关系是在行测中对大多数考生来说都比较难的部分，但是如果我们能够掌握一类题型的做题思路，相对来说就会对没有那么强的畏难情绪。接下来就带领大家一起来学习整除法。

一、整除与除尽的概念

1、整除：若整数“a”除以大于0的整数“b”，商为整数，且余数为零，我们就说a能被b整除。

2、除尽：两数相除，没有余数，这时就说被除数能被除数除尽。整除是除尽的一种情况。

二、常用小数字的整除判定

1、局部看

(1)一个数的末位能被2或5整除，这个数就能被2或5整除;

(2)一个数的末两位能被4或25整除，这个数就能被4或25整除;

(3)一个数的末三位能被8或 125 整除，这个数就能被8或125整除;

2、整体看

(1)整体作和：一个数各位数数字和能被3或9整除，这个数就能被3或9整除。

(2)整体作差：如果一个整数的末三位与末三位以前的数字组成的数之差能被7、11或13整除，那么这个数能被7、11或13整除。

三、整除的应用环境

1、文字描述整除：明显整除字眼、出现“每”“平均”“倍数”;

2、数据体现整除：出现分数、百分数、比例等。

四、整除的应用

例1.若干学生住若干房间，如果每间住4人，则有20人没地方住;如果每间住8人，则有一间只有4人住，问共有多少学生?

A.30          B.34            C.40          D.44

【答案】D。解析：题干中出现“每”，可以考虑用整除。每间住4人，则有20人没地方住，说明(总人数-20)能被4整除，20能被4整除，也意味着总人数能被4整除，排除A、B选项。每间住8人，则有一间只有4人住，说明(总人数-4)能被8整除，排除C选项，故选择D选项。

例2.公司四名促销员某月共推销新产品100件，甲与丁共推销64件，甲与乙销量的比例为5:3，丙与丁销量的比例为1:2，则甲该月推销了多少件?

A.20          B.28          C.38          D.40

【答案】D。解析：题干中出现比例，可以考虑用整除。求甲的销量，而甲与乙销量的比例为5:3，则甲的销量能够被5整除，排除B、C选项。代入A选项，若甲为20，则根据甲、乙比例关系，乙为12，丁为44，丙为22，加和为98，不满足和为100，排除A选项，故选择D选项。

通过上述例题，相信大家对于整除法解决计算问题已经有了进一步的认识。希望大家接下来可以多多练习，进一步将理论内化于心。

等差数列原来如此重要

在近年来的公职类考试数量关系中，计算问题备受出题老师青睐，在考试中的占比也在不断提升，而在计算问题众多的考查题型中，等差数列作为相对而言比较重要的一个知识点应该引起我们足够的重视，接下来就带大家一起来看一下等差数列。

 定义和概念 

等差数列：一个数列从第二项起，每一项与它的前一项的差等于同一个常数。

比如，数列1，3，5，7，9，11，在这个数列当中，后一项与前一项的差均为2，所以这是一个公差为2的等差数列。

首项：数列当中的第一项，用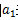表示。

末项：数列当中的最后一项，用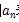表示。

公差：固定的差值，用d表示。

前n项和：用表示。

 基本公式 

1. 通项公式：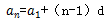

2. 2.求和公式：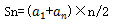

中项求和公式：

 典型例题 

某学校组织活动进行队列训练，学生们组成一个25排的队列，后一排均比前一排多4个学生，最后一排有125个学生。则这个队列一共有( )个学生。

A.1925          B.1875          C.2010          D.1765

【答案】A。解析：根据题目信息后一排均比前一排多4个学生，可以判断这个队列为公差为4的等差数列，其中n=25，d=4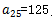，，问题所求为这个数列的前25项和。

方法一：根据通项公式，求出第一项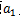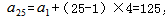，，解得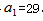。根据等差数列前n项和公式，可得，共有1925个学生。选A。

方法二：直接求中间项，则等差数列和为。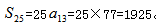

通过例题的讲解，相信大家已经对等差数列的相关知识点有了一定的了解，等差数列作为计算问题中比较重要的一个知识点需要各位同学重点掌握，相信各位同学经过不断的练习和总结一定能够很好的解决这部分题型。

数量关系之日期问题

行测的数量关系经常会涉及到日期问题。对于日期问题，我们需要掌握基本的常识和计算方法，在此基础上多做题，在考场上遇到相关题目时，才能够灵活应对。

 基本常识问题 

1、平年、闰年判定方法

(1)闰年：非整百年份，能被4整除，则这年为闰年;整百年份，能被400整除，则这年是闰年。

(2)平年：非整百年份，不能被4整除，则这年为平年;整百年份，不能被400整除，则这年是平年。

2、大月份、小月份、特殊月

(1)大月份：有31天的月份，分别为：1月、3月、5月、7月、8月、10月、12月。

(2)小月份：有30天的月份，分别为：4月、6月、9月、11月。

(3)特殊月：2月份，闰年的2月有29天，平年的2月有28天。

3、星期：周期为7天

(1)平年每过一年，星期往后推一天。(共365天，365÷7=52…1，故往后推一天)

(2)闰年每过一年，星期往后推两天。(共366天，366÷7=52…2，故往后推两天)

 例题精炼 

例1.2012年6月1日是星期五，那么2011年6月1日是( )?

A.星期三         B.星期四         C.星期五         D.星期六

【答案】A。解析：2011年6月1日到2012年6月1日，是过了一整年，过的2月份是在2012年，而2012年能被4整除，所以2012年为闰年，所以过了366天，366÷7=52…2，故星期往后推了两天，2012年6月1日是星期五，所以2011年6月1日往前推2天为星期三。此题，最终答案选择：A。

例2.某年9月份共有5个周六、5个周日，请问这一年9月15日是周几?

A.周四           B.周五           C.周六          D.周日

【答案】C。解析：9月份有30天，其中包含4个整星期，故必定包含4个周六、4个周日。通过9月份有5个周六、5个周日，说明月份最后的两天29日、30日分别为周六、周日。9月15日到29日，是过了14天，即两个整星期，所以15日和29日星期数相同，9月15日为星期六。此题，最终答案选择：C。

例3.1896、1948、1988、2000、2012、2020，下列年份中与上述年份具有相同的规律的年份是( )年?

A.1600           B.1900           C.2010           D.2018

【答案】A。解析：以上已知年份都为闰年，在选项中选择一个闰年即可。 A、B选项为整百年，判定时候是除400，发现A为闰年，B为平年;C、D选项为非整百年，判定时候除4，发现C、D都为平年。选项中只有A为闰年。此题，最终答案选择：A。

各位同学，对于日期问题，大家一定要记住基本的常识和计算方法，并且多加练习相关题目，从而不断巩固我们的相关知识。

两个公式解决等差数列问题

等差数列是行测数量关系中比较基础的知识，是数学思维中一类发现规律、总结规律、应用规律题型的具体体现。也是我们公职类考试中，可能考查的知识点之一。对于等差数列的问题，我们主要根据两个公式解决问题，分别是通项公式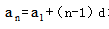：和求和公式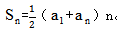：。下面带大家一起用这两个公式来解决一下下面的问题：

例1.某个月有五个星期六，已知这五个日期的和为85，则这个月中最后一个星期六是多少号?

A.10           B.17           C.24           D.31

【答案】D。解析：每两个相邻星期六之间都是过了7天，也就是公差为7的等差数列，根据某个月五个星期六的和为85，得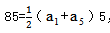，且根据通项公式知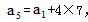，解得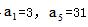。选择D选项。

通过刚才的题目，可以发现，对于一个数列而言，当相邻两项的差值一定时，就可以通过等差数列的两个公式来求解。对于求解数列中任意一项的问题，往往用通项公式来解决;求解数列中几项和的问题，往往用求和公式来解决。我们再看一道稍微有些难度的问题：

例2.生产同一批产品有两种方案。方案一：第一天生产1件，往后每一天比前一天多生产2件，12天正好完成任务;方案二：第一天生产量未知，往后每一天比前一天多生产1件，9天正好完成任务。问两种方案的第7天生产量相差几件?

A.7         B.6          C.5          D.4

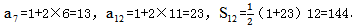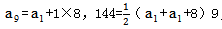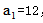【答案】C。解析：根据后一天分别比前一天多生产2件和1件，可以判断两种方案分别是公差为2和1的等差数列。根据“方案一：第一天生产1件，往后每一天比前一天多生产2件，12天正好完成任务”，可得。再由“方案二：第一天生产量未知，往后每一天比前一天多生产1件，9天正好完成任务”，可得，解得，此时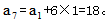。两种情况下第7天相差18-13=5件。选择C选项。

通过上述两道题目，小伙伴们掌握到等差数列公式的应用了吗?建议各位考生在后面的学习中，一定要多多练习和应用，熟练判断等差数列的题目，并将两个公式运用纯熟，才能在考场上如鱼得水。