资料分析中的混合问题
在公务员考试行测中资料分析是行测的重要组成部分，对于大家来说资料分析要达到90%以上的正确率，就得攻克一些比较难的题目，比如混合问题。对于混合问题，我们不仅得知道混合问题的结论，还得知道混合问题在什么样的题目运用。所以在这里为大家带来溶液的混合问题。
混合问题的本质其实就是溶液的浓度混合问题。所以我们得知道溶液混合的三个结论：
1.两杯不同浓度的溶液混合，混合后的浓度介于混合前两杯溶液的浓度之间。
比如：将浓度为5%的盐水和清水(可以理解为0%的盐水)混合，这个过程相当于是用清水把5%的盐水稀释的过程，所以混合后的浓度必然要比5%小，同样不可能把盐水浓度稀释为0。所以说混合后的浓度就在0%-5%之间。
2.如果两杯溶液的质量之比是1：1，那么混合后的浓度就是混合前两个浓度的中间值。
比如:将mg浓度为5%的盐水和mg浓度为10%的盐水混合，两者混合后的浓度就应该是
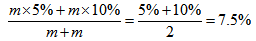
3.将两杯不同浓度的溶液混合，两杯中哪杯的溶液的质量大，混合后的浓度就介于两者的中间值和溶液质量大的这杯的浓度之间。
比如：将mg浓度为5%的盐水和ng浓度为10%的盐水混合(m＞n)，两者混合后的为：
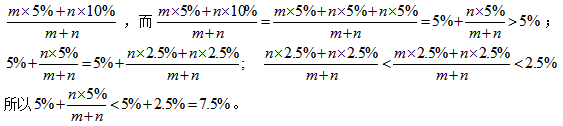
在浓度混合问题中，我们知道浓度的计算公式是：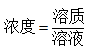
，所以混合问题的所涉及的概念本质要是
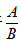的列式。其次在概念上来说，一个整体由若干部分组成，整体的分子是若干部分的分子加和，整体的分母是若干分母的加和。在资料分析中常见的混合问题有混合增长率，混合比重，混合平均数。
例.已知2019年1-2月中国粮食的出口量为48万吨，同比增长了1.7%，3月的粮食出口量为30万吨，同比增长了34.6%，则2019年1-3月中国粮食的出口量同比增长了百分之几?
A.34.6% B.20.5% C.12.2% D.1.7%
【答案】C。解析：这道题已知1-2月和3月粮食的同比增长率，求1-3月的增长率，从时间概念来说，1-3月就是由1-2月和3月组成，所以相当于已知两个部分对应的增长率，而求整体的增长率。我们知道增长率的定义式是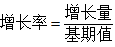
，属于
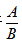的列式。而且1-3月的增长量=1-2月的增长量+3月的增长量，1-3月的基期值=1-2月的基期值+3月的基期值。所以这道题我们可以运用混合问题的三个结论去做，考查混合增长率。我们可以这样理解，这道题相当于将浓度为1.7%的溶液和浓度为34.6%的溶液混合，利用结论1，我们知道混合后的浓度应该大于1.7%，小于34.6%。所以选项A，D错误，排除。利用结论3，我们需要知道哪个浓度所对应的溶液的量大，对于这道题，溶液的量相当于就是分母上的基期值，我们得判断谁的基期值大，我们知道两个现期值如果相差较大的话，现期值大的基期值对应也大，所以我们可以通过现期值的大小去判断基期值的大小。很显然，1-2月的基期值要大一些，所以混合后的增长率就应该更加靠近1-2月的增长率1.7%，也就是介于1.7%和两者的中间值之间，而1.7%和34.6%的中间值为
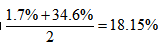。所以1-3月的增长率应该介于1.7%-18.15%之间，选C选项。
在行测资料分析中，混合问题也是常常会考到的一个难点，希望同学们能够结合我们所讲的混合问题的三个结论和其应用环境，能够将混合增长率问题，混合比重问题，混合平均数问题搞清楚，再通过相关题目的练习掌握这个考点。
正反比速解行测问题
在行测考场上，每位考生都是跟时间赛跑的人，基本上谁赢得了时间就赢得了胜利。所以能找到快速解题的方法，真可谓是所有考生一直梦寐以求、不断追求的目标。那么下面就给大家介绍一下利用正反比如何快速解题。
例1.上午8点，甲、乙两人从A、B两地同时出发相向而行;9点，二人相距54千米，二人继续前进，到上午11点，二人第二次相距54千米。已知甲每小时比乙多走3千米，那么A、B两地距离为( )千米?
A.100 B.108 C.114 D.136
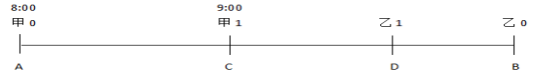
【答案】B。解析：题干描述了甲乙两个人在不同时刻的行进过程，那么可以通过行程图来梳理两人在不同时刻的位置(11点时刻未画出)。本题可以通过等量关系得出两人在9点至11点走的路程和54+54=(V甲+V乙)×2，且V甲=V乙+3，可得V甲=28.5千米/小时，V乙=25.5千米/小时。因此，AC=28.5×1=28.5，DB=25.5×1=25.5，所以AB=28.5+54+25.5=108。
题目虽然解出来了，但是相对比较复杂，这一题如果利用在整个行进过程中，两人速度不变，那么8点到9点行进1小时，9点到11点行进2小时，那么时间比等于路程比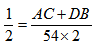
，因此，得到AC+DB=54，AC+DB+CD=AB=54+54=108。所以正确答案为 B。
例2.A、B两列车同时从甲地到乙地，A车到达乙地立即返回，返回途中与B车相遇，相遇点距乙30千米，相遇后A车经过4小时返回甲地，B车0.5小时到乙地，则A车往返一趟需多少小时?
【答案】B。解析：如图所示，题干描述了A、B两列车在甲乙两地之间的行进过程，可以通过行程图来梳理两人不同时刻的位置。A、B两人同时从甲出发，当A车折返后在丙地与B相遇。若设B从甲地到丙地的运动时间为x，由于甲地到丙地之间路程一定，则有时间与速度成反比，可得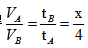
。乙地到丙地之间路程一定，则有
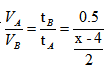。因此，
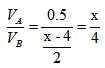，解得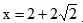
，故而所求为
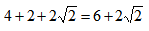，因此选择B选项。
通过上面两道题的示例，大家应该发现了利用正反比解题，一方面能节约做题时间，另一方面还能帮助大家找寻等量关系，是快速解题的不二法门。所以希望各位积极备考的考生能在考试中能得以应用，提高自己做题的速度和准确率。相信通过大家的努力，一定能够掌握好这类问题，把握住考试机会。
提炼经济概念，解决复杂利润问题
近年来考试不断推陈出新，对比之前的常规题目而言，所测查考点在原有的基础上更加综合。今天给大家带来的是如何通过提炼经济概念，借助方程以及基本公式解决复杂利润问题的基本方法，其解题核心在于充分梳理题干条件，建立题干之间的等量关系，进而求解的过程。方程思想是行测中解决实际问题的一把利剑，利用方程把文字描述转换成数学语言，进而解决实际问题。
基本公式
经典例题
例1：某产品成本是200元，售价是292元，公司根据市场情况调整了销售方案，将售价调整为268元，预计日销量将上涨15%。现欲通过改进生产线降低成本，以保持降价前的单日利润，则单件产品的生产成本至少需要降低多少?
A.4% B.5% C.6% D.8%
【答案】C。解析：根据题目描述提炼经济概念分别为成本、售价、日销量以及单日利润，分别写入表格中。设原来的日销量为x，后来的成本为y，补充表格。
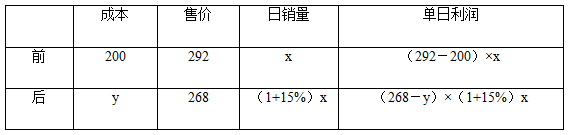
根据前后单日利润相同列等式，所以有：(292-200)×x=(268-y)×(1+15%)x
解得y=188。故所求为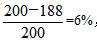
，答案为C。
例2：某家具店购进100套桌椅，每套进价200元，按期望获利50%定价出售。卖掉60套桌椅后，店主为了提前回收资金，打折出售余下的桌椅。售完全部桌椅后，实际利润比期望利润低了18%。问余下的桌椅是打几折出售的?
A.75折 B.82折 C.85折 D.95折
【答案】C。解析：根据题目描述提炼经济概念分别为销量、进价、售价以及单日利润，分别写入表格中。设原来的销量为x，成本设为y，由题意可知降价后的手机
单价为2598-300=2298元。具体关系如下：
根据题干所给“售完全部桌椅后，实际利润比期望利润低了18%”，可得：6000+(y-200)×40=(300-200)×100×(1-18%)，解得y=255。根据打折率的基本公式：
，所以余下的桌椅打85折出售。答案为C。
伴随行测的不断发展，利润问题向着更综合的考查方向延伸，对于复杂的利润问题考生要学会梳理题干信息，提炼经济概念，列出等量关系，与方程的基本思想充分结合，会给解题带来更多的便捷。
