2021国家公务员考试行测备考
数量不容易，整除来帮你
在公务员行测考试中，数量关系往往比较难，耗费时间多，众多考生这部分内容学得一般，导致考试分数不理想。带领大家学习一种比较简单的技巧去求解一系列问题，这就是“整除法”。
利用整除法去解题，不需要分析题干中的所有条件，不需要层层递进的分析题干中各种数量之间的关系，重点在于抓住题干中的一句话，或者一个简单的符号来分析问题，排除错误选项，这也是整除法的核心。
整除法的应用环境
文字描述整除：题目中出现“平均”“倍数”“每”“整除”字眼
例1.哥哥和弟弟各有若干本书，如果哥哥给弟弟4本，两人的书一样多;如果弟弟给哥哥2本，哥哥的书是弟弟的4倍，哥哥和弟弟共有( )本书。
A.20 B.9 C.17 D.28
【答案】A。解析：当哥哥给弟弟四本书之后，两人的书一样多，说明两人书的总数为偶数，排除B、C;当弟弟给哥哥2本后，哥哥的书是弟弟的4倍，则两人书的总数是5的倍数，只有A满足。
例2.一些员工在某工厂车间工作，如果有4名女员工离开车间，在剩余的员工中，女员工人数占九分之五;如果有4名男员工离开车间，在剩余的员工中，男员工人数占三分之一。原来在车间工作的员工共有( )名。
A.36 B.40 C.48 D.72
【答案】B。解析：根据题意，员工总数减去4后能被9整除，只有选项B满足。
巩固提升
1.两箱同样多的蛋黄派分别分发给两队志愿者做早餐，分给甲队每人6块缺8块，分给乙队每人7块剩6块，已知甲队比乙队多6人，则1箱蛋黄派有( )块。
A.120 B.160 C.180 D.240
【答案】B。解析：由题意“甲队每人6块缺8块”可知，1箱蛋黄派的数量加上8能被6整除，只有B项满足。
2.一菜店有大白菜和萝卜共147筐，取出大白菜的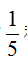
和3筐萝卜送给某学校，剩下的大白菜和萝卜的筐数相等。菜店原有大白菜和萝卜各( )筐。
A.85，80 B.80，67 C.75，72 D.70，57
【答案】B。解析：大白菜取出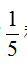
后剩下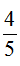
，则剩下的大白菜筐数是4的倍数。剩下的大白菜和萝卜筐数相等，因此萝卜的筐数减3后应该为4的倍数，据此排除A、C、D，选B。
“另类”增长——拉动……增长
程中关键是公式的记忆，而现在省考对于一些了解性的概念考查越来越多了。其中，拉动……增长是这些概念中相对比较常考的公式。接下来就由带领大家一起来学习拉动……增长，让大家来进一步了解拉动……增长的相关知识点。
一、含义：
用于分析某部分的增长量拉动整体增长程度的指标，一般指整体中某部分的增长量与整体基期值的比值，表述为拉动……增长……百分点。
二、计算公式
四、拉动……增长的应用
例1.2012年4月份浙江省规模以上工业增加值884.9亿元，同比增长5.6%。1-4月，规模以上工业增加值3191亿元，增长5.1%。
问题：2012年4月份浙江省规模以上工业增加值拉动1-4月规模以上工业增加值增长了多少个百分点?
解析：问题出现了拉动……增长……百分点，可以直接代入公式，拉动前面的4月浙江省规模以上工业增加值为部分，拉动后的1-4月浙江省规模以上工业增加值为整体，
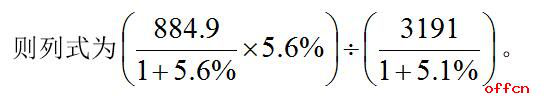
例2.2016年1-7月份，我国第三产业投资179362亿元，增长10.8%，增速比第二产业高7.3个百分点，占GDP的比重为57.5%，比第二产业高18个百分点。特别是高技术服务业、科教文卫等领域投资均保持良好的增长态势，高技术服务业投资额为7200亿元，增长18.6%。
问题：2016年1-7月份，我国高技术服务业投资额拉动第三产业投资增长多少个百分点?
解析：问题出现了拉动……增长……百分点，可以直接代入公式，拉动前面的高技术服务业投资额为部分，拉动后的第三产业投资为整体，则列式为
通过上述四道例题，相信大家对于拉动……增长这个知识点已经有了一定的认识，接下来还是需要多多做题，不断实践。希望通过以上例子能给大家一些启发!
利用整除特性解决计算问题
行测考试中的数量关系部分一直是令同学们比较头疼的问题，考试时候比较浪费时间，并且准确性也不高，所以同学们一直想获得读完题目就可以选出选项的能力。其实有一些计算问题我们确实是可以利用较短时间求解出来的，那么什么时候可以应用呢?接下来就为大家介绍一种利用整除特性解决计算问题的方法。
一、整除的定义
若整数b除以非零整数a，商为整数，且余数为零，我们就说b能被a整除(或说a能整除b)。
二、整除的应用环境
1.文字中描述整除：明显出现整除相关的字眼，比如“整除”“每”“平均”“倍数”“余数”“除尽”等。
2.数字中体现整除：出现分数、百分数、小数、比例等。
三、常见小数字整除判定
1、局部分析法
(1)一个数的末一位能被2或5整除，那么这个数就能被2或5整除。
(2)一个数的末两位能被4或25整除，那么这个数就能被4或25整除。
(3)一个数的末三位能被8或125整除，那么这个数就能被8或125整除。
2、整体分析法
(1)整体做和。一个数的各数位数字加和能被3或9整除，那么这个数就能被3或9整除。
(2)整体做差。把个位数字截去，再从余下的数中，减去个位数的2倍，差是7的倍数，则原数能被7整除。奇数位上数字和与偶数位上数字和之差能被11整除，则原数能被11整除。把个位数字截去，再从余下的数中，减去个位数的9倍，差是13的倍数，则原数能被13整除。
四、整除思想的应用
例1.教室里有若干个学生，走了10名女生后，男生是女生人数的2倍，又走了9名男生后，女生是男生人数的5倍。问：最初有多少名女生?
A.12 B.15 C.18 D.21
【答案】B。解析：这道题最终让我们求女生最初有多少人，我们发现女生从最初的人数走了10名之后，出现了与男生人数的倍数关系，那我们可以联想到出现倍数关系可以考虑整除特性，女生人数男生人数的5倍，说明此时女生的人数可以被5整除;那么这个被5整除的女生人数是由于最初人数走了10名之后得到的，而选项正好给的我们就是女生最初的人数，因此我们可以用选项减去10得到的数字要被5整除，观察选项，只有B选择符合。
例3.两个派出所某月共受理案件160起，其中甲派出所受理的案件中有17%是刑事案件，乙派出所受理的案件中有20%是刑事案件，问乙派出所在这个月中共受理多少起非刑事案件?
A.48 B.60 C.72 D.96
通过以上例题，相信大家对于利用整除特性求解计算问题有了一定的了解，但是为了在考场中可以节省时间，还是希望大家平时要多加练习!
