政华教育

【解析】读完题，其实很少有同学能反应过来是和定最值问题，我们来看一下它的问题，“至少有多少人能通过考试?”，总人数是100人，即通过与不通过总共100人，所以它还是两个数加和固定，求某个量的最小值的问题。那现在我们不妨把要求的能通过考试的人数设为x，没通过的人数设为y，那么就有x+y=100 ，如果此时我们能再列出一个关于x、y的方程并且把它们解出来就完美了，我们再看一看其他的条件，答对3、4、5道题目的人能通过考试，反过来答对0、1、2道题目的人不通过，而答对的题目总数为80+92+86+78+74=410道，所以可以列式为(3，4，5)x+(0，1，2)y=410 ‚，此时要怎么做才能得到x的最小值呢?这里老师就要给大家介绍“六字口诀”了，叫做：“小系数，同方向”。具体什么意思以及如何操作呢?

第一点，“小系数”，小系数指的是x，y两组未知数前的系数相对小的，很显然这里应该是y的系数(0，1，2)这组。那么到底取0还是1还是2呢?我们看第二个点，“同方向”，问题中求的是x的最小值，因此y的值就要最大，因此y的系数也取相对大的2。再看x的系数，在(3，4，5)中怎么确定呢?这里告诉大家，要跟y同方向确定，即取相对最大的5。则有5x+2y=410，联立x+y=100，可解得x=70，所以至少有70人能通过考试。

【总结】“小系数，同方向”中“小系数”指的是从两组系数中相对小的一组入手;“同方向”有两层内容，第一层指的是若所求为最大值，小系数的几个值中取最大的，若所求为最小值，小系数的几个值中取最小的;第二层指的是另一个组系数大小的确定与小系数这组所取方向一致。

清楚了“小系数，同方向”如何解题后，来道例题巩固一下。

【巩固训练】书法大赛的观众对5幅作品进行不记名投票。每张选票都可以选择5幅作品中的任意一幅或多幅，但只有在选择不超过2幅作品时才为有效票。5幅作品的得票数(不考虑是否有效)分别为总票数的69%、63%、44%、58%和56%。问本次投票的有效率最高可能为多少?( )

A.65% B.70% C.75% D.80%

【解析】不妨设参与投票的观众总人数为100人，则5幅作品的得票数(不考虑是否有效)分别为69、63、44、58和56，这几个数字的和为290，即5幅作品的总得票数为290，而总共有100人参与投票，可根据等量关系列式求解，投票情况分为有效票和无效票，其中投1幅或2幅作品的票为有效票，投3幅或4幅或5幅作品的票为无效票，设有效票为x，无效票为y，可列出等式：x+y=100和(1，2)x+(3，4，5)y=290。根据 “小系数，同方向”，x的系数(1，2)比y的系数(3，4，5)要小，所以x与y的系数选择与x的极值取值方向一致。题目要求投票的有效率最高，即有效票数x最大，所以x与y的系数分别取系数范围中的最大值，x的系数取2，y的系数取5，由此得到2x+5y=290，再结合x+y=100，通过简单的代入消元即可确定x=70，所以有效票最多为70票，而此时总投票人数设为了100人，即投票的有效率为70%。选择B选项。

以上是“另类”和定最值问题解题技巧，希望大家勤做练习，熟练掌握，提高做题速度，增加答题准确率!

行测行程问题的“克星”——行程图

在公务员考试中，行程问题一直是热点也是我们考查的重点，考查的难度也往往是所有运算题型当中最难的一部分。因此行程问题是大部分考生最为头疼的一个题型，但是，任何题目都有技巧，只要摸准了这些题的规律，可以按照相同的思路去解决。那接下来我们就带大家来看看对于行程问题我们该运用什么样的思路来解决。

一.题型说明

行程问题主要研究的是路程s，速度v，时间t这三个量之间的关系，而且我们知道路程=速度×时间(s=v×t)。而在解决行程问题时候，很多的题目涉及到的主体和时间比较多，因此我们需要借助行程图来对题目中的行程过程进行梳理。

二.典型例题

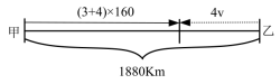
例1.甲、乙两地铁路线长1880千米，从甲地到乙地开出一辆动车，每小时行驶160千米，3小时后，从乙地到甲地开出一辆高铁，经4小时后与动车相遇，则高铁每小时行驶：

A.180千米 B.190千米 C.200千米 D.210千米

【答案】B

【解析】：设高铁速度为v千米/小时，从出发到相遇，动车行驶了(3+4)小时，高铁行驶了4小时。结合题意作图如下，根据图中线段关系可得(3+4)×160+4v=1880。解得v=190，因此答案选择B。

例2.甲、乙、丙三辆车的时速分别为60公里、50公里和40公里，甲从A地，乙和丙从B地同时出发相向而行，途中甲遇到乙后15分钟又遇到丙，问A、B两地相距多少公里?

A.150 B.250 C.275 D.325

【答案】C

【解析】：设甲和乙从出发至相遇用时为t分钟，则甲与丙从出发至相遇用时为(t+15)分钟。结合题意作图如下：

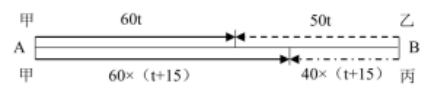
根据图中线段关系可得，60t+50t=60(t+15)+40(t+15)，解得t=150，即甲乙从出发至相遇用时为150分钟=2.5小时，则所求为60×2.5+50×2.5=275公里。

例3.甲、乙两人同时驾车从A地向B地出发，甲的车速是每小时50千米，乙的车速是每小时60千米，乙到达B地后立即原路返回，又过20分钟与甲相遇。A地与B地之间的距离是( )千米。

A.180 B.200 C.220 D.240

【答案】C

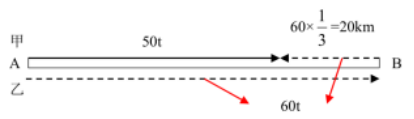
【解析】：假设甲乙经过t小时相遇，结合题意作图如下，根据图中线段关系可得50t+20=60t-20，解得t=4，则AB两地之间的距离为50×4+20=220千米。

通过上述的讲解，相信同学们能够对于行程图以及行程问题这一部分有很好的掌握，对于题目也知道该如何应对了，希望同学们能够在考试中从容应对此类型的题目，并且将这一部分的分数拿到手。

数量关系中等量关系的建立

在国家公务员行测考试中，有部分题目是可以通过列方程，建立等量关系来求解的。而在做题时如何去挖掘出题目中的等量关系呢?那么需要各位同学追根溯源从题干条件中获取，今天我们就带大家学习一下如何快速寻找这些等量关系。

一、典型例题

【例1】甲，乙两个工程队修公路，甲工程队修500米后由乙工程队来修，由以往资料显示乙工程队的效率是甲工程队的两倍，乙工程队修600米的时间比甲工程队修500米的时间少20天，甲工程队的工作效率为()米/天。

A.20 B.15 C.10 D.25

【解析】C。此题中出现“乙工程队修600米的时间比甲工程队修500米的时间少20天”可以推出：甲工程队修500米所用时间-乙工程队修600米所用时间=20天。设甲工程队工作效率为x米/天，则乙工程队工作效率为2x米/天，有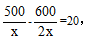解得x=10，故选C。

【例2】小明和爷爷在做数学游戏，小明说：“我比弟弟大10岁，而且我比爷爷小我年龄的4倍”，爷爷和小明的年龄的总和是弟弟年龄的18倍，问爷爷与弟弟年龄之和比小明年龄大多少岁?

A.65 B.60 C.62 D.58

【解析】A。此题中出现“爷爷和小明的总和是弟弟年龄的18倍”可以推出：爷爷的年龄+小明的年龄=弟弟的年龄×18，设小明的年龄为x岁，则弟弟的年龄为x-10岁，爷爷的年龄为5x岁，有5x+x=18×(x-10)，解得x=15。所求为5x+(x-10)-x=3x-10=65，故选A。

二、方法总结

我们根据第一题“乙工程队修600米的时间比甲工程队修500米的时间少20天”来建立等量关系，题干中出现“少”这个字，那么可以推出这是一个两者做差的等量关系，此类型的题目还有很多，列式可分为以下三种：

1，减法型列式：“A比B多(少)”，列式为A-B=C

2，加法型列式：“A与B共多少”，可列式为A+B=C

3，乘除型列式：“A是B的多少倍”，列式为A=-B×C或者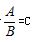

当然，在我们国考中各位同学还是需要根据具体题型具体分析，深层次挖掘题中的等量关系。希望本次的分享对同学们会有所帮助。

空瓶换水里的数学思维

行测数量关系在笔试中如何达到在最短的时间得到尽可能多的成效，缺少不了巧解题目的数学思维。空瓶换水属于统筹问题当中的一种，题目特征明显，属于数量关系里我们可以优先识别出来的题目。空瓶换水的题目理解起来并不困难，对于替换关系比较简单、题干中涉及到的数字较小的题目，确实可以按部就班的逐次分析。但是题目描述复杂、涉及的数字很大的题目，再去逐个分析确实没有这个必要。那么这次我们带大家一起看学一学空瓶换水里的数学思维。

【例题1】某商店节日促销，以“回收环保，以3换1”的主题售卖饮料。具体规定如下：3个同款饮料空瓶可以免费换1瓶同款饮料。一瓶饮料售价5元。李红现有30元，最多可以喝到几瓶饮料?

A.9 B.8 C.6 D.10

【解析】答案：A

易错点：李红首先可以用30元买6瓶饮料，喝完饮料以后得到6个空瓶。这6个空瓶还可以换2瓶饮料，再喝完会剩下2个空瓶，不满足“以3换1”的条件。所以一共可以喝到8瓶饮料。选择B项。但这并不是最优方案，为什么呢?

思路一：其实大家忽略了一种情况，李红可以先问商店“借”1个空瓶，这样加上之前剩下的2个空瓶，就凑够了3个空瓶，再去换一瓶饮料喝掉，最后把喝掉剩下的空瓶还给商店，能够达到“借1还1”的状态。这种数学思维能够达到最多喝9瓶饮料的结果。选择A项。

思路二：思路一可以达到最多的情况，但是只限数值较小的题目，如果这道题变成李红有100元，甚至更多钱，一点一点的推理会非常耗费时间，同时还需要考虑剩下的瓶子、换了以后的瓶子、借瓶子的情况等等。所以接下来的方法才是大家学习的重点。

最终我们需要的是最多能喝多少瓶饮料，所以可以从替换关系入手分析。3个空瓶=1瓶饮料→3个空瓶=1个空瓶+1份饮料(没有瓶子装的饮料)→2个空瓶=1份饮料。这样的替换关系就可以忽略再次换饮料以后还会留下空瓶的过程。现在李红有30元，可以先买30÷5=6瓶饮料，得到6份饮料和6个空瓶，替换关系为2个空瓶=1份饮料，所以其中的6个空瓶=3份饮料，最终最多可以喝到6+3=9份饮料。选择A项。

【例题2】某商店节日促销，以“回收环保，以5换1”的主题售卖饮料。具体规定如下：5个同款饮料空瓶可以免费换1瓶同款饮料。一瓶饮料售价5元。李红现有100元，最多可以喝到几瓶饮料?

A.20 B.24 C.25 D.26

【解析】答案：C

5个空瓶=1瓶饮料→5个空瓶=1个空瓶+1份饮料(没有瓶子装的饮料)→4个空瓶=1份饮料。现在李红有100元，可以先买100÷5=20瓶饮料，得到20份饮料和20个空瓶，替换关系为4个空瓶=1份饮料，所以其中的20个空瓶=5份饮料，最终最多可以喝到20+5=25份饮料。选择C项。

大家一定要多加练习，熟知各类问题当中体现出的数学思维。空瓶换水不再难!数量关系节节高!