特征数字法

在公务员考试中行测中的资料分析部分，由于给定的材料一般都来源于一些分析报告或者是行业统计，因此数据往往是比较大的，计算时如果要精算是非常困难的。所以在资料分析考试中就成了我们广大考生最大的难题之一。而面对如此复杂的数据计算，我们只有采取估算的方法去估算结果，才能在考试中节省更多的时间，今天教大家一种小技巧，叫特征数字法。

一.什么是特征数字法

利用百分数和分数之间的转化，将百分数近似转化为一些特定分数，从而达到简化计算的目的，称为特征数字法。

二.应用

任何含有百分数的列式都有可能用特征数字法进行计算。

三.例题

例1.2864×25%=

A.655 B.683 C.716 D.759

【答案】C。解析：由于式子中含有百分数25%，因此可以考虑将百分数25%转化成分数。因此选C。

例2.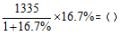

A.174　　　 B.182　　 　C.191　　 　D.198

【答案】C。解析：由于式子中含有百分数16.7%，因此可以考虑将百分数16.7%转化成分数。因此选C。

例3.中关村上市公司协会公布的《2016年中关村上市公司竞争力报告》显示，2015年，中关村上市公司总营业收入达到2.34万亿元，同比增长19.8%。截至2015年底，中关村上市公司总市值达到48175亿元，同比增幅54%，较2011年增长了约34824亿元。

问题：2015年与2014年相比，中关村上市公司总营业收入增加了()。

A.0.64万亿元 B.0.51万亿元 C.0.39万亿元 D.0.28万亿元

【答案】C。解析：根据文字“2015年中关村上市公司总营业收入达到2.34万亿元，同比增长19.8%”可知，总营业收入2015年比2014年增加了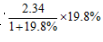万亿元。由于式子中含有百分数19.8%，因此可以考虑将百分数19.8%转化成分数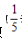去计算，则式子可以变为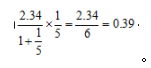。因此选C。

以上就是关于特征数字法使用的讲解，希望同学们下去之后抽空可以自己把我们考试经常用到的一些百分数与分数的转化找出来并且记得滚瓜烂熟，并且在平时的计算学习中一定要多应用，只有用的熟练了，才能在考试中提高我们的计算速度，为我们的考试节省大把的时间!

精确计算别犯愁

在资料分析中，有些题目是通过简单计算或者是使用一定的计算方法就能够快速得到答案。但同样也存在一部分题目，由于选项差距较小，需要精确计算以保证答案的准确性。很多考生对于这部分题目表示很头疼，所以今天跟大家分享一个计算技巧为大家“解忧”。

一、典型例题

例1.截止2018年年底，中国人工智能市场规模约为238.2亿元，同比增长率达到56.6%。从中国人工智能企业地域分布情况来看，北京企业数量最多，企业数量为368家;其次为广东，人工智能企业数量为185家;排名第三的是上海，数量为131家。

【问题】：若按照2018年的同比增长率，到2019年年底中国人工智能市场规模约为：

A.373亿元 B.371亿元 C.363亿元 D.383亿元

【答案】A。解析：根据材料可知，截至2018年年底，中国人工智能市场规模约为238.2亿元，同比增长率达到56.6%。按照2018年的同比增长率，2019年年底中国人工智能市场规模约为238.2×(1+56.6%)≈238×1.57=373.X亿元，选择最接近的A项。

【小结】这道题的关键点在于所列式子的计算，如果想粗略估算很容易出现错误。因为A和B的选项差距比较小，所以计算时要精确一些。如果我们采取三位乘三位的方式去计算，运算量还是略微大一些。此时，我们可以采取运算的拆分简化运算过程。

二、方法简介

所谓运算的拆分，就是把复杂的百分数拆分为整十或整五等便于计算的百分数进而达到简化运算的目的。

例如刚才的例题如果采取运算的拆分，则可按照如下的方式计算238.2×(1+56.6%)>238.2×(1+50%+5%+1%)=238.2+119.1+11.91+2.382≈371.X，最终选择比371.X大的选项即可，答案仍选A。

三、巩固训练

例2.2016年某市一次有关市民邻里关系的调查显示：在受访的951位市民中，“没有邻居”的有6位。“有邻居”的受访市民中，对邻居表示“了解”的占55.8%，其余的表示“不了解”;对邻里关系表示“满意”的占88.4%，“不满意”的占7.8%，其余不愿意表态。

【问题】：有531位受访市民“了解”邻居。(判断正误)

【答案】错误。解析：受访市民中“了解”邻居的有(951-6)×55.8%=945×55.8%<945×(50%+5%+1%)=472.5+47.25+9.45≈529，“了解”邻居的人数小于531人，则题干表述错误。

【小结】这道题是对于运算拆分的巩固训练，其实在拆分的过程中除了可以拆分成如50%、20%、10%这种常见的百分数之外，像14.3%≈、11.1%≈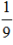这类大家不熟悉的百分数，大家在平时做题的时候也可以自己多去总结。这样，能拆分的形式就更加灵活，运算也会更加简便。

其实，行测资料分析的解题速度，不仅与阅读能力以及公式掌握熟练度有关。很多时候，还和计算方法的选择有关。所以，建议大家可以平时多去练习，多去探讨这类简便的计算方法。

行测资料分析概念篇——年均增长

行政职业能力测试一直是公务员考试的科目，包括言语理解与表达、数量关系、判断推理、常识和资料分析五大部门。而资料分析是考试中比较容易拿分的一个部分，因此备考的性价比是很高的。在资料分析备考中，我们首先要做的就是掌握所有的考点，熟练列式。今天带大家一起学习年均增长的相关考点。

1.求年均增长量

年均增长量=(其中n为年均增长次数)

例1，2016-2019年，我国焦炭生产量分别为44911.48万吨、43142.55万吨、44834.2万吨、47126.16万吨。则2016-2019年我国焦炭生产量年均增长量是多少万吨?

【解析】2019年的值为末期值，2016年的值为初期值，所求年均增长量

===

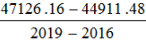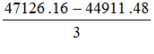
2.求年均增长率

年均增长率=

(其中n为年均增长次数)

例2，2016-2019年，我国焦炭生产量分别为44911.48万吨、43142.55万吨、44834.2万吨、47126.16万吨。则2016-2019年我国焦炭生产量年均增长率是多少?

【解析】2019年的值为末期值，2016年的值为初期值，所求年均增长率

==

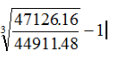
3.求末期值

末期值=初期値+n×年均增长量=初期值×(其中n为年均增长次数)

例3，2009年我国建筑业总产值76807.74亿元，2009-2014年平均每年增加19981亿元。则2014年，我国建筑业总产值为多少亿元?

【解析】末期值=初期値+n年均增长量=76807.74+5×19981

4.求初期值

初期値=末期值-n×年均增长量=(其中n为年均增长次数)

例4，2014年，我国国有控股企业法人单位数有263348个，与四年前相比实现每年约3431.5 个的增长。则2010年，我国国有控股企业法人单位约有多少个?

【解析】初期値=末期值-n×年均增长量=263348-4×3431.5

年均增长的考点和公式我们就学习到这里，大家一定要熟练记忆所有公式，这是资料分析备考的第一步。。

巧解资料分析之增长量

在行测考试中，资料分析一直都是一种比较常见的题型，也是我们必做的一个专项，因为它能够通过学习复习，在短时间内得到提高，正确率在80%以上是非常常见的。但是在复习的过程中，当我们掌握了资料分析的各种公式之后，我相信有很大一部分考生都有同样的感受：基本上每个题都知道该怎么列式，但因为计算比较复杂耽误时间导致做题速度慢，或是去计算，但是算错了。由此可见计算技巧的重要性。那么今天给大家带来一种常见题型的计算技巧——增长量的计算。

增长量，也就是现期量与基期量的差。但是在考试中一般不会以这种求差的形式考查，最常考查的增长量题型是告诉我们现期量A和增长率q，增长量。从式子中就可以看出，增长量的公式比较复杂，分子为两个数的乘积，也就是做乘法后还需要做除法才能得出结果，若按常规方法计算，较为复杂。现在此给大家介绍一种比较简单易操作的增长量的计算技巧。

首先，观察q，看增长率这个百分数与几分之一比较接近，也就是将q看成与之近似的1/n，用1/n来代替q带入到公式中，此时增长量的公式可以进一步化简为增长量。最后，只需要做一个简单的直除即可得到答案。

例1.2011年上半年，嵌入式系统软件实现收入1443亿元，同比增长33.8%，增速比去年同期高14.2个百分点。求2011年上半年嵌入式系统软件收入同比增长了多少亿元?

A.307 B.365 C.424 D.488

【答案】B。解析：先判断题型，通过提问“同比增长了多少亿元”，可以判断是求增长量，再看题干是“2011年上半年同比”，即可知道2011年上半年为现期，则现期量为1443亿元，增长率为33.8%，33.8%≈1/3即n≈3，所以将其带入公式增长量=A/(1+n)≈1443/(1+3)=360.75亿元，则选择最接近的B项。

例2.2010年一季度，我国水产品贸易进出口总量158.7万吨，进出口总额40.9亿美元，同比分别增长14.2%和29.0%.其中出口量67.1万吨，出口额26.5亿美元，同比分别增长11.7%和24.9%;进口量91.6万吨，进口额14.4亿美元，同比分别增上16.0%和37.5%。2010年一季度，我国水产品出口额比上年同期约增长了多少亿美元?

 A.5.3      B.7.0  C.9.2        D.21.2 

【答案】A。解析：由题意知，本题所求的是2010年一季度的同比增长量，而材料中所给的是2010年一季度的现期量26.5亿美元和增长率24.9%，第一步，先把增长率化成分数：24.9%≈1/4，即n≈4，所以将其带入公式增长量=A/(1+n)≈26.5/(1+4)=5.3亿元，则选择A项。

通过刚才的计算过程可以看出，想要快速计算增长量的话需要记住一些常见的1/n的百分数形式。即：

1/2=50% 1/3=33.3% 1/4=25% 1/5=20% 1/6=16.7% 1/7=14.3%

1/8=12.5% 1/9=11.1% 1/10=10% 1/11=9.1% 1/12=8.3% 1/13=7.7%

1/14=7.1% 1/15=6.7%