政华教育

参考解析：题干需要求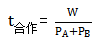, 而题干中工作量与效率并不知道，但是我们可以结合题干信息用工作量表示每个车间的效率，即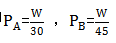,所以将两个车间的效率带入上式即可得到分子与分母的工作量约分掉，所以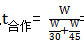=18天，所以通过分析我们可以发现即使工作量未知，但是不影响计算，所以后期为了简化计算我们即可以用特值法：找到题干中已知单独完成工作的时间的最小公倍数为工作量的特值，直接带入计算即可快速解题，所以本题设工作量W=90(30天和45天的最小公倍数)，所以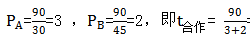=18天。

【例2】随着我国国力的提升，我国的工农业得到了大力的发展，就以纺织业的原料为例，新疆的棉花产业为我们的纺织业做出了巨大的贡献，现在在机械化生产的过程中，某农户2020年在收割棉花的过程中，如果使用5台大型收割机可15天收割完成，如果用6台小收割机则25天即可完成，现在由于天气原因需要加紧收割，如果同时使用5台大型和4台小型收割机同时收割需要几天?

A.14 B. 12 C. 11 D. 10

参考解析：结合题干已知大型和小型收割机单独完成时间，则可设棉花产量的工作量为：W=75(25和15的最小公倍数)，所以每台大型收割机效率为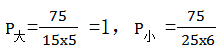=0.5，所以如果同时使用需要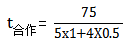= 10.x天，所以取11天。

通过以上两个例题为大家主要介绍了工程问题中如何能够使用特值法快速解题，在使用最小公倍数时结合题目判断题目已知的是单独完成的时间，即可快速找到时间最小公倍数为工作量的特值，此时将该工作量作为已知条件带入题干即可计算效率和时间。

“六字诀”解“另类”和定最值

和定最值问题在近几年的公考当中可谓“常客”，特别是在国考和省考当中出现了一种“另类”的和定最值问题，这种问题让考生头疼不已，但是对于这种问题我们其实只用掌握他的套路也可以在考试当中轻松拿分，接下来一起去了解一下这种问题应该如何解决。

另类和定最值

例：书法大赛的观众对5幅作品进行不记名投票。每张选票都可以选择5幅作品中的任意一幅或多幅，但只有在选择不超过2幅作品时才为有效票。5幅作品的得票数(不考虑是否有效)分别为总票数的69%、63%、44%、58%和 56%。则本次投票的有效率最高可能为多少?

A.65% B.70% C.75% D.80%

【答案】B。参考解析：不妨设参与投票的观众总人数为100人，则5幅作品的得票数(不考虑是否有效)分别为69、63、44、58和56，则我们就可以得到5幅作品的总得票数为290，而总共有100人参与投票，就有明显的等量关系，有效的和无效的投票总数应该为290。可根据等量关系列式求解，投票情况分为有效票和无效票，其中投1幅或2幅作品的票为有效票，投3幅或4幅或5幅作品的票为无效票，设有效票数量为x，则无效票为100-x，可列出等式：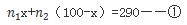

(注意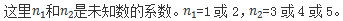：因为题目未直接给出，需要我们判断。)

那如何确定列式当中x和100-x的系数是解方程的关键。对式子作以整理化简。得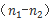

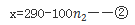
(这里我们注意所以②式可以写为

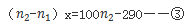
这样两边都是正值直接可以判断取值，由题目得x取最大值，也取最大值。即原来①为2x+5(100-x)=290，解的x=70，即有效率为70%。故本题选择B项。

刚才给大家已经介绍了具体思路，要想求解方程，需确定方程中未知项的系数分别为多少，在这里，我们为大家介绍一个小技巧：“小系数，同方向”，即未知数的系数的选择与小系数对应的未知数的极值取值方向一致。例如本题x的系数(1,2)比100-x的系数(3,4,5)要小，所以x与100-x的系数选择与x的极值取值方向一致。题目要求有效率最高，所以x与100-x的系数分别取系数范围中的最大值，x的系数取2，100-x的系数取5，由此得到2x+5(100-x)=290，解的x=70。即有效率为70%。故本题选择B项。

小结

“小系数，同方向”，即未知数的系数的选择与小系数对应的未知数的极值取值方向一致。考生只要对这“六字诀”理解清楚并且知道如何操作，那么在考试当中即使出现这种问题也可以直接拿分，是不是很简单呢。

和定最值之逆向极值与混合极值

和定最值是数量关系中比较常考、也是比较容易拿分的题型，因为它的做题方法和其他直接找等量关系的题型不同，知识系统也相对独立。前边我们已经讲了同向极值，接下里我们就讲一讲另外两种模型：逆向极值和混合极值。我们只要熟记它的题目特征和解题原则就能很轻松地予以解决。

逆向极值题型特征：已知几个数的和，求其中最大量的最小值或者求最小量的最大值。

混合极值题型特征：已知几个数的和，求中间某个量的最大值或最小值

解题原则：求其中某个量的最大(小)值，让其他的量尽可能的小(大)。

这种题型需要满足：

1)已知几个数的和(有时可能会告诉平均数)

2)求其中某个量的最大值或者最小值

下面我们根据几道简单的例题来理解一下和定最值中逆向极值的解题方法。

【例1】有4支队伍进行4项比赛,每项比赛的第一、第二、第三、第四名分别得到5、3、2、1分。每队的4项比赛得分之和算作总分,如果已知各队的总分不相同,并且A队获得了三项比赛的第一名，问总分最少的队伍最多得多少分?

A.7 B.8 C.9 D.10

【参考解析】B。4支队伍的总分为4×(5+3+2+1)=44分，要使总分最少的队拿最多的分，则其余队的分数要尽量少，其中A队最少拿5×3+1=16分，即剩余三个队最多拿44-16=28分，设总分最少的队伍最多得x分，其余队的分数最少依次为x+1、x+2分，依题意有x+x+1+x+2=28,解得x=8.X，x为不大于8.X的整数，故总分最少的队伍最多得8分。

【例2】舞蹈队的年龄之和是2654岁，其中年龄最大的不超过79岁，最小的不低于50岁，且最多有4个人彼此年龄相同，则这些人中至少有多少人的年龄不低于60岁?

A.5 B.6 C.7 D.8

【参考解析】A。根据题意，低于60岁的人的年龄和最多为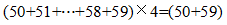×20=2180，则不低于60岁的人年龄和为2654-2180=474,要使年龄不低于60岁的人最少，则应使年龄和为474的人年龄尽可能大，474=79×6，即最多有4个人彼此年龄相同，故这些人中至少有7人的年龄不低于60岁。

【例3】将21个苹果分给5个人，每个人分到的苹果数各不相同，问分到苹果第二多的人最多分几个?

A.7 B.8 C.9 D.10

【参考解析】A。此题满足和定最值的题型特征，想要第二多分得最多，那就让其他的尽可能的小，排名后三的分别为1、2、3，此时剩下15个苹果，设第二多分得x个，那么分得最多的人最少分x+1个，则共2x+1=15，x=7，因此选择A。

以上基本上就是所有可能在和定最值中逆向极值和混合极值的出题方式和解题方法了，希望考生们能够通过这几道例题来掌握此种题型的解题思路，根据不同的出题方式都能找到相应的解题方法。

增长率你真的学会了吗

资料分析考查考生对于材料和题干的分析能力，对于考点所涉及公式的熟练把握以及对所列式子的计算能力。其中增长是资料分析中的核心考点，考试考查较为全面。然而关于增长的考点，很多同学仍然存在盲区，今天带大家来学习增长中的一个重要考点——增长率。

一、含义

增长率：现期值相对基期值增长的百分比。

增长量：现期值对基期值增长的量。

很多同学初学资料分析的时候，很容易混淆增长量和增长率这两个概念。到底如何区分这两个考点，我们需要记住增长+单位，考查增长量;增长+百分数，考查增长率;增长之后什么都没有加，我们需要结合选项来判断。

二、计算公式

【例1】2018年全国粮食产量65790万吨，2019年粮食产量比上年增加594万吨。

问题：2019年全国粮食产量比上年增长百分之几?

【参考解析】所求为增长+百分之几，考查增长率。材料中给到基期值和增长量，因此

【例2】2019年国内生产总值990865亿元，2018年国内生产总值为919281亿元。

问题：2019年国内生产总值比2018年增加了百分之几?

【参考解析】所求为增长+百分之几，考查增长率。材料中给到现期值和基期值，因此

三、混合增长率

混合增长率介于各部分增长率之间。

【例1】2014年全国社会物流总额213.5万亿元，同比增长7.9%，其中上半年101.5万亿元，同比增长8.7%。

问题：2014年下半年社会物流总额比上年同期增长百分之几?

A.7.2% B.8.0% C.8.6% D.9.3%

【参考解析】所求为增长+百分之几，考查增长率。材料中给到2014年同比增长率7.9%，2014年上半年同比增长8.7%，根据2014年下半年的增长率<2014年的增长率<2014年上半年的增长率，所求2014年下半年的增长率<7.9%，选择A选项。

对于增长率，同学们除了需要学会识别考点、掌握基本公式，还需了解混合增长率的考法。期待跟同学们分享更多资料分析的考点和解题技巧，希望大家学有所成!