在行测题目中，我们经常为立体图形中的折纸盒题目发愁，今天给大家讲解顶点法，解决折纸盒题目，不再举步维艰!下面放一道简单题目，旨在帮助大家理解顶点法。
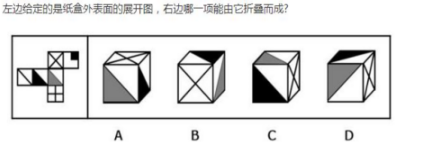
折纸盒题目，第一步永远是相对面排除法，想必小伙伴们对于怎么找相对面已经很清晰了，这道题也不能用相对面排除选项，我们就直接进行下一步吧!
第二步使用顶点法，顶点法的理论部分确实看起来有些复杂，要耐心看完，以后使用起来会非常方便的!
顶法的理论，一共分为三步：
1. 确定顶点：在平面展开图中，连接三个面的点是确定顶点。
2.顶点法：在平面展开图外围，与确定顶点距离为“1”的点是同一个点。
第一步：标现有确定顶点，即连接三个面的点，有几个标几个
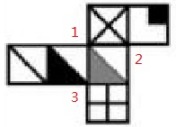
第二步：123的两侧依次标点：1两边标4，2两边标5，3两边标6
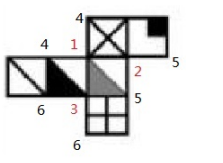
第三步：补齐剩余点：我们看到4，现在一共有两个4，这两个4一共连接了三个面，所以4也是一个确定顶点，可以使用顶点法。在平面展开图外围，与确定顶点4距离为“1”的点是同一个点，我们刚刚根据1找到的4，不能再标1，这时发现两个4两边的点都是空的，没有命名，故命名下一个数字7.
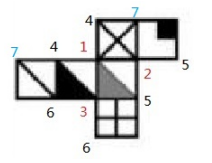
两个7一共连接了三个面，是确定顶点，两边标8。
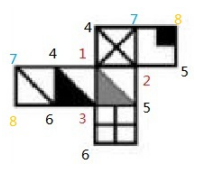
两个8只连了两个面，在最后的右下角标上第三个8，此时每个数字都连接了三个面，标齐正确。
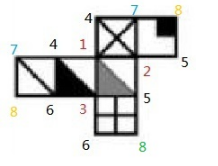
此时我们看到，题目每个选项都是要两个三角形和×这三个面相连的关系，根据刚刚标的点，是1连接了这三个面，所以应该在黑三角图中位置方向的右上角，灰色三角图中位置的左上角，×面的任意位置，根据这三个位置锁定答案D。
实际做题的时候我们也可以根据一个面确定是哪个顶点，看另外两个面相对位置都对不对，也可以像这道题，看三个面确定是哪个点，灵活运用，希望各位小伙伴能真的掌握顶点法，稳稳的做对这道题!
如何快速解决错位重排问题
在行测考试中，排列组合问题一直是同学们比较头疼的一类问题，然而在排列组合问题中有这么一类题型是看似很难，但一旦有了抓手就会变成非常得心应手，那就是错位重排问题。这个数学模型是伯努利和欧拉在错装信封时发现的，因此又称伯努利-欧拉装错信封问题。接下来为大家详细介绍：
首先我们先来理解一下什么是错位重排：错位重排是指把n个元素的位置重新排列，使每个元素都不在原来位置上的排列问题。我们可以形象的理解为：“某个人写了n封信，以及n个带有地址的信封，求所有信件全部装错信封的情况数。”用一句话简单描述就是元素和位置的对应关系要重新排列且不能恢复原本的位置关系。那么接下来我们一起具象化一下这个数学模型：将编号1、2、3……n的n封信分别装入编号为1、2、3……n的n个信封，要求每个信封和信的编号不同，问共有几种装法?
对于这道题目中涉及到的元素数也就是信封的个数我们用字母n来表示，而所要求得的方法数我们用字母Dn来表示，因为题干要求信与信封编号不能相同，由此我们判定这是一道错位重排类型的题目。那么对于错位重排问题我们只需要记住下边这个表格，会从题干中找到错位重排的元素个数，这种问题就可以轻而易举地做出来了。
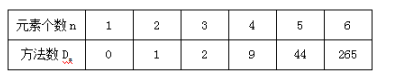
例.编号1、2、3、4、5的五封信分别装入编号为1、2、3、4、5的五个信封，要求有且只有一个信封和信的编号相同，问共有多少种装法?
A.43 B.44 C.45 D.46
【答案】C。解析：题干中只有一个信封和信的编号相同，也就是说剩余的四个信封和信的编号都不同，属于错位重排问题。题干中有五封信，具体哪封信和编号相同我们不得而知，所以我们先考虑从五封信中挑选一封让它和它的编号相同，有
种情况;再考虑剩余四个信封和信编号不同的情况数，为基本的错位重排，有种情况。因此满足条件的情况数有5×9=45种。选C。
各位同学在以后的做题中，一旦发现题干要求元素与对应位置不相同时，就要快速甄别出这类题型是错位重排问题。除此之外你还需要记住上面表格的常考数据。一般情况下大家记住D1-D5所对应的数据即可应对绝大多数考试题目。
脚尖旋转，阴影自开
公务员考试中数量关系这类题型是大家公认的比较难的题型，主要是因为知识点比较多，时间不够用，跟其他题型相比性价比没有那么高，因此实战的原则就是挑题做捡题做，几何问题就属于大家可以挑的题型之一，考察的知识点相对比较明确，主要考察平面几何和立体几何，其中平面几何以常见几何图形的周长和面积为主要考察对象，求面积的题型中阴影部分面积的求解是不少同学的难点，其实对于阴影部分面积的求解，只要用对方法大家就会发现没有那么难，所谓“脚尖旋转，阴影自开”，今天就带大家看看如何使用旋转法解决阴影部分面积。
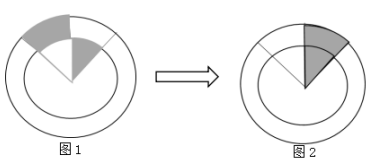
求阴影部分面积看似复杂，稍作旋转就会有“山重水复疑无路，柳暗花明又一村”的既视感，如图1，图中阴影有两部分，其中一个属于不规则图形，单独求出每部分的面积之后再相加就有些复杂了。如果我们把图中不规则的部分稍作旋转，变成图2，两部分阴影合成一个，就是我们熟悉的扇形，再利用扇形的面积求解公式直接求解即可。旋转一下，化繁为简，是不是很神奇了?
【例题1】如图，一个边长为4cm的正方形，内部放了四个与正方形相切的圆，且圆两两相切，求图中阴影部分的面积?
A.4 B.6 C.8 D.10
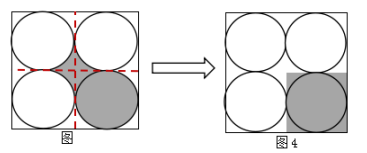
【解析】答案：A。如图，图中阴影包含两个部分，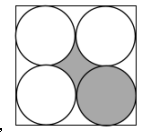
一部分是内部小圆的面积，一部分是四个圆中间形成的阴影部分面积，单独求解四个圆中间形成的阴影部分面积不好求解，可连接正方形四边的中点，因四个圆两两相切，则中线必过切点且与正方形的边形成四个边长为2cm的小正方形，且每个圆均与小正方形相切(如图)，此时中间阴影部分被分成四个面积相等的小部分，再将四个小阴影部分稍作旋转，均放在一个小正方形中(如图4)，此时阴影部分的面积就变成小正方形的面积2×2=4(cm2)，故答案选A。
【例题2】如图，太极八卦图外部是以O点为圆心，6cm为半径的圆，其内部白色小圆与黑色小圆的圆心与大圆圆心在同一条直线上，且小圆直径为2cm，求图中阴影部分的面积?
A.8π B. 12π C. 16π D.18π
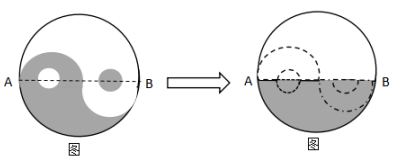
【解析】答案：D。如图，阴影部分分为两块，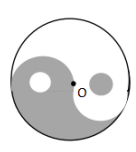
一块为小圆的面积，一块为不规则图形的面积，不规则图形的面积单独求解不好求，可以做如下处理,过O点连接白色黑色两个小圆的圆心并延长交大圆于A、B两点(如图)，将黑色小圆向左移动与白色小圆重合，再将直径AB上方形成的新的阴影面积向右旋转180°(如图6)，此时阴影部分面积就转化为半圆的面积即S阴=π62÷2=18π(cm2),故选择D。
【例题3】如图，等腰直角三角形，斜边为6cm，在两直角边上取一定长度为直径作两个半圆，且两半圆相切，分别与等腰三角形的斜边截得长度为2cm、3cm的弦，求阴影部分的面积?
A.2 B. 2.5 C. 3 D.3.5
【解析】答案：B。如图，阴影包含三个部分，两个弧形，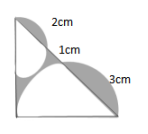
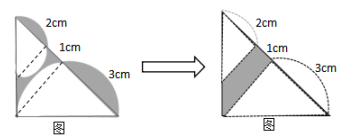
一个不规则的部分，分别连接两半圆与等腰三角形两边的交点(如图)，根据直径对应的圆周角是90°，可得两虚线垂直于斜边且相互平行，又因为大三角形是等腰三角形，则两个小三角形也是等腰三角形，所以外部两个弧形阴影的面积与内部两个弧形的面积相等，故将外部大小两弧形阴影分别向左、右旋转90°(如图8),阴影部分面积就转化成了梯形的面积，所以梯形面积为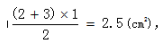
故答案选择B。
综上，阴影部分面积的求解是不是没有大家想的那么难了?“脚尖旋转，阴影自开”你还在等什么呢?跟着一块学习吧。
