几何问题可以说是公务员行测考试中的重要题型，其涉及的考点也比较多，如平面图形的周长、面积，立体图形中的表面积、体积，相似，计算最短距离，方位角等等，在这些考点中，关于直角三角形的相关考点可以说一直是热门，经常出现在各大考试当中，今天，为各位考生深入剖析几何问题中的直角三角形。

一、基础知识

对于直角三角形，两直角边分别为 a，b，斜边为 c，满足勾股定理：。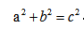

常见的勾股数有 3、4、5;5、12、13。同时，勾股数可以等比例扩大，如 3、4、5 可以扩大为6、8、10。

要掌握含 30°和 45°角的两个特殊直角三角形三边的比例关系。在直角三角形中，若有一个角为30°，则三边的比例关系是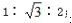; 若有一个角为 45°，则三边的比例关系是。

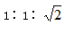二、考点精练

例1：文化广场举行放风筝比赛，老年组老王、老侯、老黄三位选手同场竞技，评委测量各人放出的风筝线长分别为60米、50米、40米，风筝线与地平面所成的角分别为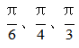，假设风筝线看作是拉直的，则三位选手放风筝最高的是?

A.老黄 B.老侯 C.老王 D.不能确定

【答案】B。解析：根据题意，老王的风筝与地面成30°，则风筝高与风筝线长之比为1:2，故风筝高度为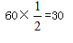，老侯的风筝与地面成45°，则风筝高与风筝线长之比为，老黄的风筝与地面成60°，则风筝高与风筝线长之比为，故老侯的风筝放的最高。

例2：甲、乙、丙、丁四人通过手机的位置共享，发现乙在甲正南方向 2千米处，丙在乙北偏西 60°方向 2 千米处，丁在甲北偏西 75°方向。若丁与甲、丙的距离相等，则该距离为：

【答案】B。解析：根据题干中四人的关系，可画图如下，连接A、C。在△ABC中，AB=BC=2 千米，∠B=60°，则△ABC 是等边三角形，那么 AC=2 千米，∠BAC=60°。在△ACD中，AD=CD，∠CAD=180°-60°-75°=45°，则△ACD 是等腰直角三角形，∠D=90°，那么 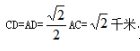千米。

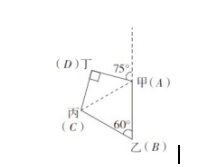
通过以上两道例题的分析不难发现，直角三角形的考查通常会结合生活实际去考查，考生做题时，需要养成边读题边画图的习惯，并善于做辅助线，将所求线段置于直角三角形里，再通过直角三角形的三边关系进行求解。

论分工的重要性之多劳力合作问题

在公务员考试中，多劳力合作问题是大家所不太熟悉的题型，也是难度系数相对大一些的题型，我们大多数同学可能会望而生畏，选择放弃。然而，我们只要理清题干条件，把握解题核心——分工问题，多劳力合作问题就变成我们所熟悉的普通工程问题。今天，就带大家一起来深入了解一下如何求解多劳力合作问题。

一、何为多劳力合作问题

多劳力合作问题是指已知多个人去做多项工作，而他们各自做这些工作的效率不同或者时间不同，最后求在时间一定的情况下的最大工作量或者是在工作量一定的情况下的最短时间。

二、多劳力合作问题的解题核心

其实，想要解决好多劳力合作问题，无非就是把握效率高这样一个核心。那么如何达到最高效率呢?合作是前提，然而分工是关键。在一个团队中，我们明白人力资源要优化配置，充分发挥自身的优势。那么在此类问题中也是如此，也就是令擅长的人或者队伍做擅长的工作。那么如何确定谁更擅长哪项工作呢?只要比较相对效率或者相对时间即可。

三、常考题型

在实际考试中，有的题目会已知效率，有的题目会已知时间，今天我们先学习已知效率的情况下如何解决多劳力合作。

【例题精讲】

甲乙两人共同加工A、B两种产品，已知甲每天加工20个A产品，10个B产品，乙每天加工15个A产品，12个B产品。现在要完成100个A产品和82个B产品的工作任务，最少需要多少天?

A.5 B.6 C.7 D.8

【解析】

首先，根据题干信息列出表格。

我们可以横向看，即甲做A、B两项工作的效率之比为20/10=2，乙做A、B两项工作的效率之比为15/12=1.25，说明甲少加工一个B，能多加工2个A;乙少加工一个B，能多加工1.25个A，所以甲更擅长做A工作，那么乙更擅长B工作。我们也可以纵向看，即对于A产品而言，甲乙效率之比为20/15=4/3，对于B产品而言，甲乙效率之比5/6，说明乙生产一个A的时间下，甲可以生产4/3个A，乙生产一个B的时间下，甲可以生产5/6个A，所以得到结论：甲更擅长做A工作，那么乙更擅长B工作。接下来开始合作即可。100个A产品，甲只需要100/20=5天。此时，乙只完成B产品(5×12)=60个，B产品剩下(82-60)=22个。最后甲乙合作生产22个B产品，所花时间为：22÷(10+12)=天。总时间为6天。故答案选择B项。

其实，细品多劳力合作问题不难发现，它比普通合作问题只是多了一步，那就是把工作合理分工的过程，这也就是我们的解题核心。只要我们列出表格，横向或者纵向得到比值，进行比较分析即可。

排列还是组合，你分的清么

在各类行测考试中，排列组合问题虽然整体题量不高，但经常会和诸如极值问题等题型混合考查，在概率问题中也会涉及到相关知识。而对于绝大多数考生而言，排列组合如同天堑，学习时选择性放弃、考试时战略性蒙题。出现这种情况，很重要的一个原因就是，很多人倒在了做题的第一步，这题到底是排列还是组合?所以我们首先要做的就是，学会如何判定元素间是排列关系还是组合关系。

【例1】某公司有A、B两个部门，各部门均有8名员工。公司决定派遣A部门中的两名员工去参加培训，共有( )种不同的派遣方式。

A.28 B. 42 C. 56 D. 63

【详解】A。对于这个问题我们应该用排列数还是组合数计算呢?判定的方法就是：改变元素的选取顺序，看对结果是否产生影响。如果有影响就应该用排列数，反之无影响，则用组合数计算。

第一问中要从A部门的8名员工里选择2名去总部。假如我们选取的两个人是甲和乙，此时我们会发现，改变选取的顺序：无论是先选甲后选乙，还是先选乙后选甲，最后都是甲和乙两人参训，改变顺序对结果并未产生影响，所以应该采用组合数运算，共有种派遣方式，故选A。

【例2】某公司有A、B两个部门，各部门均有8名员工。公司打算从B部门中选择两位员工分别担任部长和副部长，共有( )种不同的选择方式。

A.28 B. 42 C. 56 D. 63

【详解】C。这道题公司要从B部门的8名员工里选择2名分别担任正副部长。假如我们选取的两个人是丙和丁，此时我们会发现，改变选取的顺序：先选丙担任部长后选丁担任副部长，以及先选丁担任部长后选丙担任副部长，丙和丁的职位发生了变化，产生了不同的结果。即改变顺序对结果并产生了影响，根据上题所讲的判定方法，应该采用排列数运算，共有种派遣方式，故选C。

理清了排列和组合的差异，我们一起再来看一道题目。

【例3】一个项目组有6名员工，其中有正副组长各1人，现从中选4人完成四项不同的工作，每人完成一项工作，且正副组长有且仅有1人参加，共有( )种不同的安排方式。

A .16 B. 192 C. 240 D. 2480

【详解】B。题目要求我们从6名员工中选择4人分别完成四个不同的工作。

所以我们要先决定哪4个人参加工作：由于正副组长有且仅有一人参加，所以先从两个人里任选一人参加，由于只选一人，不需要考虑顺序，共有种选法;接下来再从四名普通员工中选择三人，这三人无论选择的顺序如何最终都是这三个人参加工作，所以改变顺序未对结果产生影响，采用组合数计算，有种选法。则共有2x4=8种选法。

再决定这4人分别参与哪项工作：相当于把这4个人全部选出来安排到四项工作中，由于工作并不相同，所以改变这4个人的顺序，工作安排就会发生变化，对结果产生了影响，因此要采用排列数计算，共种不同的安排。

综上第一步人员共有8种选法，第二步这四人共有24种安排，则总共有8x24=192种不同的安排方式。故选B

近些年各类考试的排列组合题目，整体难度有所下降，这也就意味着我们在遇到相对简单的题目时，并不需要过多的复杂思考，只要我们能够分清楚排列和组合的区别，就可以用相对短的时间完成这些题目的解答。

工程问题之交替合作

数量关系是公考行测中的必考部分，也是高分同学必争的一个部分。数量关系中有的题型是非常简单的，只要掌握了题型特征和解题方法，很快就可以做出来的，工程问题中的交替合作就属于这类题目，今天带着大家一起学习交替合作。

一、交替合作含义

交替合作是指多个人或事物完成某一项工程，在合作过程中这些对象都是按照一定的规律轮流工作，这个过程就叫交替合作。

例：一条隧道，甲单独挖要20天完成，乙单独挖要10天完成。如果甲先挖1天，然后乙接替甲挖1天，再由甲接替乙挖1天……两人如此交替工作。那么，挖完这条隧道共用多少天?

二、解题关键

确定最小循环周期，并确定最小循环周期内的工作量之和。

三、解题步骤

1、确定工作总量和各自的工作效率，一般题目不直接给出，通常可以用特值法;

2、确定最小循环周期并求出最小循环周期内的工作量之和;

3、求出周期数：;

4、确定整周期之外剩余工作量所用时间;

5、根据问题求解。

四、方法应用

例1：一条隧道，甲单独挖要20天完成，乙单独挖要10天完成。如果甲先挖1天，然后乙接替甲挖1天，再由甲接替乙挖1天……两人如此交替工作。那么，挖完这条隧道共用多少天?

A.13 B.13.5 C.14 D.15.5

解析：正确答案B

这是交替合作问题，根据解题步骤：

第一步：题干中给了甲乙单独完工时间，我们可以设工作总量为20(20和10的最小公倍数)，此时甲、乙的效率分别为1、2;

第二步：这里最小循环周期为2天(甲、乙各1天)，一个周期内的工作量为3(1+2);

第三步：周期数为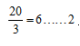：，也就是说需要6个周期还余2个工作量;

第四步：这2个工作量需要甲干1天，然后乙干0.5天;

第五步：问题求的是总时间，6个循环周期，每个周期2天，对应12天，再加上甲1天和乙0.5天，总共12+1+0.5=13.5，所以答案为B。

上面介绍的交替合作问题，大家学会了吗?接下来大家可以尝试自己做一下下面这个例题2。

例2：单独完成某项工程，甲需要16小时，乙需要12小时，如果按照甲、乙、甲、甲、乙、甲……的顺序轮流工作，每次1小时，那么完成这项工作需要多长时间?

A.13小时40分钟   B.13小时45分钟

C.14小时          D.14小时20分钟

解析：正确答案D，

这是交替合作问题，根据解题步骤：

第一步：题干中给了甲乙单独完工时间，我们可以设工作总量为48(16和12的最小公倍数)，此时甲、乙的效率分别为3、4;

第二步：这里最小循环周期为3小时(甲、乙、甲各1小时)，一个周期内的工作量为10(3+4+3)，

第三步：周期数为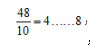：，也就是说需要4个周期还余8个工作量;

第四步：这8个工作量，甲1小时干3个工作量;乙1小时干4个工作量;剩余1个工作量，甲再需要干小时，即20分钟;

第五步：问题求的是总时间，4个循环周期，每个周期3小时，对应12小时，在加上剩余工作量甲总共干1小时20分钟和乙1小时，总共14小时20分钟，所以答案为D。