
一、工程问题
工作量=工作效率×工作时间;工作效率=工作量÷工作时间;
工作时间=工作量÷工作效率;总工作量=各分工作量之和;
注:在解决实际问题时,常设总工作量为1或最小公倍数
二、几何边端问题
(1)方阵问题:
1.实心方阵:方阵总人数=(最外层每边人数)²=(外圈人数÷4+1)²=N²
最外层人数=(最外层每边人数-1)×4
2.空心方阵:方阵总人数=(最外层每边人数)²-(最外层每边人数—2×层数)²=(最外层每边人数-层数)×层数×4=中空方阵的人数。
无论是方阵还是长方阵:相邻两圈的人数都满足:外圈比内圈多8人。
3.N边行每边有a人,则一共有N(a—1)人。
4.实心长方阵:总人数=M×N外圈人数=2M+2N-4
5.方阵:总人数=N2 N排N列外圈人数=4N-4
例:有一个3层的中空方阵,最外层有10人,问全阵有多少人?
解:(10-3)×3×4=84(人)
(2)排队型:假设队伍有N人,A排在第M位;则其前面有(M—1)人,后面有(N-M)人。
(3)爬楼型:从地面爬到第N层楼要爬(N-1)楼,从第N层爬到第M层要爬(M-N)层。
三、植树问题
线型棵数=总长/间隔+1环型棵数=总长/间隔楼间棵数=总长/间隔—1
(1)单边线形植树:棵数=总长¸间隔+1;总长=(棵数-1)×间隔
(2)单边环形植树:棵数=总长¸间隔;总长=棵数×间隔
(3)单边楼间植树:棵数=总长¸间隔-1;总长=(棵数+1)×间隔
(4)双边植树:相应单边植树问题所需棵数的2倍。
(5)剪绳问题:对折N次,从中剪M刀,则被剪成了(2ⁿ×M+1)段
四、行程问题
路程=速度×时间;平均速度=总路程÷总时间
(1)平均速度型:平均速度=2V₁V₂/V₁+V₂+
(2)相遇追及型:相遇问题:相遇距离=(大速度+小速度)×相遇时间追及问题:追击距离=(大速度—小速度)×追及时间
背离问题:背离距离=(大速度+小速度)×背离时间
(3)流水行船型:
顺水速度=船速+水速;逆水速度=船速-水速。
顺流行程=顺流速度×顺流时间=(船速+水速)×顺流时间
逆流行程=逆流速度×逆流时间=(船速—水速)×逆流时间
(4)火车过桥型:
列车在桥上的时间=(桥长-车长)÷列车速度
列车从开始上桥到完全下桥所用的时间=(桥长+车长)÷列车速度
列车速度=(桥长+车长)÷过桥时间
(5)环形运动型:
反向运动:环形周长=(大速度+小速度)×相遇时间
同向运动:环形周长=(大速度—小速度)×相遇时间
(6)扶梯上下型:
顺行:速度之和×时间=扶梯总长
逆行:速度之差×时间=扶梯总长
(7)队伍行进型:
对头→队尾:队伍长度=(u人+u队)×时间
队尾→对头:队伍长度=(u人-u队)×时间
(8)典型行程模型:
等距离平均速度
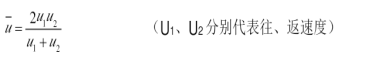
等发车前后过车
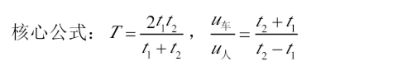
等间距同向反向
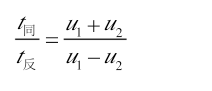
不间歇多次相遇
单岸型:
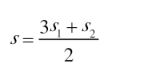
两岸型:
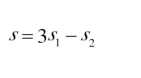
无动力顺水漂流 (其中t顺和t逆分别代表船顺流所需时间和逆流所需时间)
(其中t顺和t逆分别代表船顺流所需时间和逆流所需时间)
五、利润问题
(1)利润=销售价(卖出价)-成本;
利润率=利润/成本=销售价-成本/成本=销售价/成本-1
(2)销售价=成本×(1+利润率);成本=销售价/1+利润率
(3)利息=本金×利率×时期;本金=本利和÷(1+利率×时期).
本利和=本金+利息=本金×(1+利率×时期)=本金×(1+利率)ⁿn代表期限
月利率=年利率÷12; 月利率×12=年利率.
例:某人存款2400元,存期3年,月利率为10.2‰(即月利1分零2毫),三年到期后,本利和共是多少元?”
解:2400×(1+10.2%×36)=2400×1.3672=3281.28(元)
六、年龄问题
关键是年龄差不变:①几年后年龄=大小年龄差÷倍数差-小年龄
②几年前年龄=小年龄-大小年龄差÷倍数差
七、指数增长
如果有一个量,每个周期后变为原来的A倍,那么N个周期后就是最开始的Aⁿ倍,一个周期前应该是当时的1/A.
八、余数同余问题
核心口诀:“余同取余、和同加和、差同减差、公倍数做周期”
注意:n的取值范围为整数,既可以是负值,也可以取零值。








