政华教育

【例1】两超市分别用3000元购进草莓。甲超市将草莓按大小分类包装销售，其中大草莓400千克，以高于进价1倍的价格销售，剩下的小草莓以高于进价10%的价格销售。乙超市按甲超市大、小两种草莓售价的平均值定价直接销售。两超市将草莓全部售完，其中甲超市获利 2100 元(不计其他成本)，则乙超市获利多少元？（）

A.1950元 B.1800元 C.1650元 D.1500元

【答案】C。【解析】：设草莓的进价为x元/千克，则甲、乙超市均进草莓(3000÷x)千克，根据题意可知，甲超市大草莓的售价为2x元/千克，小草莓的售价为1.1x元/千克，乙超市所有草莓的售价均为(2x+1.1x)÷2=1.55x 元/千克。则乙的盈利额为(1.55x-x)×(3000÷x)=0.55×3000=1650元，故答案选择C。

【例2】某件商品如果打九折销售，利润是原价销售时的2/3；如果打八折后再降价50元销售，利润是原价销售时的1/4。该商品如果打八八折销售，利润是多少元？

A.240 B.300 C.360 D.480

【答案】C。【解析】：设商品原价为x元，进价为y元，根据题干可得方程组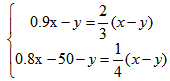，解得x=2000 ，y=1400 ，所以打八八折时，利润为0.88×2000-1400=360 元。故答案选择C。

【例3】某蔬菜商店购进一批西红柿，按 30%的利润率定价，卖出 70%后，为了尽快销售完，剩下的全部按照定价的半价出售。销售完后，商店获得的利润率是多少？（）

A.10% B.10.5% C.16.5% D.21%

【答案】B。【解析】：设西红柿的单位成本为x，购进数量为 y，则定价为1.3x，卖出了70%后，获利0.3x×0.7y=0.21xy，剩余30%的西红柿，售价为1.3x÷2=0.65x，获利(0.65x-x)×0.3y=-0.105xy，故总共获利 0.21xy-0.105xy=0.105xy，总成本为 xy，故商店获得的利润率为 0.105xy÷xy×100%=10.5%。故答案选择B。

从以上的例题分析中可以看出，利润问题并不难，核心是要在掌握公式的基础上，分析清楚题目中的等量关系，如果题目中已知的量比较多时，也可以通过列表展示出已知量，便于求解。

行测数量关系抽屉原理解题技巧

在行测试卷中数量关系对于很多小伙伴来说，一直是“老大难”问题。因其所需时间较长、难度较大，所以一般不是我们第一时间选择做的题目，不过其中有一部分题目我们是可以通过前期方法的积累，在做题时通过较短的时间便解出答案，今天就带着大家一起学习的抽屉原理，那么下面一起来看一下如何解决这类问题。

抽屉原理初定义

若把多于n件物品放入n个抽屉中，则一定有一个抽屉的物体数不少于2件，若有多于m×n个物品放入n个抽屉中，则一定有一个抽屉中的物品书不少于m+1件。

抽屉原理的核心

均、等、接近的思想，相信大家在看完后大多一头雾水，所以我们还需要通过其模型来帮助我们进行理解。

模型：假如我们现在有3个苹果放到2个抽屉里，那么至少有一个抽屉里的苹果数大于等于两个。

解析：因为如果我们哪怕每个抽屉里都放一个，那么还剩下一个必须放入其中一个抽屉中，所以至少有一个抽屉里有2个苹果。那么这就是抽屉原理的核心含义所在，也就是均、等、接近的思想。

抽屉问题

其定义为：给定若干个苹果数和若干个抽屉数，在某种要求下怎么放置苹果，能达到最大或者最小的情况，问这种情况是什么，这就是抽屉问题。

而我们需要注意到，抽屉问题都是由五大元素构成：苹果数、抽屉数、要求、方法和结果。在这里“苹果数”就是问题中较多的一方，“抽屉数”便为较少的一方，“放法”就是在具体的“要求”下，为达到某种“结果”的唯一放置状态。那么接下来我们通过几道例题来帮助我们加深一下理解。

典型例题

【例题】若干本书，发给50名同学问：

(1)每名同学都能拿到书，至少需要多少本书就有可能有同学拿到四本？

(2)无论怎么发，至少需要多少本书才能保证有同学拿到四本？

【解析】：第一问中书的数目就是我们所说的“苹果数”，而同学数(50名)就是其中的“抽屉数”，“要求”为每名同学都能拿到4本，想要达到的“结果”为可能有同学拿到4本。因为只要有可能，所以对应的“放法”就是首先符合要求的让50名同学先各得到1本，此时再令其中任意一名同学再得到3本，那么就能有一个同学有4本书。所以本题至少需要50+3=53本书。

第二问中其“要求”变为无论怎么放，想要的“结果”中多了保证二字，所以我们在考虑放法时便需要考虑其最坏的情况，也就是每名同学都先分到3本书，这样已有50×3=150本书，此时再有一本书分给任意一名同学都能达到我们想要的结果，即为50×3+1=151本。

通过刚才的比较，我们可以发现在解题过程中要区分好“至少可能”与“至少才能保证”，这样我们就可以按照刚才的思路去尝试解决问题啦。以上就是抽屉原理的解题小技巧，大家学会了吗？

行测技巧：行程问题莫慌张，数形结合来帮忙

在行测考试的数量关系部分中，行程问题是考查频率非常高的题型之一，很多考生遇到这类题目时比较头疼，不知道从何处入手。其实，大部分行程类题目只要我们能够一边读题，一边清晰直观地画好行程图，从行程图中线段与线段之间的关系，就可以快速找到等量关系列出方程。采用数形结合的方式，便可以将行程问题化繁为简，清晰直观地找到答案，下面通过几道题目来感受一下：

【例1】一辆客车与一辆货车从东、西两个车站同时出发匀速相向而行，客车和货车的行驶速度之比为4∶3。两车相遇后，客车的行驶速度减少10%，货车的行驶速度增加20%，当客车到达西车站时，货车距离东车站还有17公里。东、西两个车站的距离是( )公里。

A.59.5 B.77 C.119 D.154

【答案】C。【解析】根据题意，设客车速度为4v公里/小时，货车速度3v公里/小时，则相遇后客车的速度为3.6v公里/小时，货车的速度为3.6v公里/小时。设客车和货车经过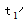小时相遇，相遇后客车经过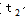小时到达西车站，结合题意画出行程图，根据图中线段间关系可得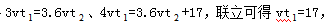，则东、西两个站的距离为公里，故答案选择C。

【例2】甲公司的马经理从本公司坐车去乙公司洽谈，以30千米/时的速度出发20分钟后，马经理发现文件忘带了，便让司机以原来1.5倍的速度回甲公司拿，而他自己则以5千米/时的速度步行去乙公司。结果司机和马经理同时到达乙公司。甲乙两公司的距离是( )千米。

A.12.5 B.13 C.13.5 D.14

【答案】A。【解析】由题可知，马经理行驶了30×20/60=10千米发现文件忘带，设马经理步行再用t小时到达乙公司，根据提议画出行程图，观察图中线段之间的关系可得10+5t=30×1.5t-10，解得t=0.5，则甲乙两公司的距离是10+5×0.5=12.5千米，故答案选择A。

行测数量关系：方程法解环形相遇追及问题

很多考生在备考各类行测考试时，都会对数量关系比较头疼，感觉没有时间去完成数量关系的题目，所以在考试的时候学会挑题很关键。而在数量关系当中有一些题目一般情况下通过方程法都是可以解决的。就比如说行程问题中有些题目，题干设定通常是有人绕着公园或者田径场运动，运动的路径能够形成闭环，我们把这类问题称之为环形相遇追及问题，这些就是可以通过方程法来解决的。

环形相遇

环形相遇是指两个人在环形跑道上反向而行，一个人顺时针运动，另一个人逆时针运动，出发之后，经过一段时间在环形跑道上某一点两个人相遇。如果两个人是同时同地出发，则第一次相遇时，两人运动的路程之和等于环形跑道的周长，第n次相遇时，两人所走过的路程之和等于n倍的跑道周长。

【例1】小王和小张两个人在周长为1200米的公园散步。小王每分钟走65米，小张每分钟走55米。现在两个人同时从同一地点反方向行走，那么出发后多少分钟他们第二次相遇？（）

A.10 B.20 C.30 D.40

【答案】B。【解析】：小王和小张两人同时从同一地点反方向行走，第二次相遇时，他们所走过的总路程为公园周长的两倍，即1200×2=2400米，则所花费的时间为2400÷(65+55)=20分钟，故选择B选项。

环形追及

环形追及是指两个人在环形跑道上同向而行，两人都顺时针或者都逆时针运动，出发之后，经过一段时间速度较快的人追上速度较慢的人。如果两个人是同时同地出发，则第一次追上时，两个人的路程之差等于跑道的周长，第n次追上时，两个人的路程之差等于n倍的跑道周长。

【例2】小王和小张两个人在周长为1200米的公园跑步。小王每分钟跑120米，小张每分钟跑90米。现在两个人同时从同一地点同方向行走，那么出发后多少小时他们第三次相遇？（）

A.60 B.80 C.100 D.120

【答案】D。【解析】小王和小张两人同时从同一地点同向行走，当小王第三次追上小张时，小王与小张走过的路程差应该为3倍的公园周长，即3×1200=3600米，则所花费的时间为3600÷(120-90)=120分钟，故选择D选项。

应用

【例3】小王和小张两人在一条400米的运动场上在同一地点同时出发同向匀速跑步。当小王第二次追上小张的时候，小张跑了1200米。问小王的速度是小张的多少倍？（）

A.1.2 B.1.5 C.1.6 D.2.0

【答案】D。【解析】：根据环形跑道周长为400米两个人在同一地点同时出发同向匀速跑步可知，小王第一次追上小张时，比小张多跑一圈，即400米，同理小王第二次、第三次追上小张时，均比小张多跑一圈，即400米。相同时间内，小张跑了1200米，小王跑了1200+400×3=2400米，当时间一定时，路程与速度成正比，故小王、小张两人的速度比等于路程比，即2400∶1200=2。故选择D选项。

行测备考：锤炼审题能力，解决复杂计算

在每年行测考试中，数学应用题总是让诸位考生望而却步，为难考生的不光是应用题涉及的知识点，还有复杂的数量关系，以及隐藏在内部的逻辑关系，但是从近两年的考试来看，考试覆盖的知识面变窄，15道题所涉及的知识点不超过10个，但题目变得综合，一道题目可能涉及多个知识点，这就需要考生去锤炼审题能力，遵从题目本身，一步一步地题目梳理清楚，从而解决这一类问题。

【例1】社区工作人员小张连续4天为独居老人采买生活必需品，已知前三天共采买65次，其中第二天采买次数比第一天多50%，第三天采买的次数比前两天采买次数的和少15次，第四天采买次数比第一天的2倍少5次。问：这4天中，小张为独居老人采买次数最多和最少的日子，单日采买次数相差多少次？（）

A.9 B.10 C.11 D.12

【答案】C。【解析】本题是一道计算问题。题目的基本特点是所涉及的数量较多，需要对题干进行仔细地梳理。首先，第一句话“小张连续四天采买生活必需品”；明确“四天”这个条件即可；其次，“前三天共采买65次”，这里提到了前三天的采买次数，可以设这三天的采买次数分别为x，y，z，可列式：x+y+z=65；再次，“第二天采买次数比第一天多50%”，这里就可以列出一个式子。y=x×(1+50%)=1.5x；第四，“第三天采买的次数比前两天的和少15次”，可列式：z=(x+y)-15=2.5x-15。综上，可列式：x+1.5x+2.5x-15=65，解得x=16；第五，“第四天采买次数比第一天的2倍少5次”，可以用第一天表示第四天，即2x-5；最后问题问的是为老人采买次数最多的日子和最少的日子，采买次数相差多少？由x=16，可以知道四天的次数分别是16、24、25、27，所以所求是27-16=11次，答案选C。

【点拨】本题题干较长，但是依照上述梳理下来，还是很清楚的。所以遵从题目本身去梳理题干，在梳理的过程中，最终的问题就从未知到已知了。

【例2】某企业参与兴办了甲、乙、丙、丁4个扶贫车间，共投资450万元。甲车间的投资额是其他三个车间投资额之和的一半，乙车间的投资额比丙车间高25%，丁车间的投资额比乙、丙两车间投资额之和低60万元。企业后期向4个车间追加了200万元投资，每个车间的追加投资额都不超过其余任一车间追加投资额的2倍。问：总投资额最高和最低的车间，总投资额最多可能相差多少万元？（）

A.70 B.90 C.110 D.130

【答案】C。【解析】本题与上题的描述比较类似，也是遵从题目本身去审题。首先，“某企业参与兴办了4个扶贫车间，共投资450万元”，即甲+乙+丙+丁=450万元，其次；“甲车间投资额是其他三个车间投资额之和的一半”，即甲=1/2×(乙+丙+丁)，由以上两个式子可知甲=150，乙+丙+丁=300万元；再次，“乙车间的投资额比丙车间高25%”，即：乙=丙×(1+25%)=1.25丙，第四，“丁车间比乙、丙两车间投资额之和低60万元”，即：丁=(乙+丙)-60=2.25丙-60，由以上可知1.25丙+丙+2.25丙-60=300，解得丙=80，所以乙=100，丁=120；第五，“每个车间的追加投资额都不超过其余任一车间追加投资额的2倍”，也就是说，往任一车间追加的投资额最多也不能超过其余三个车间中投资额最少的车间的2倍；第六，问题问的是总投资额最高和最低的车间，总投资额最多可能相差多少万元？也就是说问的投资额最高和最低的车间所相差的最大值，换句话说就是最高的尽可能高，最低的尽可能低。由上述可知追加之前甲最多，丙最少，假设甲追加X元，丙最少也要追加1/2x，所求就是(150+x)-(80+1/2x)=70+1/2x，而总追加额为200万，又满足甲尽可能多，那乙、丙、丁的追加金额只能是一样的1/2x，所以x+3/2x=200，x等于80，所以70+1/2×80=110万元。故选择C选项。

综上，两道题都是考试题，题目中的条件比较多，但是如果慢慢的一步一步地去审题，还是能够将题目梳理的清楚明白，每年考试这类题目较多，如果想要拿分，同学们还是要多花时间去训练。