政华教育

在行测考试中朴素逻辑的考题是广大考生都有畏难情绪的题型，一般这类题目对我们的综合推理能力要求比较高。其实朴素逻辑有很多考题都有固定的考查类型，其中一类就是依据题干中每个人只说对一半来解题，这类半真半假题目往往题干信息较多，看起来相对凌乱，很多考生第一反应会觉得束手无策。其实只要找准突破口，这类题目就能迎刃而解了。下面就带着大家了解，如何利用关联性信息作为突破口，顺藤摸瓜解半真半假题。

【什么是关联性信息】

关联性信息一般表现与其他信息相关性强，或者反复出现的高频信息。在解决半真半假的题型中，首先关注这类信息，能够更快速找到有效条件，进而顺藤摸瓜推理出正确结论。

比如，题干告诉我们三个信息：①小张周一上课，小王周三上课；②小张周三上课，小李周一上课；③小张周二上课，小黄周一上课。问已知每个信息都只猜对了一半，小王上课的时间是？

这道题目中哪些信息存在关联性呢？

观察可知，第一句前半句谈到的小张和周一，在之后的几句话中反复出现，也就是说，第一句的前半句与后面的信息关联性比较强，所以可以考虑从第一句话的前半句出发，进行推理。

如果说第一个信息前半句为真，那么与之关联的第二个信息的前半句就一定为假，后半句也一定为假，与题干已知“猜对一半”的条件存在冲突。所以可以判断出第一个信息的前半句一定为假。据此可以进行推理，既然“猜对一半”，所以第一个信息的后半句一定为真，得出小王周三上课，本题得解。

【例题】幼儿园马老师和三个小朋友情情、可可和安安一起玩“猜一猜，我最棒”的游戏。马老师对小朋友们说：“我把手中的红球、黄球和蓝球分别放在这个柜子的三个抽屉里，请你们猜一猜每只抽屉里放的是什么颜色的球？猜对了奖励小红花！”然后，她请小朋友们闭上眼睛，把三只球分别放在三个抽屉里。小朋友猜的情况如下：

情情说：“红球在最上层的抽屉，黄球在中间抽屉。”

可可说：“红球在中间抽屉，蓝球在最上层的抽屉。”

安安说：“红球在最底层的抽屉，黄球在最上层的抽屉。”

老师告诉她们，每人都只猜对了一半。

问题：请问红球、黄球和蓝球各在哪一层抽屉里？（）

A.红球在中间抽屉，黄球在最上层的抽屉，蓝球在最底层的抽屉

B.红球在中间抽屉，黄球在最底层的抽屉，蓝球在最上层的抽屉

C.红球在最上层的抽屉，黄球在最底层的抽屉，蓝球在中间抽屉

D.红球在最底层的抽屉，黄球在中间抽屉，蓝球在最上层的抽屉

【答案】D【解析】观察题干发现，红球和最上层出现的频率最高，情情的前半句话中既有红球，又有最上层，与其他信息的关联性极强，所以从情情的前半句话出发，进行推理。

如果情情的前半句话是真话，那么可可的前半句和后半句都是假话，此时与“每人都猜对一半”的条件冲突，于是得出情情前半句话一定是假话，又因为“每个人都猜对一半”，所以情情后半句话一定是真话，也就说明黄球在中间层，故本题选D。

特殊模型之求异论证

判断推理在国省考中占有很大的比例，逻辑判断部分又是判断推理中一个重点难点。逻辑中占比最大的削弱加强题目是大家比较头疼的地方，其实在削弱加强题目中也存在一些固定的基本模型，这些模型有固有的削弱和加强方式，通过对特殊的模型的学习，我们在做题的时候可以快速准确地选出正确答案。接下来带大家一起来看一下其中的一个特殊模型，求异论证。

求异论证，研究的是两组实验对象中两个不同点之间的因果关系。如有两个实验大棚种有相同数量的黄瓜苗，其中一个施加镁盐，另一个不加，结果加入镁盐的产量比不加镁盐的产量高，于是就得出镁盐可以提高黄瓜产量。

求异论证常见的削弱和加强方式

削弱：1.切断因果联系。2.另有他因(找两组实验间的不同点)。3.因果倒置。

加强：1.建立因果联系。2.排除他因(找两组实验间的相同点)。

知道削弱加强方式之后，我们具体怎样运用呢？下面我们来结合题目来具体分析一下。

【例题】某调查发现，患抑郁症的人平均每天使用手机的时间在122分钟以上，而没有患抑郁症的人平均每天使用手机的时间为59分钟。有人提出，玩手机可能会影响情绪，使用手机的时间越多，抑郁的可能性越大。

以下哪项如果为真，不能支持以上结论？（）

A.长时间玩手机，尤其是睡前玩手机，可能会造成睡眠时间的不足，而导致情绪容易出问题

B.长时间玩手机，会接触海量数据，这些数据不能及时处理，易造成情绪低迷、烦躁和疲劳，增加抑郁风险

C.人把过多时间和精力放在手机上，必然和现实中的人接触减少，逃避面对现实是抑郁的特征之一

D.长期玩手机的人，通常把大部分时间用在上网和打游戏，而不是和朋友聊天，缺少人际支持是抑郁的风险因素

【答案】C【解析】首先分析题干，题干通过一项调查发现，抑郁症患者的平均玩手机时间比没有患抑郁症患者的平均时间多，于是就得出结论：使用手机的时间越多，抑郁的可能性越大。属于典型的求异论证模型，那我们分析一下选项，哪一个不能支持。

A项长时间玩手机会造成睡眠不足进而导致情绪问题，也就意味着长时间玩手机确实可能增加抑郁风险，能够支持。

B项长时间玩手机会增加抑郁的风险，建立了不同点之间的因果联系起到了支持的作用。

D项长时间玩手机导致缺少人际支持从而增加抑郁风险，也起到了支持的作用。

C项说的是抑郁的特征，而不是玩手机时间和抑郁的关系，不能支持。综上A、B、D都从不同角度对结论起到了支持的作用，故本题选C。

可能性推理易错怎么办

可能性推理是行测判断推理这一部分中的常考题型，也是容易出错的一类题型，突破这类题对提高行测分数有很大帮助。而可能性推理中常考的一类题型就是因果分析。为了帮助考生突破这类题目，在此就因果分析中的一种情况进行具体说明。

这类题目特点就是：题干讨论因果关系，比如讨论A是否可以导致B，选项却只是说A和B同时存在。下面通过例题进行详细讲解。

【例题】公元250年至800年，玛雅文明还十分发达。城市繁荣，庄稼收成也很喜人。气候记录显示，这一时期玛雅地区的降水量相对较高。此后玛雅文明开始衰落。从公元820年左右起，在连续95年的时间里，该地区开始经历断断续续的干旱，有些地方的干旱甚至持续了数十年之久。许多专家由此认为，9世纪的气候变化或许正是玛雅文明消亡的原因。

以下哪项如果为真，最能支持上述专家的观点？（）

A.在9世纪衰退的玛雅城市大多分布在南部，使用木材进行的建造活动也大大减少

B.和所有大型农耕文明一样，玛雅人的社会很大程度上依赖于农作物，干旱导致农产品减少，严重影响玛雅人的生存

C.大多数玛雅城市是在公元850年到925年之间衰落的，和干旱发生的时间高度重合

D.公元1000年至1075年期间，玛雅地区石雕和其他建造活动减少了将近一半，而那时当地又一次遭受了严重的旱灾

【答案】B【解析】题干中专家得出一个观点：9世纪干旱气候变化或许是玛雅文明消亡的原因。

A项告诉我们玛雅城市建造活动减少了，说明确实可能存在文明消亡的迹象，但是题干讨论的是玛雅文明消亡的原因是什么？A项只说了可能存在消亡的迹象，但消亡的原因到底是什么呢？A项并没有说，所以不能支持，排除。

B项给我们解释了干旱气候是如何导致玛雅文明消亡的，就是因为干旱会导致农产品减少，农产品减少会影响玛雅人的生存，所以气候变化可能是玛雅文明消亡的原因，支持了题干的观点，保留。

C项说的是玛雅城市衰落的时间和干旱的时间重合，但是题干讨论的是玛雅文明消亡的原因是什么？虽然干旱和衰落的时间重合，但是干旱和衰落之间是否具有因果关系呢？选项没有说清楚，那也就不能确定气候变化是否是玛雅文明消亡的原因，不能很好地支持，排除。

D项告诉我们11世纪玛雅地区遭遇了旱灾。但是题干讨论的是9世纪玛雅文明消亡的原因。11世纪的情况并不能说明9世纪的情况，不能支持，排除。故本题选B。

此题中题干认为9世纪干旱气候变化或许是玛雅文明消亡的原因，也就是A(9世纪干旱气候变化)导致了B(玛雅文明消亡)。

选项C说A(9世纪干旱气候变化)和B(玛雅文明消亡)同时存在，同时存在未必具有因果关系，不能起到很好的支持作用，所以排除该选项。

图形推理：“圆”来是你

判断推理中的图形推理，因为考点多、变化多、题量大，一直是很多同学头痛的部分，在国考和湖南省的考题当中，虽可能有特殊题型和新考点，但整体图形推理的规律考查较为常规，我们需要通过做大量的试题，熟悉高频考点，提高图形敏感性，这样才能在拿到题目的时候有一个思考范围，考场上就能节省时间，尽量多的做对题目。那么接下来给大家分享一个高频考点——特别的“圆”。

在公务员考试中圆经常出现，而且考点变化多。今天给同学们整理一下圆的一些常见的考点和变化规律，方便后续遇到了问题能够快速的识别规律，做出题目。

【例题1】从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。（）

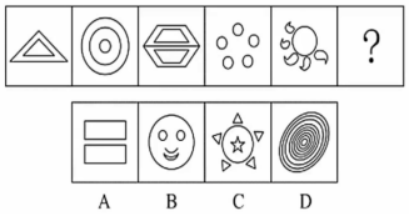
【答案】C【解析】观察题干发现是顺推型题干，依次观察题干给出的五个图形，好几个图形都有圆出现。那么圆，而且每个图形内部都是完成的封闭。我们可以首先考虑一下封闭区域数量。题干封闭区域数量依次是2、3、4、5、6所以我们应该选择一个七个封闭区域的，故本题选C。所以圆出现我们可以考虑封闭区域数量。

【例题2】从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。

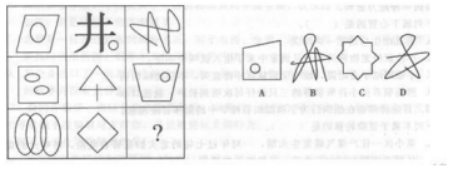
【答案】A【解析】题目考查交点数，题干交点数都为4，选项交点数为4的只有A。故本题选A。

【例题3】从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。（）

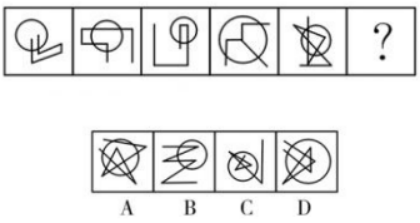
【答案】C【解析】观察题干会发现每个图形都有圆出现，那么这里我们可以考虑一下圆内圆外两个世界，圆内的交点数，圆内部的交点数依次是0、1、2、3、4，所以选一个圆内部五个交点的，故本题选C。那么此题考的是元内部的交点数，偶尔也会考圆内部的封闭区域数、部分数、笔画数等等。