
行测图形推理小众考点总结
行测图形推理:把握“小众”考点
图形推理是行测考试中的必考题。但是各位考生在做图形推理的时候往往会面临这样一个问题:一些题目思考了很多考点,花费了大量时间,仍然没有找到合适的规律。此时题目可能考查的是不太容易想到,今天政华教育给大家总结一下这些“小众”考点。
考点1:一笔画(一笔画成图形)
知识点
一笔画要满足三个条件:①笔不离纸。②线不重复。③走遍所有路径。
什么样的图形能够一笔画?奇点数为0或2个的图形能一笔画。
什么是奇点?由一个点发射出奇数条线,这个点为奇点。
例题
例1:判断下图中的点是否为奇点
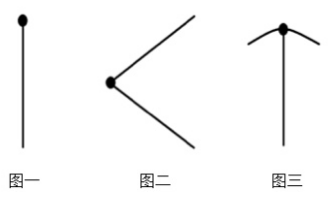
图一发射出1条线,故为奇点。
图二发射出2条线,不是奇点。
图三发射出3条线,故为奇点。
注:线条不分直线曲线,端点也是奇点。
例2:判断下图能否一笔画

图四有2个奇点,故能一笔画。
图五有4个奇点,不能一笔画。
注:多笔画的笔画数=奇点数/2。
例3:把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:( )
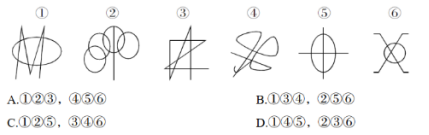
【答案】A【解析】观察图形相似度比较低,观察其他考点没有合适的规律,且图形端点比较多,那此时可以考虑一笔画。图形①有两个奇点,能够一笔画。图形2两个奇点,能够一笔画,图形③两个奇点,能够一笔画。所以图形①②③一组。剩下的图形④⑤⑥都有四个奇点,都是两笔画。故本题选A。
通过上面例题,相信各位考生对一笔画这一考点有了一定的了解,在日常做题中,如遇到图形相异,且端点较多时,一定要想到一笔画这一考点。
考点2:全部求同
知识点
全部求同是指一组图形中都包含同一种元素。
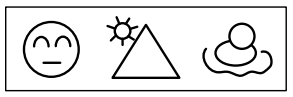
如上图中三个图形都含有圆。
例题
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规性:( )
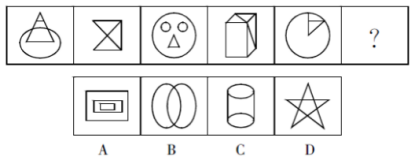
【答案】D【解析】观察上述图形,都有相同的构成元素“三角形”。故本题选D。
通过这道例题,各位考生会发现,全部求同这样简单的考点却更容易被忽略,所以同学们需要多巩固训练,也要加强对小众考点的练习。
以上就是今天给大家介绍的知识点,“小众”知识点本身并不难理解,关键在于考试时要考虑到存在这样的考点,也希望各位考生在实际做题中多积累一些“小众”知识点,灵活运用。
行测图形推理“点起来”
图形推理,是各位小伙伴们在备考行测时需要重点关注的一个部分。然而很多小伙伴在做图形推理题目时,仅凭感觉和运气,毫无章法,往往琢磨许久也分析不出图形中隐藏的规律。那么,如何才能掌握这类题型呢?观察历年试题,稍加研究便能发现,很多题目虽然出题形式和所画图形千差万别,但所考考点却大同小异。正所谓万变不离其宗,变化的是形式,不变的是考点,掌握这些不变的考点才是我们备考的重点。在历年考试题目中,图形推理中点的数量既是考试的重“点”,也是难“点”。今天,政华教育跟大家来聊一聊图形中的“点”。
点的总数
在数图形的点数时,主要有两种考法:一是点的总数,二是某种点的个数。前者相对后者而言,难度较低,且在近几年考试中,出题频率有所下降。我们通过一道题目来观察一下。
例1:从下列所给的四个选项中,选择最合适的一个填入问号内,使之呈现一定的规律性:( )
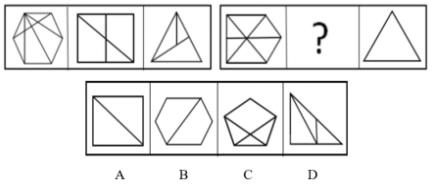
【答案】D【解析】图形组成元素不同,优先考虑数量关系类规律。图形中交点特征比较明显,优先考虑数交点。
第一组图形中,三个图形的交点数分别为9、7、5;第二组中图形交点数分别为7、?、3,所以问号处的图形交点个数应为5,只有D项符合。因此,选择D选项。
某种点数
除了数所有交点数以外,单独数某种点数也是常见的考点。根据图形特点,点的分类主要有以下三种:
1.图形有相切
当图形中出现线条相切的情况时,优先考虑数切点或交点。注意,切点是一种特殊的交点,若图形考察交点个数,那么切点也应该包括在内。
例2:把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:( )
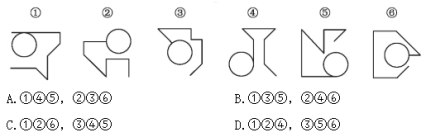
【答案】A【解析】图形组成元素不同,优先考虑数量关系类规律。图形中出现线条相切的情况,考虑数切点。
①④⑤中圆和直线相切,均有1个切点,②③⑥中圆和直线相交,均有1个交点,无切点,据此分为两组。因此,选择A选项。
2.图形有曲线
当图形线条中有曲线时,可以考虑曲线与直线的交点、曲线与曲线的交点。其中,考察曲直交点的题目较多。
例3:从所给的四个选项中,选择最合适的一个,使之呈现一定的规律性:( )
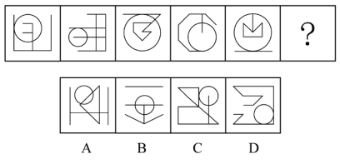
【答案】C【解析】图形中出现线条相切的情况,数点特征明显,考虑数点。出现曲线线条,所以优先数曲直交点。
所给图形均有两个曲直交点,排除B选项,对比剩余选项,区别在于切点个数。已知图形中,两个曲直交点分别为一个交点一个切点,只有C项符合。
注意:本题若只数切点个数,则图形中切点个数均为1,仍可选出C选项。因此,选择C选项。
3.图形有内外
当图形数点特征明显,且图形可分为内外两部分时,我们主要考虑三种点:图形内部点(封闭区域内部的点)、图形内外交点(外框与内部线条交点)及外框上的点。
例4:从所给的四个选项中,选择最合适的一个,使之呈现一定的规律性:( )
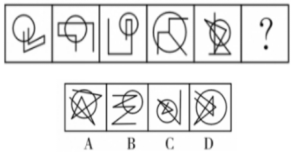
【答案】C【解析】图形组成元素不同,优先考虑数量关系。图形中交点较多,考虑数点。图形中圆可当作曲线,也可当作封闭区域来看,当作曲线时,图形曲直交点个数规律不成立,所以考虑分内外观察图形。
已知图形中圆形内部交点数量分别为0、1、2、3、4,所以问号处圆内部交点数为5。因此,选择C选项。
以上就是图推中点的常见规律,希望大家熟知并掌握。政华教育建议大家可以搜集一些相关图推题目进行大量练习,在做题中消化吸收,做到事半功倍。
行测图形推理:走进立体图形之六面体外表面展开图
在行测考试中,六面体展开图一直是考查的重难点,尽管看起来比较简单,但对立体空间感不强的考生来说还是比较难的,接下来政华教育为大家介绍常用四种做题思路。
对立面排除法
在立体图形中相对面是不相邻的,所以如果在选项的立体图中同时出现两个相邻的相对面可以直接排除。(判断对立面:在展开图中相隔一行/列且与相隔的行/列有公共边的两个面即为对立面)
例1
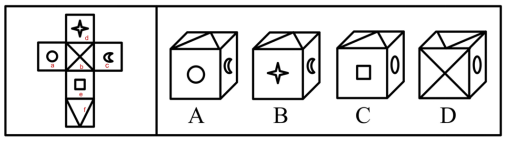
【答案】C【解析】在展开图中面1与面3相隔列2,故为对立面,A选项中存在对立面相邻,故可排除;面2与面5相隔列3,故为对立面,B选项中存在对立面,故可排除;面4与面6相隔行2,故为对立面,D选项中存在对立面,故可排除,故本题答案选C。
非对称中心图形定位法
在选项中选取一个非对称图形的面或者非重复的面作为参考面,观察选项中参考面的相邻面是否与展开图一致。
例2
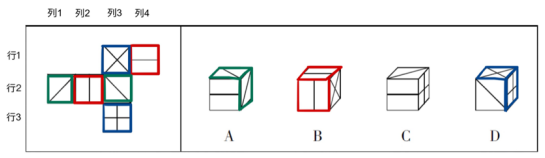
【答案】C【解析】先看A选项,面a与面c为对立面,相邻,排除。B选项以c面作为参考面,那么B项中的正面应该为展开图中的面b,与B选项不一致,排除。D选项面b和面f为对立面,相邻,排除,故本题答案选C。
画边法
首先,结合选项,确定一个特殊面(非重复面和非中心对称面),然后,确定面中的起点,按照顺时针方向画边,最后选项和展开图匹配,不一致则排除。
例3
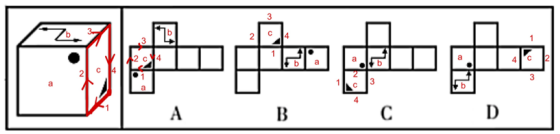
【答案】C【解析】首先以面c作为参考面,以c面中黑色三角形的直角点为起点,顺时针一次标注1-4,如果所示,边2与面a相接,边3与面b相接,观察A选项,a、c两面相接于边1与展开图不一致,排除。观察B选项,b、c两面相接于边4,与展开图不一致,排除。观察D选项,b、c两面相接于边3,与展开图不一致,排除。故本题答案选C。
以上三种方法需要结合具体的展开图特征选用合适的方式实现快速解题,需要广大考生熟悉解题方法的应用,多做练习以达到学以致用。
行测对称图形当真如此简单吗?揭露对称性“心机”考点
对称性图形是行测图形推理题目中常客。这种图形也因其形式简单让考生青睐,成为考生喜欢的题目类型之一。但是,正是这种大家认为简单的题目,我们也未必都能正确判定。所以,大家可千万不能被这类图形表面的单纯形象所蒙骗,还是需要明确对称性的知识点,尤其是对它的一些“心机”考点做到心中有数。
对称图形常见考点
1.对称性的判定。
对称图形可分为轴对称、中心对称、既是轴对称又是中心对称图形。
例题:把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是( )。
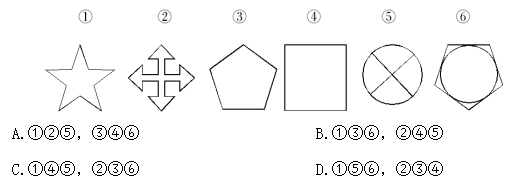
A.①②⑤,③④⑥ B.①③⑥,②④⑤
C.①④⑤,②③⑥ D.①⑤⑥,②③④
【答案】B【解析】图形①③⑥都是竖直对称图形;图形②④⑤都是中心对称图形。
2.轴对称图形轴的数量及方向。
例题:从所给的四个选项中,选出一个填入问号处,使之呈现一定的规律性。( )
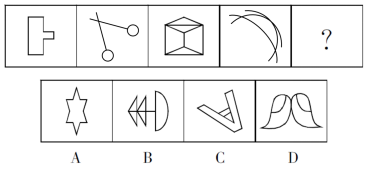
【答案】B【解析】每个图形都只有一条对称轴,且对称轴方向顺时针旋转45°,答案选B。
对称图形“心机”考点
1.对称图形有其他特征。
例题:从所给的四个选项中,选出一个填入问号处,使之呈现一定的规律性。( )
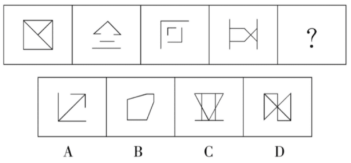
【答案】B【解析】题干图形均对称,对称轴的方向依次逆时针旋转45°,因此排除C、D。再次观察图形发现,图形均有线条构成,线条数均为6,排除A,满足条件的是B。
2.对称图形轴与原图位置关系。
例题:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。( )
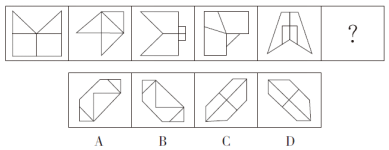
【答案】B【解析】题干图形均为轴对称图形,且对称轴方向依次顺时针旋转45°,因此问号处的图形应具有向右倾斜45°的对称轴,排除A、C。再次观察图形发现,奇数项图形中对称轴与图形的某一线段重合,偶数项图形中对称轴不与图形中的任一线段重合。问号处为第六个图形,应选择对称轴不与图形中任一线段重合的图形,排除D。故本题选B。
3.对称轴与对称轴位置关系。
例题:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。( )
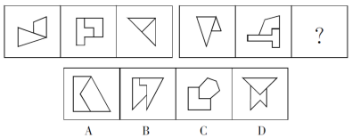
【答案】D【解析】题干第一组图形整体并不都是对称性图形,但图形均由两个对称小图形组成,分别找出小图形的对称轴。发现第一个图形中两个小图形的对称轴是平行分布的,第二个图形中两个小图形的对称轴成45°夹角,第三个图形中两个小图形的对称轴成90°夹角。类比到第二组图形中规律依然满足,因此问号处需满足两个小图形的对称轴成90°夹角,答案选择D项。
政华教育相信大家通过上述题目及其所对应的规律,能够对对称图形的知识点有进一步的了解,既要掌握简单题目,也要了解“心机”考点。最后,政华教育建议大家对此类题目多多练习,真正做到熟练运用。








