政华教育

我们从小学开始接触加减运算，当时学校里面讲到的加减运算是从后往前进行计算，例如：22875+52837+99865，如果我们列竖式计算的话，我们应该依次计算个位、十位、百位、千位和万位，选择从个位开始加和的原因是有可能会有进位或借位，从后往前计算会在计算这一位数的时候考虑到下一数位的进位或借位问题，但是当选项不适合用尾数开始计算时，我们可以从高位开始计算，兼顾到下一数位的进位和借位问题即可。

例题：25621+37124+72563=( )。

A.不到11万 B.11万~12万之间

C.12万~13万之间 D.超过13万

【答案】D【解析】对于这种题目如果用尾数法的话，我们得计算到倒数第5位之后才能判断究竟应该在哪个范围，基本上就相当于精算了。那应该怎么计算呢？观察选项我们会发现选项之间的区别在于万位这四个是各不相同的A选项是不到11万，B是11万多，C是12万多，D是超过13万，那也就说明其实我们只要知道最终结果的万位数是几就可以了，那如果要想知道万位可以直接取原式三个数中万位及以上数位上的数进行计算，即计算2+3+7=12万，但是从首位开始计算时需要考虑下一数位的进位问题，也就是说万位上的数=万位加和+千位进位，此题千位加和为5+7+2=14，向万位进1，那么万位上的数就应该是12+1=13万，故本题应该选择D。

【小结】加法运算快速计算首几位有效数字时，根据选项判断需要精确计算的数位，将原式中该数位及以上数位上的数进行求和后加上下一数位的进位即可。

练习题：2015年-2018年A省人力资源专业毕业生人数分别为12921人、18982人、23654人、47191人。

问：2015年-2018年，A省人力资源专业毕业生总数为( )。

A.8万~9万 B.9万~10万

C.10万~11万 D.11万~12万

【答案】C【解析】问题所求为2015年-2018年毕业生总和，列式为12921+18982+23654+47191。根据选项可知，只要确定最终加和的万位数即可，依据上面讲过的方法，万位加和+千位进位=最终结果的万位数。万位加和为1+1+2+4=8万，千位进位为2+8+3+7=20进2，故最终结果的万位数应该为8+2=10万，选择C选项。

通过以上题目的训练，希望大家能够了解对于加法运算当选项中给出的是范围区间的话，快速确定首几位有效数字会更容易得出结果。

行测资料分析速算技巧之特征数字法

在行测资料分析的学习过程中，计算方法的学习是非常关键的。掌握高效的计算技巧可以达到事半功倍的效果，在资料分析的计算中掌握特征数字法就很好的说明这一点，政华公考在此给大家介绍一下这种计算方法。

一、什么是特征数字法

特征数字法就是利用百分数和分数之间的相互转化，将列式中的百分数近似地转化成一些特定的分数，从而达到简化计算的一种方法。

二、常见百分数与分数之间的转化

三、应用环境

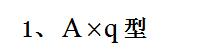
【例1】2017年上半年，小微服务业样本企业资产总计462.2亿元，2018年比2017增长25.9%。

问题：2018年小微服务业样本企业资产总计比2017年增长了( )亿元？

A.108.2 B.119.7 C.123.5 D.130.6

【答案】【解析】根据材料可知，2017年上半年，小微服务业样本企业资产总计462.2亿元，2018年比2017增长25.9%。所求为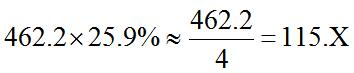，结果偏小选稍大的选项，本题选择B项。

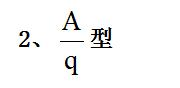
【例2】2018年，我国可再生能源发电量达1.87万亿千瓦时，同比增长约1700亿千瓦时；可再生能源发电量占全年发电总量比重为26.7%，同比上升0.2个百分点。

问题：2018年，我国发电总量约为( )万亿千瓦时。

A.1.87 B.3.70 C.5.84 D.7.00

【答案】D【解析】根据文字材料可知，2018年，我国可再生能源发电量为1.87万亿千瓦时，占全年发电量比重为26.7%，则所求为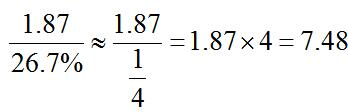亿千瓦时，结果偏大选稍小的选项，本题选择D项。

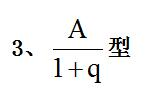
【例3】海州市海洋化工开发区，2012年完成总产值为147.5亿元，同比增长30.7%。

问题：2011年海州市海洋化工开发区的总产值是( )。

A.122.9亿元 B.112.9亿元 C.108.7亿元 D.106.6亿元

【答案】B【解析】

【例4】2007年全年地方财政支出1083.57亿元，比上年增长33.4%。

问题：2007年全年地方财政支出比上年增加了( )亿元。

A.269.58 B.271.30 C.362.55 D.360.44

【解析】B。由材料可知，2007年全年地方财政支出比上年增加了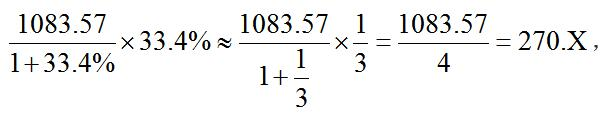结果偏小选稍大选项，本题选择B项。

四、总结

对于特征数字法，重点在于熟悉其常见的应用环境以及掌握百分数转换成分数的运用。同时，希望同学们继续关注“政华公考”，下载“政华公考”app，学习更多的做题技巧。

行测资料分析：“藏”在两数之比变化中的增长率

在行测资料分析中，可以写成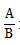形式的列式我们统称为两数之比，常考的有比重、平均数以及倍数，还有收入利润率、产销率等等。当我们已知分子分母的增长率的大小关系时，就可以直接判断现期两数之比与基期两数之比相比较的变化情况。

例题：2018年全年粮食种植面积11704万公顷，比上年减少95万公顷，减少0.8%。全年粮食产量65789万吨，比上年减少371万吨，减产0.6%。

问题：2018年全年粮食平均产量与上年相比提高了。(判断正误)

【答案】正确【解析】结合材料，问题所涉及的粮食产量看作A，粮食面积看作B，所以判断两数之比的变化，从材料中可知qa=-0.6%，qb=-0.8%，即qa>qb，现期比基期增加，所以2018年全年粮食平均产量与上年相比提高，故正确。

以上例题是该考点的基础考查形式，但其变形考查形式，成为了考生的复习痛点，不仅错误率居高不下，且常常会浪费掉大量时间。

接下来，一起看看“藏”在两数之比变化中的增长率。

例1：2018年末全国大陆总人口139538万人，比上年末增加530万人，其中城镇常住人口83137万人，占总人口比重(常住人口城镇化率)为59.58%，比上年末提高1.06个百分点。

问题：2018年末城镇常住人口增长速度比全国大陆总人口增长速度快。(判断正误)

【答案】正确【解析】所求为判断城镇常住人口增长速度和全国大陆总人口增长速度的大小关系，即两个增长率比较大小，结合材料，两个增长率并没有直接给出，但材料中给出城镇常住人口占全国大陆总人口的比重，以及比上年末提高1.06个百分点，即现期与基期比，比重上升，所以可以得到qa>qb，该比重中的A为城镇常住人口，B为全国大陆总人口，所以城镇常住人口增长速度大于全国大陆总人口增长速度，故正确。

例2：2018年全年总用水量6110亿立方米，比上年增长1.1%。人均用水量439立方米，比上年增长0.6%。

问题：2018年全年我国人口增长速度低于1.1%。(判断正误)

【答案】正确【解析】关于问题所求的是我国人口增长速度，材料中无直接相关数据，但是“人均用水量”中涉及人口指标，是两数之比的形式，且“比上年增长0.6%”，即现期与基期比，两数之比(平均数)上升，所以可以得到qa>qb。总用水量看作A，我国人口看作B，材料中已知“全年总用水量比上年增长1.1%”，即qa=1.1%，所以2018年全年我国人口增长速度(qb)小于1.1%，故正确。

通过上述题目可知，已知两数之比的变化，反推增长率的大小关系，其本质考点与已知增长率的大小关系判断两数之比的变化一致，难度不大。但是隐蔽性很强，放在整套题中“藏”得很深，使考生很难发现。因此考生平时需要注重积累，多加练习，增强敏感性。

行测资料分析：乘除变加减——错位加减计算增长量

题型示例

但是常规算法需要计算乘除法，计算难度较高。如何巧妙地避免计算复杂的乘除法，转而计算较简单的加减法呢？

通过观察上式，我们可以发现在不考虑小数点的情况下近似看成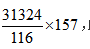此时157和116两个数较为接近，如果能近似地化为相同的数即可约掉，即在116的基础上加上41。但为了保证分数值不变，则需要分子分母同时扩大相同的倍数。下面政华公考就具体来研究如何通过加减来实现分子分母同时扩大或缩小。

方法原理

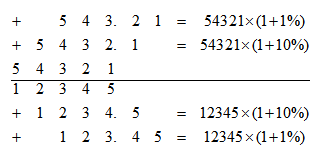
上式中，当分母加上1234.5相当于将分母扩大为(1+10%)倍，则分子也要扩大相同的倍数，则相当于在分子上加了5432.1。同理，如果分母上加123.45则分子上加543.21。

为了简化这一操作，我们采取了保留原式的前三位有效数字的方式，如下式：

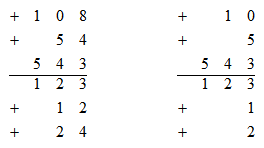
通过观察可得到结论：当分母加上或减去首两位的倍数时，分子也需要加上或减去其首两位相应的倍数；当分母加上或减去首一位的倍数时，分子也需要加上或减去其首一位相应的倍数。但我们常见的情况也并非刚刚好都是首两位或者首一位的倍数，如下式：

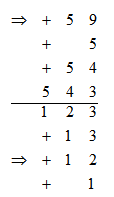
对于这种情况我们可以利用首两位以及首一位的倍数凑出我们想要的数，进而将分子作相应的变化即可。上式中，我们将分母加上的13看成先加12再加1，所以分子上对应要先加54再加5，即加59。

总结口诀：错相同位，加减相同倍。

所以利用以上方法计算例1步骤如下：

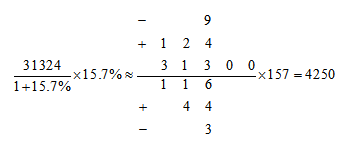
方法应用

例题：截至2021年年底，全国60周岁以上老年人口24949万人，占总人口的17.9%，其中享受高龄补贴的老年人2682.2万人，比上年增长13.9%。

问题：2021年年底，我国享受高龄补贴的老年人口同比增加多少万人？（）

A.271 B.304 C.327 D.355

【答案】C【解析】由材料可知，2021年享受高龄补贴的老年人2682.2万人，比上年增长13.9%。所求为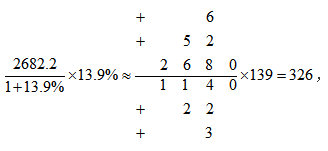选择最接近的C。

通过以上讲解，对于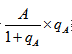类型的计算，我们就可以利用上述错位加减的方法估算。在日常备考过程中也需要大家多加练习，才能真正地将这个算法运用自如。