
行测资料分析增长知识点梳理
行测隔年增长是如何“隔”出来的
在行测考试中,资料分析属于常见题型,题目难度不是非常大,但如果不系统的备考,会出现题目虽会做但耗时长,正确率也不是那么高的情况。所以,资料分析了解题型、掌握方法很重要。今天,就带着大家一起来学习资料分析中的一类题型——“隔年增长”。
一、含义
什么是隔年增长:现期与基期之间隔了一个时间点,去求解增长的相关问题就是隔年增长。现期与基期之间的时间点称为间期,现期的增长率用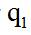 表示,间期的增长率用
表示,间期的增长率用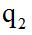 表示,隔年增长率用
表示,隔年增长率用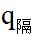 表示。模型如下图所示:
表示。模型如下图所示:
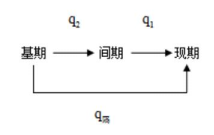
二、常考考点
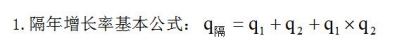
【例1】2020年,互联网企业信息服务收入共7068亿元,同比增长11.5%,增速低于上年同期11.2个百分点。互联网接入及相关服务收入447.5亿元,同比增长11.5%,增速低于上年同期20.8个百分点;互联网数据服务(包括云服务、大数据服务等)收入199.8亿元,同比增长29.5%,增速较上年同期提高3.9个百分点。
问题:2020年,互联网数据服务收入比2018年增加了不到70%。(判断正误)
【答案】正确【解析】根据材料可知,2020年,互联网数据服务收入199.8亿元,同比增长29.5%,增速较上年同期提高3.9个百分点,2019年同比增长29.5%-3.9%=25.6%,所求为29.5%+25.6%+29.5%×25.6%≈29.5%+25.6%+30%×26%=62.9%,不到70%,正确。
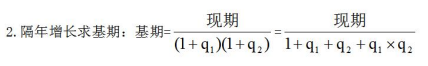
【例2】2015年国民经济和社会发展统计公报显示,全年全国居民人均可支配收入21966元,比上年增长8.9%,增长率比2014年下降1.2个百分点。按常住地分,2015年城镇居民人均可支配收入31195元,比上年增长8.2%,增长率比2014年下降0.8个百分点;农村居民人均可支配收入11422元,比上年增长8.9%,增长率比2014年下降2.3个百分点。全年农村居民人均纯收入为10772元。
问题:2013年,城镇居民人均可支配收入约为多少万元?( )
A.1.9 B.2.2 C.2.6 D.3
【答案】C【解析】根据材料可知,2015年城镇居民人均可支配收入31195元,比上年增长8.2%,增长率比2014年下降0.8个百分点。2014年城镇居民人均可支配收入同比增长8.2%+0.8%=9%,2015年城镇居民人均可支配收入较2013年增长8.2%+9%+8.2%×9%≈17.2%+8%×9%=17.92%。所求为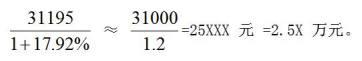 故本题选C。
故本题选C。
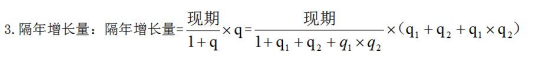
【例3】2019年1-12月份,全国房地产开发投资132194亿元,比上年增长9.9%,增速比上年加快0.4个百分点。其中,住宅投资97071亿元,增长13.9%,增速比上年加快0.5个百分点。2019年,商品房销售面积171558万平方米,比上年下降0.1%。其中,住宅销售面积增长1.5%,办公楼销售面积下降14.7%,商业营业用房销售面积下降15.0%。商品房销售额159725亿元,增长6.5%,增速比上年回落5.7个百分点。其中,住宅销售额增长10.3%,办公楼销售额下降15.1%,商业营业用房销售额下降16.5%。
问题:2019年全国房地产开发投资比2017年增长:( )
A.28114亿元 B.11427亿元 C.22398亿元 D.10278亿元
【答案】C【解析】根据材料可知,2019年全国房地产开发投资132194亿元,比上年增长9.9%,增速比上年加快0.4个百分点。则2018年全国房地产开发投资额的同比增速为9.9%-0.4%=9.5%,2019年全国房地产开发投资额较2017年增长9.9%+9.5%+9.9%×9.5%≈19.4%+10%×10%=20.4%,所求约为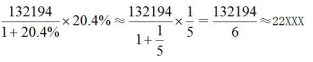 亿元。故本题选C。
亿元。故本题选C。
通过以上三道例题我们可以了解到隔年增长的一些知识点。首先是隔年增长率的求解,其次是隔年增长里求基期值,最后求隔年增长量。最后还是想给大家强调一下,隔年增长里的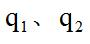 是三个时间里离我们最近的两年的增长率。我们说除了隔年增长外,还有一个年均增长。而年均增长在考试中是如何呈现的呢?我们又需要掌握哪些知识点呢?如果大家想了解更多的内容,请继续关注。
是三个时间里离我们最近的两年的增长率。我们说除了隔年增长外,还有一个年均增长。而年均增长在考试中是如何呈现的呢?我们又需要掌握哪些知识点呢?如果大家想了解更多的内容,请继续关注。
行测资料分析特殊的增长——隔年增长
增长是行测资料分析中一个最基础的知识点,题目类型也较多,其中包含增长、隔年增长、年均增长等。接下来主要给大家介绍一下隔年增长。
一、基本概念及公式
问题:2020年我国棉花产量为M,增长率为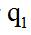 ,上年同期的增长率为
,上年同期的增长率为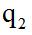 ,问2020年我国棉花产量比2018年增长了百分之几?
,问2020年我国棉花产量比2018年增长了百分之几?
此问题求的是2020年比2018年的增长率,中间隔了一年(2019年),这就是隔年增长率。
我们一般把2020年定义为“现期”,2019年定义为“间期”,2018年定义为“隔年基期”。现期比间期(即2020年比2019年)增长率用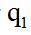 表示,间期比隔年基期(即2019年比2018年)增长率用
表示,间期比隔年基期(即2019年比2018年)增长率用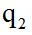 表示。
表示。
【公式推导】
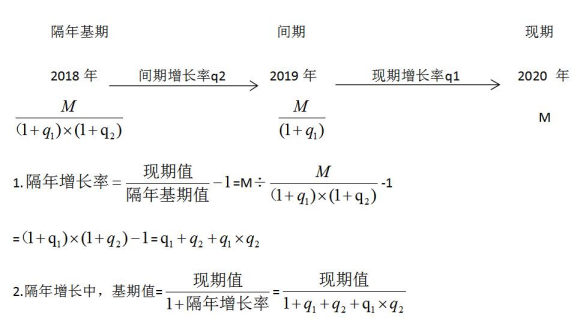
二、例题展示
【例1】2010年上半年,全国原油产量9848万吨,同比增长5.3%,与去年同期提高了6.3个百分点。进口原油11797万吨(海关统计),增长30.2%。原油加工量20586万吨,增长17.9%,增速同比加快16.4个百分点。成品油产量中,汽油产量增长6%,同比减缓7.9个百分点;柴油产量增长28.1%,同比加快15.8个百分点。
问题:求2010年上半年全国原油量比2008年同期约增长了百分之多少?( )
A.1.8% B.4.2% C.6.3% D.9.6%
【答案】B【解析】【解析】问题求的是 2010 年上半年全国原油量比 2008 年同期的隔年增长率,2010

【例2】2015年长沙市国有控股企业实现利润总额134.74亿元,比上年下降16.2%,降幅收窄3.5个百分点。
问题:2013年长沙市国有控股企业实现利润总额为多少亿元?( )
A.168.56 B.189.30 C.221.21 D.246.86
【答案】C【解析】已知 2015 年的利润总额求 2013 年的利润总额,中间间隔 2014 年,所求

三、公式总结

隔年增长问题并不复杂,只要大家掌握隔年增长的含义,并熟练运用隔年增长率以及隔年基期值的计算公式,就可以游刃有余应对这类问题。
行测资料分析:贡献率和拉动…增长
在行测考试中,资料分析是得分的重点题型。除了常规考点外,资料分析有时也会考查一些非常规考点,往往让考生措手不及。今天,特地为大家介绍贡献率和拉动…增长,助力备考。
一、概念
1.贡献率:一般指整体中某部分的增长量对于整体增长的作用大小,实际考查整体中某部分的增长量占整体增长量的比重。各部分贡献率之和等于1,贡献率可正可负,可能超过100%。
2.拉动…增长:用于分析某部分的增长量拉动整体增长程度的指标,一般指整体中某部分的增长量与整体基期值的比值。
二、公式

三、例题展示
【例1】2020年,全国房地产开发投资141443亿元,同比增长7.0%,比上年回落2.9个百分点。其中,住宅投资104446亿元,同比增长7.6%,比上年回落6.3个百分点。
2020年,东部地区房地产开发投资74564亿元,同比增长7.6%;中部地区投资28802亿元,同比增长4.4%;西部地区投资32654亿元,同比增长8.2%;东北地区投资5423亿元,同比增长6.2%。
问题①:2020年,住宅投资对全国房地产开发投资的贡献率为多少?( )
A.73.1% B.79.3% C.85.2% D.89.5%
【答案】B【解析】


问题②:2020年,住宅投资拉动全国房地产开发投资增长多少个百分点?( )
A.3.2个百分点 B.4.5个百分点 C.5.6个百分点 D.6.3个百分点
【答案】C【解析 】


贡献率和拉动…增长,除考查基本公式外,也会考查公式变形,建议熟记基本公式,平时多加练习,从而在考试时能准确识别出考点。
行测资料分析:平均数增长率题型你算得快吗?
一、什么是平均数增长率问题
题目中关于求现期平均数相对于基期平均数增长百分之几的问题就是平均数增长率问题。
平均数增长率的常考公式有
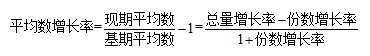
那我们下面就一起来看一看,在实际题目中的应用。
二、常见例题
【例1】2018年前三季度,S省社会物流总额35357.26亿元,同比增长6.4%,增速比上半年放缓0.7个百分点。其中,工业品物流总额16636.15亿元,同比增长0.2%,增速比上半年放缓2.1个百分点。2018年前三季度,S省社会物流总费用2682.1亿元,同比增长6.3%,比上半年放缓0.9个百分点。其中,物流运输环节总费用1854.6亿元,同比增长6.3%。
问题:2018年前三季度,平均每万元社会物流总额产生的物流费用比上年同期:( )
A.下降了不到1% B.下降了1%以上 C.上升了不到1% D.上升了1%以上
【答案】A【解析】问题所求为现期平均数比上年上升/下降百分之几,为平均数增长率考点。由材料可知,2018年前三季度,S省社会物流总额同比增长6.4%;S省社会物流总费用同比增长6.3%。由于S省社会物流总费用的增长率小于S省社会物流总额的增长率,所以平均每万元社会物流总额产生的物流费用比上年同期下降了,排除C、D项;下降了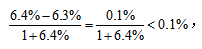 所以下降了不到1%,选择A项。
所以下降了不到1%,选择A项。
【例2】
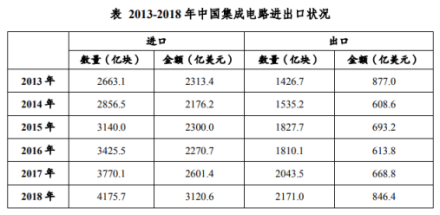
问题:2018年中国平均每块集成电路出口单价比上年:( )
A.上升了30%以内 B.上升了30%以上
C.下降了30%以内 D.下降了30%以上
【答案】A【解析】

通过对比以上两种方法发现,第二种方法明显计算量更小。
三、小结
1.如果题目中直接给出总量增长率和份数增长率,可以直接代入第二个公式。先计算分子判断正负确定上升或者下降,排除选项。再结合分母,选择比分子稍大或者稍小的数据。
2.如果题目中没有直接给出总量增长率或份数增长率,可以先简单估算出增长率的大小,再代入第二个公式求解。
通过以上几道例题,相信同学们已经对平均数增长率了一定的了解,希望大家可以在做题的过程中熟悉这种题型并快速求解。








