政华教育

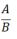
【例1】2021年前三季度，分行业类别营业收入情况：新闻信息服务9847亿元，同比增长22.1%；内容创作生产17693亿元，同比增长18.6%；创意设计服务13787亿元，同比增长24.0%；文化传播渠道9309亿元，同比增长30.1%；文化投资运营359亿元，同比增长13.8％；文化娱乐休闲服务916亿元，同比增长35.3％；文化辅助生产和中介服务11441亿元，同比增长18.3％；文化装备生产4880亿元，同比增长17.8％；文化消费终端生产15974亿元，同比增长22.0％。

2021年前三季度，分行业类别中，同比增速最高行业营业收入是同比增速最低行业营业收入的：（）

A.2倍多 B.3倍多 C.20多倍 D.30多倍

【答案】A【解析】第一步，本题考查倍数问题中的现期倍数计算。

第二步，定位文字材料。增长率最高的为文化娱乐休闲服务（35.3%），对应的营业收入为916亿元；增长率最低的为文化投资运营（13.8%），对应的营业收入为359亿元。

第三步，根据倍数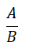＝，代入数据，则同比增速最高行业营业收入与同比增速最低行业营业收入的比值为916÷359≈2.6，即2倍多。

因此，选择A选项。

需要注意的是，如果题目设问是“……比……多/高/超出多少倍？”，则计算公式为：。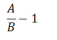

二、基期倍数问题

基期倍数问题，顾名思义需要先一步计算基期量，然后再观察倍数关系。一般来说，材料中已知现期量和增长率来求基期的情况比较常见，所以基期倍数关系相当于两个相除，从而得出的基期倍数核心公式为：。

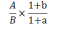【例2】2020年某市实现社会消费品零售总额833.82亿元，同比增长7.0％。按消费形态分，批发和零售业实现713.67亿元，同比增长6.1％；住宿和餐饮业实现120.15亿元，同比增长12.3％。按经营所在地分，城镇实现653.54亿元，同比增长7.2％；乡村实现180.28亿元，同比增长5.9％。

2019年，该市城镇消费品零售总额是乡村消费品零售总额的：（）

A.不到2倍 B.2倍—3倍之间

C.3倍—4倍之间 D.超过4倍

【答案】C【解析】第一步，本题考查基期量和倍数相关知识。

第二步，根据文段材料“2020年某市实现社会消费品零售总额833.82亿元”“按经营所在地分，城镇实现653.54亿元，同比增长7.2％，乡村消实现180.28亿元，同比增长5.9％。”

第三步，根据基期倍数公式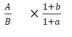，代入数据得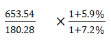，观察式子右边略小于1，左边取整直除，即基期倍数取值在３倍—４倍之间，Ｃ项符合。

因此，选择Ｃ选项。

三、间隔倍数问题

凡是“间隔”问题一般都涉及三个时间点，例如已知2022年和2021年的关系，求2022年与2020年的关系。所以间隔倍数问题的设问方式一般是：今年XX是前年的……倍？间隔倍数看似复杂，但其实材料中会给出连续两年的增长率，这样利用间隔增长率公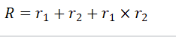，求出R间隔增长率后，再计算R+1，即是间隔倍数。

【例3】2013年3月末，金融机构人民币各项贷款余额65.76万亿元，同比增长14.9%，增速比上年同期低0.8个百分点。

2013年3月末，金融机构人民币各项贷款余额约是2011年同期的多少倍（）？

A.1.1 B.1.2 C.1.3 D.1.4

【答案】C【解析】第一步，本题考查间隔倍数计算。

第二步，定位材料，“2013年3月末，金融机构人民币各项贷款余额65.76万亿元，同比增长14.9%，增速比上年同期低0.8个百分点”。

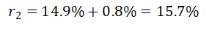
第三步，根据公式，间隔增长率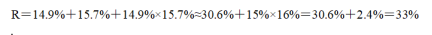，，代入公式得，R＝14.9%＋15.7%＋14.9%×15.7%≈30.6%＋15%×16%＝30.6%＋2.4%＝33%。根据公式，增长率=（现期量-基期量）/基期量=现期量/基期量-1，则现期量/基期量=1+增长率，代入公式得，2013年3月末，金融机构人民币各项贷款余额约是2011年同期的倍数＝1＋33%＝1.33倍。与C选项最接近。

因此，选择C选项。

翻番问题中的“近”“多”“约”

行测资料分析倍数问题中，有一个大家在生活中很熟悉，但是在考试中容易忽略细节的小概念：翻番。一起跟学习一下吧。

概念

翻番是表示数量成倍增长，与“翻”一起构成翻“几番”的表达形式。

注意：“翻番”衡量的往往是同一统计量在两个时期的对比，不能说两个不同的统计量A比B翻了几番。

例题：2000年中国每月实际平均工资为832元，2009年为2440元。

问题：2009年，我国每月实际平均工资比2000年翻了几番？

【解析】2440÷832≈3倍，大于2倍，小于4倍，翻了一番多。

翻番问题中的易错点

翻番是与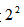相关联，翻的番数越多，n-1与n之间差的倍数就越多，而倍数却是一个相对精确的数值，所以就给了出题人玩弄文字游戏的空间，最常见的就是在翻n番的边缘，用不同的字眼之间微小的差距来给考生“挖坑”，那在翻番问题中，都有哪些字眼需要去注意呢？

①“近”

例1:2016年至2020年中国冻牛肉进出口总量依次为577359吨、689475吨、1023828

吨、1622220吨、2069654吨。其中冻牛肉出口总量依次为4143吨、918吨、429吨、207吨、97吨。

问题：与2016年相比，2020年中国冻牛肉进出口总量翻了近两番。(判断正误)

【答案】正确【解析】由材料可知，2020年中国冻牛肉进出口总量为2069654吨，2016年为577359吨，2069654÷577359≈3.5倍。最接近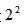，但是又小一点，所以是正确的。

点拨：“近”就是接近的意思，还没有达到但是差的不多，有时也会用“不足X番”，但“不足”也可以不那么接近。

②“多”

例2：1978-2011年，我国农业机械拥有量有了显著提升。1978年农用大中型拖拉机持有量为557358台，小型拖拉机持有量为1373000台，农用机械总动力为11749.9万千瓦。2011年，农用大中型拖拉机持有量为4406471台，小型拖拉机持有量为18112663台，农用机械总动力为97734.7万千瓦。

问题：2011年我国农用大中型拖拉机持有量比1978年翻了三番多。(判断正误)

【答案】错误【解析】由材料可知，2011年，农用大中型拖拉机持有量为4406471台，1978年为557358台，4406471÷557358≈7.9倍，翻了三番多应该大于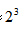=8倍，故本题错误。

点拨：“多”是大于的意思，翻了三番多，就需要超过3番=8倍，但不能大于4番=16倍。

③“约”

例3：1978年我国人均消费牛奶是1.2公斤，2012年我国人均消费牛奶是9.8公斤。

问题：1978-2012年我国人均消费牛奶翻了约三番。(判断正误)

【答案】正确【解析】2012年我国人均消费牛奶是9.8公斤，1978年为1.2公斤，9.8÷1.2≈8.2≈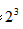，所以翻了约三番。

点拨：“约”是约等于的意思，可以多一点，也可以少一点，但是差得不多。

一字之差，意思大不同，大家在做题的时候，一定要注意问题的细节，避免落入出题人精心设置的“陷阱”之中。

资料分析如何求解隔年倍数

基本概念

隔年倍数求解的是现期值和基期值之间的倍数关系，不过是中间间隔了一个完整的时间单位——年，对于隔年增长率的公式我们十分熟悉，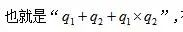

在隔年增长率的基础上加上1不就是隔年倍数嘛。一般而言，题目当中都会直接或者间接给到两个增长率即：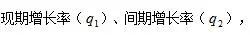

求解现期值是基期值的多少倍。例如：2021年同比增长率q1，2020年同比增长率q2，求2021年是2019年的多少倍？

此时求解的即为隔年倍数。我们知道，普通倍数和增长率之间是有联系的，是几倍=1+增长率，而隔年倍数公式中的增长率为隔年增长率，即隔年倍数=1+隔年增长率。

基本公式

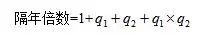
例题1：2013年3月末，金融机构人民币各项贷款余额65.76万亿元，同比增长14.9%，增速比上年同期低0.8个百分点。

问题：2013年3月末，金融机构人民币各项贷款余额约为2011年同期的多少倍（）？

A.1.1 B.1.2 C.1.3 D.1.4

【答案】C【解析】题干中2013年和2011年之间间隔了2012年，且求解两年之间的倍数关系，属于隔年倍数题目。

由题可知，2013年3月末同比增长率为14.9%，增速比上年同期低0.8个百分点，则2012年3月末同比增长率为14.9%+0.8%=15.7%。由隔年倍数公式可知，所求为

1+14.9%+15.7%+14.9%×15.7%≈1.33倍。因此，选择最接近的C选项。

例题2：2014年我国经济在转型升级中步入中高速发展的“新常态”，战略性新兴产业和生产性服务业逆势上行，渐成拉动经济增长的两大“新引擎”。

以发展速度论，新业态快速进入百姓生活，新型服务业攻城略地，势如破竹。

2014年，金融业增加值增速较快，比第三产业增加值增速8.1%快2.1个百分点。电子商务全国网上零售增长赢得最佳绩，比全社会消费品零售总额增速12.0%快37.7个百分点，并拉动快递业务量较上年增长61.6%之后再创51.9%的高增速。

问题：2014年我国的快递业务量约是2012年的多少倍（）？

A.1.8 B.2.1 C.2.5 D.3.3

【答案】C【解析】题干中2014年和2012年之间间隔了2013年，且求解两年之间的倍数关系，属于隔年倍数题目。由题可知，2014年快递业务量较上年增长61.6%之后再创51.9%的高增速。由隔年倍数公式可知，所求为1+61.6%+51.9%+61.6%×51.9%≈2.45倍。因此，选择最接近的C选项。

工欲善其事，必先利其器，

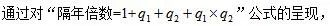
相信大家已经掌握了此公式以及考查方式。再次遇到这种问题时，我们可直接套用“隔年倍数”的公式，对所求问题进行计算求解，从而节约做题时间。