
行测资料分析:基期平均数考点
快速梳理基期平均数
在行测考试中,平均数是资料分析当中重点考察的内容,而其中的基期平均数同时涉及增长和平均数,在梳理数据时有可能导致梳理不清楚。那么怎么解决这个难题呢?今天就带大家一起学习基期平均数。
一、什么是基期平均数
基期平均数的含义:基期总量与基期份数之比。
例如:题目中是2020年全国主要农作物产量和面积的数据,问题:2019年全国主要农作物平均每亩的产量为多少?题目数据是2020年,问题问的是2019年的平均数,也就是需要让我们求解基期平均数。接下来通过几道例题,我们一块来学习。
二、常见考法
1.已知现期值和增长量
【例1】2018年全国粮食产量6.09亿吨,比2017年增加0.44亿吨;全国粮食种植面积17.56亿亩,比2017年增加0.54亿亩。
问题:2017年全国粮食平均每亩的产量为多少吨?
【解析】题目数据是2018年,问题问的是2017年的平均数,也就是求基期平均数,但是已知条件中给出的是现期的总量、份数以及其对应的增长量,可以通过公式:基期值=现期值-增长量。分别得到其对应的基期值。列式为: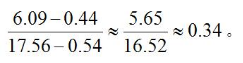
总结:在已知现期值和增长量时,基期平均数的公式:
2.已知现期值和增长率
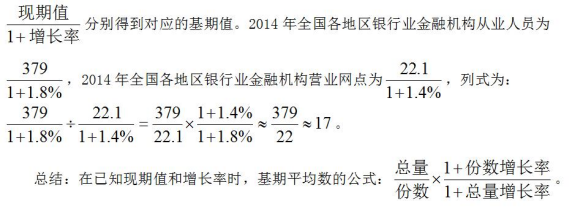
【例2】2015年末,全国各地区银行业金融机构营业网点共计22.1万个,从业人员379.0万人,资产总额174.2万亿元,同比分别增长1.4%、1.8%和12.6%。分地区看,中部、西部和东北地区银行业金融机构发展加快,从业人员和资产规模占全国的比例同比均有所提高,东部地区这两项指标占比同比分别下降1.0个百分点和0.7个百分点。
问题:2014年末,我国银行业金融机构营业网点的从业人员平均规模是多少万人。
【解析】题目数据是2015年,问题问的是2014年的平均数,也就是求基期平均数,但是已知条件中给出的是现期的总量、份数以及对应的增长率,可以通过
3.题目中既有增长量也有增长率
【例3】2017年上半年,S市出口手机1.9亿台,比去年同期增长7.3%;价值1513.1亿元,增长43.2亿元。6月当月出口3217.5万台,减少23.7%;价值86亿元,下降27.8%。
问题:2016年上半年,S市平均每台出口手机的价值为多少亿元
【解析】题目数据是2017年上半年,问题问的是2016年上半年的平均数,也就是求基期平均数,但是已知条件中给出的是现期的总量及其增长量、份数及其增长率,

总结:当题目中既涉及增长量和增长率的时候,一步一步分析,对应着分别求出基期总量和基期份数即可。
通过以上题目,相信考生们对于如何梳理基期平均数有了一定的了解,希望大家可以快速地掌握这种梳理方法,并对其勤加练习,解决基期平均数便会得心应手。
利用公式速求基期两数之比
在行测考试的资料分析专项中,我们常常会碰到类似基期倍数、基期比重、基期平均数等基期两数之比的一些问题,如果一步一步精确计算,比较繁琐。今天和大家一起探索,如何快速求解此类问题。
公式回顾

计算技巧
例1:2016年,J省规模以上工业取水量为86.4亿立方米,比上年增长12.3%。其中,自来水取水量15.9亿立方米,同比增长11.8%,则2016年J省规模以上工业取水量自来水取水量所占的比重为( )?
A.18.5% B.28.4% C.9.2% D.34.5%
【答案】A【解析】本题求基期比重,所求为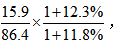 1+12.3%与1+11.8% 接近,故
1+12.3%与1+11.8% 接近,故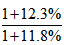 的结果虽大于1但与1比较接近,
的结果虽大于1但与1比较接近,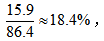 选择大于18.4%同时与18.4%接近的数,故本题选A。
选择大于18.4%同时与18.4%接近的数,故本题选A。
例2:2020年,全省规模以上重工业完成增加值12625亿元,增长28.5%,轻工业完成增加值2527亿元,增长27.9%,则2019年全省规模以上重工业完成增加值是轻工业完成增加值的几倍( )?
A.4.2 B.4.9 C.5.3 D.6.8
【答案】B【解析】本题求基期倍数,所求为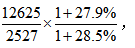 1+27.9%与1+28.5% 接近,故
1+27.9%与1+28.5% 接近,故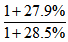 的结果虽小于1但与1比较接近,
的结果虽小于1但与1比较接近,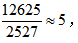 选择小于5同时与5比较接近的数,故本题选B。
选择小于5同时与5比较接近的数,故本题选B。
【点拨】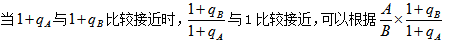 与
与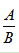 的大小关系结合选项从而确定答案。
的大小关系结合选项从而确定答案。
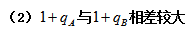
例3:2015末,全国各地区银行业金融机构营业网点共计22.1万个,从业人员379.0万人,资产总额174.2万亿元,同比分别增长10.4%、22.6%和1.8%。则2014年末,我国平均每个银行业金融机构营业网点的从业人员约为多少人( )?
A.16 B.11 C.23 D.29
【答案】A【解析】本题求基期平均数,所求为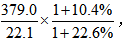 1+10.4%与1+22.6%相差较大,根据前面的方法,无法确定最终结果。此时可按照有效数字法运算顺序,取前两位有效数字进行估算,
1+10.4%与1+22.6%相差较大,根据前面的方法,无法确定最终结果。此时可按照有效数字法运算顺序,取前两位有效数字进行估算,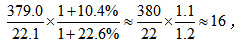 故本题选A。
故本题选A。
【点拨】当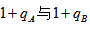 相差较大时,无法跟
相差较大时,无法跟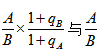 的大小确定答案,可以保留适当有效数字按先加减、后乘、最后除的运算顺序进行取舍估算。
的大小确定答案,可以保留适当有效数字按先加减、后乘、最后除的运算顺序进行取舍估算。
通过上面的练习相信大家对于基期两数之比的计算应该有所了解,建议大家在备考期间多多练习,灵活应变从而提高自己的解题速度。
基期平均数精讲
行测中的资料分析部分是我们在备考中不可忽视的内容。那今天就由带大家一起来回顾一下资料分析中经常出现的一个身影,平均数的相关内容——基期平均数。
基本概念
在资料分析中,一般材料中出现的统计时间我们会分为现期和基期,作为参照标准的时期称之为基期,所以求参照时期的平均数就是基期的平均数也就是我们今天所了解的内容。
基本公式
根据材料中给出的数据,当已知两个统计指标总量和份数的现期值以及对应的增长量的时候,所求为: 当已知两个统计指标总量和份数的现期值以及对应增长率的时候,所求为:
当已知两个统计指标总量和份数的现期值以及对应增长率的时候,所求为: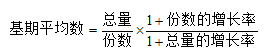 在我们做题的时候,需要注意的是,结合所求的关于基期平均数的问题,迅速找到上述公式中总量、份数指标的有关数据,代入数据,这一过程中要注意数据在公式中对应的位置。那我们可以通过几道例题来练习一下。
在我们做题的时候,需要注意的是,结合所求的关于基期平均数的问题,迅速找到上述公式中总量、份数指标的有关数据,代入数据,这一过程中要注意数据在公式中对应的位置。那我们可以通过几道例题来练习一下。
模拟例题
例题1:2018年,美国对华出口水果11.16万吨,相比2017年减少了4.13万吨;对华出口水果贸易总值2.69亿美元,比2017年减少了1.22亿美元。
问题:2017年美国对华出口水果均价为( )美元/吨。
解析:已知材料描述的是两个指标对华出口水果量和贸易总值关于2018年的数据,以及与2017年相比较增长带单位的量。问题求2017年美国对华水果均价,则为求基期平均数,故根据所给数据可列式为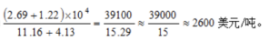
例题2:2018年北京商品住宅销售面积为526.76万平方米,同比减少13.5%;商品住宅销售额为1971.14亿元,同比减少5.1%。
问题:2017年北京商品住宅销售均价为( )万元/平方米。
解析:已知材料描述的是两个指标——北京商品住宅销售面积和销售额——关于2018年的数据,以及与2017年相比较增长不带单位的率。问题求2017年北京商品房住宅均价,则为求基期平均数,故根据所给数据可列式为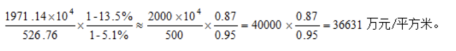
综上所述,大家对于基期平均数公式的熟练运用,重点在于对其基本概念和基本公式的理解,然后通过多做相关题目,来了解不同材料有关数据的表达方式和问题,从而实现对于求解基期平均数这一问题的快速列式。








