
行测资料分析常考知识点
不让时间成为你失分的易错点
行测资料分析题量大、分值高,很多考生却在学习过程中不注重细节而导致失分。接下来带着大家一同去梳理资料分析中关于时间的易错点,让我们在考试中减少不必要的失分。
时间点易错点
1.材料中出现多个时间点,明确问题时间点的对应时间:
例1:2021年1-10月,我国社会消费品零售总额244359亿元,同比增长10.6%。10月当月社会消费品零售总额28279亿元,同比增长11.0%。
问题:2020年10月我国社会消费品零售总额为多少亿元( )?
A.244359 B.28279 C.220939 D.25477
【答案】D【解析】问题时间为2020年10月,明确对应时间为10月当月,即所求为社会消费品零售总额10月当月的基期值。材料给出10月当月现期值28279亿元,同比增长11.0%,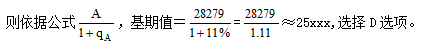
2.材料明确给出的时间点与问题时间点不直接匹配对应,分析材料隐含时间点:
例2:2020年我国试验与研究发展(R&D)经费支出13312亿元,比上年增长12.4%,同比下降2.6个百分点。
问题:2018年我国研究与试验发展(R&D)经费支出为多少亿元( )?
A.10299 B.13312 C.11843 D.12159
【答案】A【解析】材料所给时间为2020年,问题时间为2018年,且材料没有给出2020年与2018年的比较增长率,则不可直接求解。分析材料可知2020年的增长率为12.4%,同比下降2.6个百分点,可得隐含时间点2013年的增长率为12.4%+2.6%=15.0%。则问题所求为我国研究与试验发展经费支出的隔年基期值,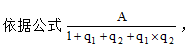 基期值
基期值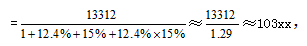 选择A选项。
选择A选项。
时间段易错点
材料所给时间段与问题所求时间段不完全一致
例3:已知2016-2021年我国每年城乡就业人员数,其中,城镇每年就业人员数:32103万人、33322万人、34687万人、35914万人、37102万人、38240万人;乡村每年就业人员数:43461万人、42506万人、41418万人、40506万人、39602万人、38737万人。
问题:2018-2021年我国城镇就业人员数平均每年增长多少万人( )?
A.984 B.888 C.1184 D.1230
【答案】C【解析】问题所求为2018-2021年我国城镇就业人员数平均每年增长多少万人,可知要求年均增长量,材料所给时间为2016-2021年,问题与材料时间段不完全一致,则明确初期值为2018年城镇就业人员数34687万人,末期值为2021年城镇就业人员数38240万人,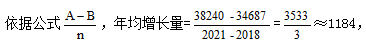 选择C选项。
选择C选项。
资料分析考点——隔年增长
知识引导
隔年增长问题是行测资料分析中的常见考点,作为行测资料分析中的一个重要考点,在国省考行测中出现的频率是相当高的。
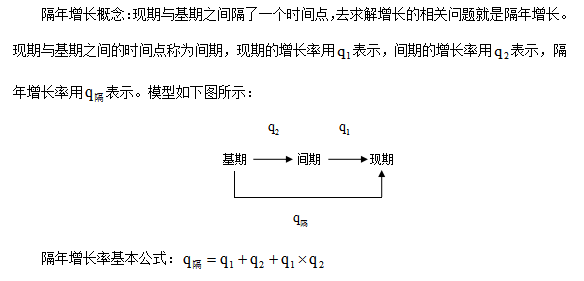
因为多了“隔年”两个字,导致很多早期备考的考生觉得这类题目很难。在此告诉大家一种方法,只要遇到隔年增长问题,就先算隔年增长率。算完隔年增长率之后,隔年增长率问题就转化成了普通增长问题,按照普通增长问题的列式和估算方法进行处理即可。接下来借助几种常见的考法看一看具体怎么操作。
一、单纯考查隔年增长率问题,按照公式q1+q2+q1×q2进行列式求解。
二、隔年增长问题中的基期值:先求出隔年增长率,然后按基期值= 进行求解即可。
进行求解即可。
三、隔年增长问题中求现期值相对于基期值增长量:先求出隔年增长率,按 求解增长量即可。
求解增长量即可。
练习题
例1:2020年底,建筑业从业人数5367万人,比上年下降1.1%,增速同比增加1.3个百分点。全国共有建筑业企业单位数为116716个,比上年增长12.4%,上年为增长7.5%。
问题:2020年底,全国建筑业企业单位数比2018年底增长了:( )
A.22.5% B.20.8% C.12.4% D.7.5%
【答案】B【解析】由材料可知,2020年底,全国建筑业企业单位数比上年增长12.4%,上年为增长7.5%。所求为12.4%+7.5%+12.4%×7.5%≈19.9%+12%×8%=19.9%+0.96%=20.86%,选择最接近的B项。
例2:2020年,全国建筑业企业签订合同总额为59.6万亿元,比上年增长9.3%,同比下降2.5个百分点。其中,本年新签合同额32.5万亿元,比上年增长12.4%,同比增加4.5个百分点。
问题:2018年,全国建筑业企业新签合同额约为多少万亿元( )?
A.26.8 B.29.9 C.32.5 D.36.3
【答案】A【解析】由材料第三段可知,2020年,全国建筑业企业新签合同额32.5万亿元,比上年增长12.4%,同比增加4.5个百分点。则2019年全国建筑业企业新签合同额的同比增速为12.4%-4.5%=7.9%,因此2020年全国建筑业企业新签合同额比2018年增长了12.4%+7.9%+12.4%×7.9%≈20.3%+12%×8%=20.3%+0.96%=21.26%,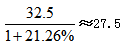 万亿元,选择最接近的A项。
万亿元,选择最接近的A项。
例3:2020年,建筑业固定资产投资2751亿元,比上年增长9.2%。建筑业总产值达到263947亿元,比上年增长6%,同比下降4个百分点。
问题:2020年,全社会建筑业总产值比2018年约增长:( )
A.37577亿元 B.30147亿元 C.23995亿元 D.14940亿元
【答案】A【解析】由材料可知,2020年全社会建筑业总产值达到263947亿元,比上年增长6%,同比下降4个百分点。则2019年全社会建筑业总产值比上年增长6%+4%=10%,则2020年全社会建筑业总产值比2018年增长6%+10%+6%×10%=16%+0.6%=16.6%,所求为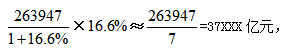 选择A项。
选择A项。
常见两数之比的概念
一、基础概念
1.产销率(工业产品销售率)是指工业企业在一定时期已经销售的产品总量与可供销售的工业产品总量之比。产品销售率是指报告期产品销售量与产品生产量的比率。是反映报告期工业企业产品产销衔接情况,反映产品生产、销售、流通及满足社会需要程度的指标。产销率越大,说明产品在生产领域和流通领域中存留的时间越少,资金周转越快。
2.利润率反映企业一定时期利润水平的相对指标。利润率指标既可考核企业利润计划的完成情况,又可以比较各企业之间和不同时期的经营管理水平,提高经济效益。
毛利率又称销售毛利率,是一个衡量盈利能力的指标,通常用百分数表示。一般情况下毛利率越高则说明企业的盈利能力越高,控制成本的能力越强。
二、基本公式
1.产销率(%)=工业销售产值/工业总产值(现价)×100%
2.成本利润率=利润÷成本×100%
销售利润率=利润÷销售×100%
毛利率=(主营业务收入-主营业务成本)利润÷主营业务收入×100%
三、经典例题
例1:2021年1-10月,我国某汽车产业生产汽车63941辆,销售47258辆。10月当月生产汽车5932辆,销售3258辆。
问题:2021年1-9月,该汽车产业汽车的产销率为多少( )?
A.59% B.69% C.72% D.76%
【答案】D【解析】根据材料可知,2021年1-9月的产量、销量分别为1-10月的产量、销量减掉10月当月的产量、销量,则列式为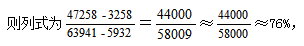 选择D选项。
选择D选项。
例2:2020年,我国规模以上工业企业实现主营业务收入133.12万亿元,比上年增长12.4%,同比下降2.6个百分点。发生主营成本96.3万亿元,增长21.4%;实现利润总额80001亿元,同比增长14.1%。
问题:相比上一年,2020年我国规模以上工业企业实现主营业务收入的利润率( )?
A.上升不足2个百分点 B.上升超过2个百分点
C.下降不足2个百分点 D.下降超过2个百分点
【答案】A【解析】由材料可知,我国规模以上工业企业实现主营业务收入133.12万亿元,比上年增长12.4%;实现利润总额80001亿元,同比增长14.1%。则所求为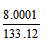
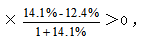 即利润率上升,排除C、D;上升了
即利润率上升,排除C、D;上升了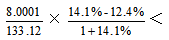 14.1%-12.4%=1.7%,即上升了不足1.7个百分点,选择A选项。
14.1%-12.4%=1.7%,即上升了不足1.7个百分点,选择A选项。
隔N年的增长率如何求解
隔年增长作为行测资料分析中的一个重要考点,在国省考行测中出现的频率是相当高的。某些省考中关于隔年增长的考查十分具有创新性,不是简单的考查隔一年的增长率,而是考查隔N年的增长率。隔一年的增长率的相关公式我们比较熟悉,在实际考试中直接带公式就可以求解,难度不大。今天通过两道题告诉大家隔N年的增长率如何求解?
例1:
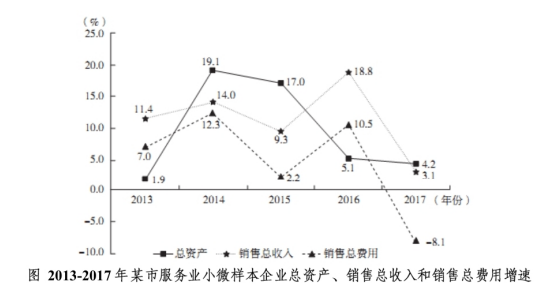
问题:2017年该市服务业小微样本企业销售总收入比2013年增长:( )
A.100%-3.1%×18.8%×9.3%×14.0%
B.103.1%×118.8%×109.3%×114.0%-100%
C.100%-3.1%×18.8%×9.3%×14.0%×11.4%
D.103.1%×118.8%×109.3%×114.0%×111.4%-100%
【答案】B【解析】这道题目要求的是2017年比2013年的增长率,现期是2017,基期是2013,中间隔4年,所以是求隔4年的增长率。需要注意的是,无论是隔几年,本质上就是求增长率,所以只需要利用增长率的基本公式求解即可, 由折线图中每年该市服务业小微样本企业销售总收入的同比增速可知,2017年的数值可利用现期值=基期值×(1+增长率)表示为2013年数值×114.0%×109.3%×118.8%×103.1%,则2017年相较2013年增长了2013年数值×114.0%1×09.3%×118.8%×103.1%÷2013年数值-1=114.0%×109.3%×118.8%×103.1%-100%。故本题选B。
由折线图中每年该市服务业小微样本企业销售总收入的同比增速可知,2017年的数值可利用现期值=基期值×(1+增长率)表示为2013年数值×114.0%×109.3%×118.8%×103.1%,则2017年相较2013年增长了2013年数值×114.0%1×09.3%×118.8%×103.1%÷2013年数值-1=114.0%×109.3%×118.8%×103.1%-100%。故本题选B。
例2:
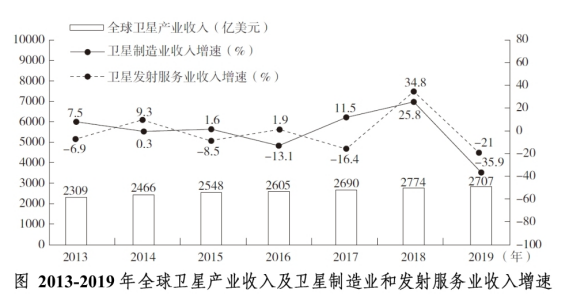
问题:以2012年为基期,2019年全球卫星制造业、卫星发射服务业的收入增长情况分别是:( )
A.负增长、正增长 B.负增长、负增长
C.正增长、负增长 D.正增长、正增长
【答案】B【解析】这道题目要求的是2019年比2012年的增长率,现期是2019年,基期是2012年,中间隔7年,所以是求隔7年的增长率。需要注意的是这道题本质上就是求增长率,所以只需要利用增长率的基本公式求解即可, 由折线图可知,2019年全球卫星制造业收入较2012年的增长率为(1-35.9%)×(1+25.8%)×(1+11.5%)×(1-13.1%)×(1+1.6%)×(1+0.3%)×(1+7.5%)-1,其中(1+11.5%)×(1-13.1%)×(1+1.6%)=(1-13.1%)×(1+1.6%+11.5%+0.1X%)=(1-13.1%)×(1+13.1%+0.1X%)<1,同理分析剩余部分(1-35.9%)×(1+25.8%)×(1+0.3%)×(1+7.5%)也小于1,所以原式<0。即实现负增长。2019年全球卫星发射服务业收入较2012年的增长率为(1-21%)×(1+34.8%)×(1-16.4%)×(1+1.9%)×(1-8.5%)×(1+9.3%)×(1-6.9%)-1,其中(1-21%)×(1+34.8%)×(1-16.4%)<1,剩余部分(1+1.9%)×(1-8.5%)×(1+9.3%)×(1-6.9%)<1,所以原式<0。即实现负增长。符合题意的是B,故本题选B。
由折线图可知,2019年全球卫星制造业收入较2012年的增长率为(1-35.9%)×(1+25.8%)×(1+11.5%)×(1-13.1%)×(1+1.6%)×(1+0.3%)×(1+7.5%)-1,其中(1+11.5%)×(1-13.1%)×(1+1.6%)=(1-13.1%)×(1+1.6%+11.5%+0.1X%)=(1-13.1%)×(1+13.1%+0.1X%)<1,同理分析剩余部分(1-35.9%)×(1+25.8%)×(1+0.3%)×(1+7.5%)也小于1,所以原式<0。即实现负增长。2019年全球卫星发射服务业收入较2012年的增长率为(1-21%)×(1+34.8%)×(1-16.4%)×(1+1.9%)×(1-8.5%)×(1+9.3%)×(1-6.9%)-1,其中(1-21%)×(1+34.8%)×(1-16.4%)<1,剩余部分(1+1.9%)×(1-8.5%)×(1+9.3%)×(1-6.9%)<1,所以原式<0。即实现负增长。符合题意的是B,故本题选B。
通过上述例题相信大家会发现隔N年增长率本质依然是增长率,只需要利用增长率的基本公式求解即可。需要注意的是有时候题干并不会告诉我们现期值、基期值,而是通过折线图的形式告诉我们每一年的增长率。这个时候我们只需要利用现期值=基期值×(1+增长率)表示出现期值,然后再利用增长率=-1进行求解。








