行测资料分析：增长中的隔年

行测资料分析考查增长这个概念时，会有一个知识的延伸，由普通增长考查到隔年增长内容。但是具体隔年增长会考查什么呢?包含隔年增长率、隔年倍数以及隔年增长中求基期值，其中以隔年增长率为主：隔年增长率的计算需要从概念分析，列最简单的式子进行计算并掌握简单的计算方法，这样才能在确保计算准确率的前提下尽可能的节省考试时间，准确完成题目。下面就给大家讲解隔年增长的相关知识点：

一、隔年增长率

假设2017年的棉产同比增长率为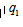，2016年的棉产同比增长率为，2015年的棉花产量为。如果问题所求为2017年棉花产量较2015年棉花产量增长了百分之几?这样的题目就是求隔年增长率(现期和基期之间间隔一个统计周期)。根据现期值=基期值×(1+增长率)，可以推出2016年的棉花产量为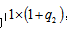。求为2017年棉花产量较2015年棉花产量增长了百分之几，可以用增长率的公式：现期值/基期值-1来求解。化简可以得到隔年增长率为中间间隔时期增长率。

例1.

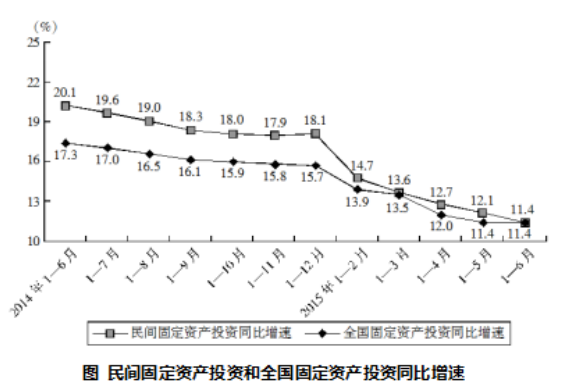
问题：与2013年上半年相比，2015年上半年全国固定资产投资约上升了：

A.11.4% B.17.3% C.28.7% D.30.7%

【答案】 C解析：2015年上半年全国固定资产投资同比增长率为11.4%，2014年上半年为17.3%，则所求为11.4%+17.3%+11.4%×17.3%>11.4%+17.3%=28.7%，符合题意的是C项。

二、隔年基期值

已知现期值与两个增长率，求隔年基期的值。根据增长公式可以推出：基期=现期值/1+增长率，隔年基期值=现期值/(1+隔年增长率)，。

例2. 2016年，我国东部地区民间固定资产投资164674亿元，比上年增长6.8%;中部地区107881亿元，比上年增长5.9%，增速回落0.1个百分点;西部地区71056亿元，比上年增长2.4%，增速回落0.5个百分点;东北地区21608亿元，比上年下降24.4%，降幅收窄1.6个百分点。

问题：东北地区2014年民间固定资产投资额为：

A.28582亿元 B.29200亿元

C.35864亿元 D.38624亿元

【答案】D解析：由材料可知，2016年东北地区固定资产投资额为21608亿元，比上年下降24.4%，降幅收窄1.6个百分点，则所求为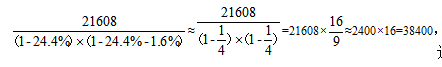选择最接近的D项。

行测数量关系：巧解和定最值问题

行测考试中数量关系这部分的题目很多同学会很纠结，如果每道题都做，那么整体时间会不够;如果一道题都不做，只靠“感觉”去蒙，那么又会影响到行测考试的整体分数。所以，我们一般会建议大家用10分钟的时间去挑3-4道，再根据做出来的选项去“蒙”，正确率会高很多。那么，在这有限的10分钟里我们要挑什么什么样的题做呢?今天要讲的和定最值问题，会是一个不错的选择。

1.什么是和定最值

和定最值，顾名思义，在和一定的条件下求解最值的问题。让我们来通过一道例题，来看看和定最值的题型特征。

例题：在一场百分制的考试中，5个人的总分是330分，这5个人都及格了，而且每个人成绩是互不相等的整数。那么成绩最好的最多得几分?

首先我们去看题干，“5个人的总分是330分”意思是这5个人的成绩和是一个定值，也就是“和定”，问的是“成绩最好的最多得几分”求得是其中一个人所得成绩最大值，也就是“最值”，属于和定最值的题型特征。

2.解题原则

对于和定最值问题的解题原则是：当总和一定的情况下，若要求其中某个量的最大值，其他量应该尽可能小，若要求其中某个量的最小值，其他量应该尽可能大。解题方法主要就是设未知数，根据题目列方程求解。

3.方法运用

例题：在一场百分制的考试中，5个人的总分是330分，这5个人都及格了，而且每个人成绩是互不相等的整数。

问题1：成绩最好的最多得几分?

【解析】题目中提到每个人是互不相等的整数，所以我们可以将5人成绩按照从大到小进行排序。根据解题原则，5人成绩总和是330，成绩最好的人得分要尽可能地多，那其余4人得分要尽可能小，而且每个人都及格且是互不相等的整数，进而可以推出第五名成绩为60，第四名成绩要比第五名多，还得尽可能小，那么就比第五名多1分，也就是61，以此类推，第三名成绩为62，第二名成绩为63。设第一名成绩为X，可列方程：X+63+62+61+60=330，解得X=84，因此成绩最好的最多得84分。

问题2：成绩最差的最多得几分?

【解析】依然将5人成绩按照从大到小进行排序。根据解题原则，5人成绩总和是330，成绩最差的人得分要尽可能地多，那其余4人得分要尽可能小，而且每个人都及格且是互不相等的整数，我们会发现成绩好的人分数要尽可能的低，成绩差的人成绩反而要尽可能的高，每个人都不好确定，那不妨就问谁设谁，设第五名最多为X，那么第四名成绩要比第五名高，要尽可能的低，还得是整数，那么就比第五名多1分，也就是X+1，以此类推，第三名成绩为X+2，第二名成绩为X+3,第一名成绩为X+4，可列方程：X+4+X+3+X+2+X+1+X=330，也就是5X+10=330,解得X=64，因此成绩最差的最多得64分。

问题3：若第一名成绩不超过70，则成绩第三的最少得几分?

【解析】同样的条件下，依旧将5人成绩按照从大到小进行排序。根据解题原则，5人成绩总和是330，成绩第三的人得分要尽可能地少，那其余4人得分要尽可能多，而且每个人都及格且是互不相等的整数，我们可以先把能够确定的先确定下来。第一名要尽可能地多，而且不超过70，那么第一名最多就是70分，第二名要比第一名分少，还得是尽可能的大的整数，那么第二名就比第一名少1分，也就是69，第三名是我们要求的，不妨设第三名最少为X，那么第四名成绩要比第三名低，还得是尽可能高的整数，那么就比第三名少1分，也就是X-1，以此类推，第五名成绩为X-2，可列方程：70+69+X+X-1+X-2=330，解得X≈64.67，因为每个人都是整数，这里的X是第三名最少的得分情况，第三名最少是64.67，分数不能比64.67更少，所以需要向上取整为65分。

以上就是对和定最值基础题型的一些分析，大家掌握好解题原则之后，多多练习，和定最值将会是帮助我们得分的一类问题。

行测技巧：排列组合题真的是行测“杀手”吗?

排列组合是公职考试中的常考题型，也是完完全全的高中知识考查。很多人觉得其抽象难懂，每次遇到都是看运气能不能蒙对了。但排列组合题真的就是行测“杀手”，遇到之后只能拼运气吗?显然不是，今天就来带各位考生学习易拿分的排列组合题――隔板模型。

一、应用环境

隔板模型主要用来解决同素分堆问题，所谓的同素分堆指的是相同的元素分组问题。比如：将5个苹果分给3个小朋友，每个小朋友至少分得一个的方法数有多少种?对于这样的问题我们有一个一般性的问题描述：把n个相同元素分给m个不同对象，每个对象至少分得1个元素的方法数有多少种?

二、方法介绍

隔板模型的做法：在n个相同元素的n―1个间隙中插入m―1个板，将其分为m组。根据板的插入位置不同，既可以考虑到所有分类情况，也能兼顾到至少一个的特殊要求。由于每个板都是一样的，所以不考虑顺序，结果数记为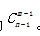。当然，有时候题干中要求的每个对象不一定是至少分得1个元素，所以会有条件的变形，但并不影响我们的方法使用。

下面我们就来感受下隔板模型解决的一些基本问题和变形问题。

三、模型应用

例1.某单位订阅了6份学习材料发放给4个部门，每个部门至少发放一份材料。问一共有多少种不同的发放方法?

A.9 B.10 C.11 D.12

【解析】选B。题干中学习材料是相同元素，部门为不同对象，每个对象至少分得一个，属于同素分堆一般性问题描述，所以直接套结论即可。在6个元素的5个间隙中插入3个板分给4个对象，即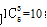，选B。

例2.某单位订阅14份学习材料发放给4个部门，每个部门至少发放3份材料。问一共有多少种不同的发放方法?

A.9    B.10     C.11     D.12

【解析】选B。题干中学习材料是相同元素，部门为不同对象，属于同素分堆问题。但题干要求每个部门至少3份，不是一般性问题描述，属于变形题。所以不能直接套用公式，那么需要问题转化，至少3份=至少1份+2份。第一步，每个部门先分2份，由于材料一样，所以分法就一种。这样还剩下14-4×2=6份;第二步，将剩下的6份分给4个部门，保证每个部门至少一份，即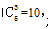;第三步，由于每个部门先分了2份，再加上第二步的每个部门至少一份，这样就可以保证每个部门至少3份了，所以分步相乘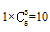，选B。

提醒各位考生，以上就是关于隔板模型的基本型以及变形问题，今后看到类似的问题我们可以直接套模型，或者转化之后套模型，告别排列组合题拼运气的时代。

行测数量关系：利润问题不用愁，列表来解很轻松

在公务员考试中，利润问题是常考的题型，也是我们短期内可以提升的题型，但是令我们头疼的是利润问题里往往会出现很多的量，导致我们不容易理清各个量之间的关系，接下来带大家学习一下如何求解量比较多的利润问题。

其实遇到复杂利润问题我们只需要通过表格的方式理清各个量之间的关系，有同学可能疑惑了，这个表格到底怎么列呢?其实很简单，我们读完题干后题干中出现什么量我们就表示出什么量即可，给出数值用数值表示，没有数值直接设未知量。接下来我们通过几个例题来学习一下。

例题1:

一批商品期望获得50%的利润来定价，结果只销掉70%的商品，为尽早销售掉剩下的商品，商店决定打折出售，这样所获得的全部利润是原来所期望利润的82%，问打了几折?

A.4折 B.6折 C.7折 D.8折

【解析】答案：D。期望获得50%利润，也就是利润率是50%，设成本为x，定价为1.5x,销掉70%的商品，又提到数量，设总数为y，销掉0.7y，还剩0.3y，商店打折出售，设打折率为n，则打折后的售价为1.5xn，最后一个条件又提到利润，所以还需要表示出利润，以定价出售单件利润为1.5x-x=0.5x，则定价出售的总利润为0.5x×0.7y，打折后的单件利润为1.5xn-x，打折后总利润为(1.5xn-x)×0.3y。最终告诉我们按照所获得的全部利润是原来所期望利润的82%，期望的利润即在所有商品定价下获得的利润，也就是0.5xy。

可列表格:

最终得0.5x0.7y+(1.5xn-x)×0.3y=0.5xyx82%，等号左右两边消掉 xy，最终解得n=0.8。打八折，选D项。

例题2:

某品牌代理商2016年以80元/件的价格购进一批毛衫，以200元/件的价格卖出。2017年受市场环境影响，毛衫的进价上涨了30元，售价不变。2017年毛衫的销量比2016年提高25%，但总利润比2016年少了6万元。那么该代理商2017年销售这种毛衫共获利多少万元?

A.64    B.90    C.160    D.210

【解析】答案：B。设2016年毛衫销量为x，2017年为1.25x。

可列表格:

120x-90×1.25x=6，解得x=0.8万件。所求为90×1.25×0.8=90万元。

各位同学在今后做利润问题可以养成列表的习惯，这样解题才会不易出错。