比重问题讲解
是“量”还是“率”傻傻分不清楚
作为公务员考试中性价比较高的一类题型，资料分析在很多考生心理有着非常高的地位，其原因在于资料分析考察知识点相对比较固定，备考方向比较明确。然而，其中有两个的公式——“比重的增长量”和“平均数的增长率”很多同学容易混淆，傻傻分不清楚。今天就帮大家一起区分一下这两个公式的。
一、概念区分“量”和“率”
资料分心中按数据的呈现形式划分为“量”和“率”，“量”指有一定计量单位的绝对数，即有单位的数据；“率”是指两个相关的数在一定条件下的比值，即没有单位的数据。
“比重的增长量”是“量”，是有单位的绝对数，是通过做差得到的；
“平均数的增长率”是“率”，是无单位的相对数，是通过除法得到的：
如若A=部分的现期值，B=整体的现期值，qA=部分的增长率，qB=整体的增长率，则
二、应用区分“比重的增长量”和“平均数的增长率”
区分“比重的增长量”和“平均数的增长率”这两个公式需要结合题干和选项，进行综合判断。
(一)题干问法不同
1.“比重的增长量”的题目问法，一般有两种：
(1)与上年相比， 2012 年浙江省第三产业增加值占浙江省全年生产总值的比重上升/下降了多少？
(2)2012 年浙江省全年生产总值中浙江省第三产业增加值所占比重比2011年上升/下降了多少个百分点？
总结：不管哪种问法，题干中多会出现“xx占xx的比重” “xx中xx的比重”。
2.“平均数的增长率”的题目问法，一般为：问题：2012 年我国豆类平均产量比 2011年增长了百分之几？
总结：题干中会出现“平均产量” “单位面积产量”等表示两数之比的描述，同时问的是“增长/减少百分之几”，确定为“率”。
(二)选项书写不同
“比重的增长量”的选项书写为上升/下降多少百分点；“平均数的增长率”选项一般书写为上升/下降百分之几，如下：
【例1】截至2012年年底，全国实有企业1366.6万户，比上年年底增长9.06%，实有注册资本82.54万亿元，比上年年底增长14.24%，内资企业实有 1322.54万户，比上年年增长9.44%，实有注册资本70.71万亿元，比上年年底增长15.25%。其中私营企业1085.72万户，增长12.20%，注册资本31.1万亿元，增长20.59%，外商投资企业44.06万户，下降1.32%，注册资本11.83万亿元，增长8.52%。
问：与上年相比，2012年年底私营企业占全国实有企业总数的比重( )。
A.增加2.2个百分点 B.增加0.2个百分点
C.下降2.2个百分点 D.下降 0.2个百分点问题
【答案】A。【解析】截至2012年年底，全国实有企业 1366.6万户，比上年年底增长 9.06%，其中私营企业1085.72万户，增长 12.20%，所求为：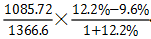
<12.2%-9.6%=2.6%，即上升不到2.6个百分点，故正确答案为A。
注意：比重的增长量=现期比重-基期比重，且结果的单位为“百分点”。
【例2】2007年全国认定登记的技术合同共计220868项，同比增长7%；总成交金额2226亿元，同比增长22.44%；平均每项技术合同成交金额突破百万元大关，达到100.78万元。
问：2007年平均每项技术合同成交金额同比增长率为多少？（ ）
A、11.15% B、14.43% C、15.44% D、35.25%
【答案】B。【解析】根据材料，平均每项技术合同成交金额=总成交金额÷技术合同项数，2007年全国认定登记的技术合同共计220868项，同比增长7%；总成交金额2226亿元，同比增长22.44%；所求为=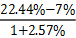
<15.44%，故正确答案为B。
注意：平均数的增长率
，且结果为“%”。
现在大家对这两个公式清晰了吗？赶紧去做题试试吧!
资料分析之分数的大小比较
各位小伙伴今天我们一起看看在公职类考试中经常出现的资料分析，资料分析的考查有两种形式：一种是考查计算能力，需要大家在短时间内估算选出答案；另一种考查比较大小能力，常见的是比较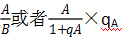
的大小。今天就带大家一起看看
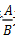这样分数的比较。
对于分数的大小比较呢我们可以按照先观察再估算的顺序来进行比较。
观察
比较大小时的观察指的就是利用分数的性质直接观察分数的大小。我们先来回顾一小分数性质：
分母相同，分子越大分数越大，比如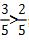
；
分子相同，分母越小分数越大，比如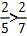
；
分子分母都不相同，分子大、分母小的分数大，比如
。
【例1】比较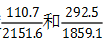
的大小。
【答案】
。【解析】在这两个分数中，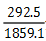
分子大，分母小，因此利用分数性质可以直接判断
。
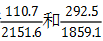估算
1.横向看倍数关系：
对于一些简单的分数利用分数的性质可以直接比较大小，也有一些分数并不具备以上三种情况，比如
，像这种情况我们可以通过横向分子与分子之间比较倍数，分母与分母之间比较倍数，然后来确定分数大小。我们一起来看一下：为了方便表述，我们把分子分母都小的分数称之为分数1，分子分母都大的分数称之为分数2。
分子比较倍数：3477是1152的3倍多；
分母比较倍数：5042是1743的2倍多。
这其实表明有分数1变成分数2分子需要乘3.X，分母需要乘2.X，说明整体乘的这个分数比1大，那么就可以判断分数1＜分数2。
在以后的判断中我们可以直接记口诀，分子的倍数大于分母的倍数，分数变大(分子分母都大的那个分数大)；分子的倍数小于分母的倍数，分数变小(分子分母都大的那个分数小)。
【例2】比较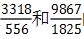
的大小。
【答案】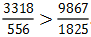
。【解析】首先我们观察是这个分数，大分子小分母没有出现在同一个分数中，这时候没有办法利用分数性质直接判断大小。接下来我们可以看一看分子与分子的倍数，分母与分母之间的倍数，然后利用口诀判断。分子与分子之间是2倍多的关系，分母与分母之间是3倍多的关系，分子的倍数小于分母的倍数，分数变小(分子分母都大的那个分数小)，这样我们就可以确定
。
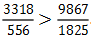2.纵向看倍数关系：
在比较分数的大小的时我们也可以将同一个分数的分子与分母进行比较，那么接下来我们结合例3给大家解释一下。
【例3】比较
的大小。
【答案】
。【解析】为了方便描述，我们把分子分母都小的这个分数叫做分数1，分子分母都大的分数叫做分数2。在分数1中，107是22的4倍多，在分数2中，172是34的5倍多，如果我们将分数1的分子分母同时缩小22倍，那分数1变为
，但分数大小不变，同样分数2的分子分母同时缩小34倍，那么分数2变为，分数大小也不变。这样原来的分数1和分数2就变为了两个分子相同的分数，利用分数性质，分母越小分数越大，因此分数1大于分数2。
如果我们是纵向找到分子与分母的倍数关系，我们可以直接将同一个分数的分子分母同时除以小数字，将两个分数转化为同分子或者是同分母，利用分数性质进行大小比较。
【例4】比较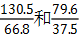
的大小
【答案】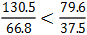
。【解析】130.5是66.8的1倍多，79.6是37.5的2倍多，分子分母同时除以小数字，那么
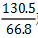就是1.X，
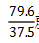就是2.X，所以
。
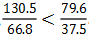以上就是我们分数比较大小的一些方法，整体来说就是先观察，利用分数性质直接判断大小；不能直接判断再估算，估算可以横向找倍数，也可以纵向找倍数：横向找倍数，利用分子的倍数大于分母的倍数，分数变大(分子分母都大的那个分数大)；分子的倍数小于分母的倍数，分数变小(分子分母都大的那个分数小)来判断分数大小。纵向找倍数，将同一个分数的分子分母同时除以小数字，将两个分数转化为同分子或者同分母，利用分数性质进行大小比较。古人云，熟能生巧，方法有了，还需要勤加练习哦。
年均增长率你会计算吗？
在行测考试里面大家都对于资料分析给予厚望，想在这部分拿到一个较高的分数，因为资料分析绝大多数的题目都是背公式再计算基本就可以拿分了，但是计算一直是大家比较头疼的部分，尤其是年均增长的计算更是繁琐，所以今天带大家来学习一下年均增长率的估算。
求年均增长率的公式是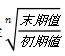
-1(n代表年份差)，但如果我们用这个公式去计算开根号n次方是不好计算的，，所以接下来给大家讲2个估算公式帮助大家解决年均增长率的计算问题。
1.当n≤5、年均增长率≤10%时，用年均增长率≈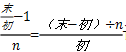
计算之后选一个略小的选项。
【例1】2019年药品流通销售收入为23303亿元，2014年为为15621亿元，问2014-2019年，我国药品流通销售收入的年均增长率约为百分之几：（ ）
A.6.7% B.7.8% C.8.3% D.9.8%
【答案】C。【解析】本题n=5，选项中的年均增长率均小于10%，所以可用第一个估算公式计算，年均增长率=(23303-15621)÷5÷15621≈9.8%，此时一定要注意要选一个略小的，故正确答案为C。
2.任何时候均可用
年均增长率≈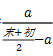
，(a代表年均增长量)，计算之后选择一个最接近的选项。为了方便大家记住这个公式我们来解释一下它的来源。我们知道求增长率可以用增长量÷(现期值-增长量)来计算，所以当我们求年均增长率时就可以将增长量换成年均增长量，而现期值就可以用(末期值+初期値)÷2来替代。
【例2】2020年中国建筑业签订合同额为595577亿元，2014年为332486亿元，问2014-2020年中国建筑业签订合同额年均增长百分之几：（ ）
A.9.3% B.10.2% C.11.1% D.12.3%
【答案】B。【解析】本题n=6，且选项中的年均增长率有的大于10%，所以无法用第一个估算公式求解，我们需要用到第二个估算公式，结合公式a=(595577-332486)÷6=43848.5，(末+初)÷2=(595577+332486)÷2=464031.5，所以年均增长率=43848.5÷(464031.5-43848.5)≈10.4%，结合选项选一个最接近的B，故正确答案为B。
对于这两个估算公式看计算量大家会发现是第一个计算量较小、容易算，所以在计算之前大家先观察选项的数据以及年份差，如果满足了n≤5、年均增长率≤10%这两个条件，大家就可以直接用第一个公式计算，如果不满足再用第二个。
