政华教育

特征数字法即为将算式中的百分数(例如增长率、比重等)转化为相同的或近似的分数，从而达到简化计算的目的。增长量的计算公式为由于资料分析中的增长率多为百分数的形式，将其转化为分数后能够进行约分处理，从而减少计算量。而题目中的增长率往往只能近似的转化为某个分数，在此过程中会产生误差，因此应用特征数字法还要注意误差的分析：即当增长率变大时，增长量也会变大，此时要选择比计算结果稍小的选项，反之，当增长率变小时，增长量也会变小，此时要选择比计算结果稍大的选项。

接下来我们就通过题目来应用一下这个方法。

例1

2017年10月份，某省实现社会消费品零售额2879.5亿元，同比增长10.1%，增速比上月回落0.1个百分点，较上年同期回落1个百分点。其中，限额以上单位消费品零售额1344.7亿元，同比增长8.4%，增速比9月份回落0.5个百分点。

问题：与2016年10月份相比，2017年10月份该省实现社会消费品零售额增长了：（）

A.254.2亿元 B.264.2亿元 C.272.6亿元 D.238.8亿元

【答案】B【解析】由材料可知，2017年10月份，某省实现社会消费品零售额2879.5亿元(即现期值)，同比增长10.1%(即增长率)，此时我们将10.1%近似的看作10%即1/10，,，则所求增长量为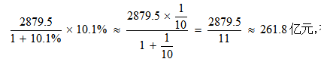在此计算过程中，我们将增长率变小，则计算结果也偏小，因此选择稍大的264.2亿元，即B项。

例2

2010年前三季度，浙江省服务业增加值为8231.91亿元，列广东(13679.63亿元)、江苏(11505.45亿元)、山东(10204.38亿元)之后，居全国第四位；同比增长11.3%，保持稳定发展。从浙江省服务业内部各行业看，交通运输、仓储和邮政业增加值为746.19亿元，同比增长12.5%；批发和零售业增加值为1818.22亿元，同比增长15.3%；住宿和餐饮业增加值为343.26亿元，同比增长12.8%；金融业增加值为1567.75亿元，同比增长12.3%；房地产业增加值为1105.73亿元，同比下降3.1%。

问题：2009年前三季度，浙江省房地产业增加值约比2010年同期( )

A.少35.37亿元 B.少33.25亿元 C.多35.37亿元 D.多33.25亿元

【答案】C【解析】由材料可知，2010年前三季度房地产业增加值为1105.73亿元(即现期值)，同比下降3.1%(即增长率)，说明房地产业增加值2009年相比2010年同期要多，排除A和B项，此时我们再将3.1%近似的看作3.3%即1/30，则所求增长量为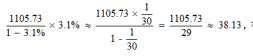在此计算过程中，我们将增长率变大，则计算结果也偏大，因此选择稍小的35.37亿元，即C项。

隔年增长率的列式及快速计算

行测资料分析中，隔年增长是一个典型的增长方式，是增长知识的延伸。在隔年增长中隔年增长率是尤为重要的存在，正确地列出式子并掌握简单的计算方法，这样才能在确保计算准确率的前提下尽可能的节省考试时间，准确完成题目。接下来就和大家分享一下如何正确地列式和又快又准地计算隔年增长率：

一、隔年增长率的公式

q=q1+q2+q1×q2（q1为现期增长率，q2为间期增长率）。

二、计算方法

q1+q2精算：q1×q2结合选项确定是否需要计算。

例1

2019年第二季度，我国挖掘机累计销售16.3万台，同比增长14.8%，上年同期增长52.7%。

问：2019年第二季度，我国挖掘机累计销量比2017年第二季度增长了百分之几？（）

A.14.8% B.52.7% C.67.5% D.75.09%

【答案】D【解析】由题干可得：2019年第二季度为现期，2017年第二季度为基期，中间隔的时期为2018年第二季度，称为间期，故求得是隔年增长率；现期增长率为14.8%，间期增长率为52.7%。则列式为：q=14.8%+52.7%+14.8%×52.7%；计算：q1+q2；精算：14.8%+52.7%=67.5%；由题目数据可知q1、q2为正值，q1×q2也必定为正值，正确答案必定大于67.5%，结合选项发现，不需要计算q1×q2的值就可以直接选择正确选项D。

以上例题结合选项不需要计算q1×q2的数值就可以选出正确选项，但是有一些题目只计算q1+q2是不能选出正确选项的，需要计算q1×q2的数值才可以，对此，给出了方法：

q1×q2的估算方法

去百分号，四舍五入取整相乘；加百分号，小数点向前移两位。

例2

2018年1-12月，全国固定资产投资(不含农户)635636亿元，比上年增长5.9%，增速与1-11月份持平，比2017年同期回落1.3个百分点。从环比速度看，12月份固定资产投资(不含农户)增长0.42%。其中，民间固定资产投资394051亿元，比上年增长8.7%，增速比上年提高2.7个百分点。

问：2018年全国固定资产投资(不含农户)比2016年增长百分之几？（）

A.13.52% B.12.31% C.9.3% D.14.6%

【答案】A【解析】由题干可得：2018年为现期，2016年为基期，2017年为间期，求的是隔年增长率；现期增长率为5.9%，由“比上年增长5.9%，比2017年同期回落1.3个百分点”得到间期增长率为5.9%+1.3%=7.2%，列式为：q=5.9%+7.2%+5.9%×7.2%；q1+q2精算：q1+q2精算：q1+q2=13.1%，q1、q2为正值，正确答案一定大于13.1%，结合选项，只能排除B、C，故需要计算q1×q2的值；q1×q2的估算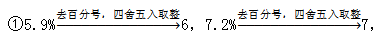：相乘：6×7=42，故可以得到q≈13.1%+0.42%=13.52%，选择A。

以上就是隔年增长率的知识，多加练习，熟能生巧，形成习惯，就可以在备考的路上越来越轻松!

资料分析中“难缠”的计算

提到行测资料分析，很多同学都有一个感受，就是这部分题目看起来很简单，但是想要做的快、做的准，却比较难。难就难在，需要计算的题目往往题量都比较大，式子比较复杂，在计算上就要花费大量的时间。那资料分析果真就只能一步步“硬”算吗？其实不见得，对于很多题目，由于数字本身具有特点，所以，我们也可以根据数字的特点，针对性地选择解题方法。今天给大家介绍一种特征数字法：

一、含义

利用百分数和分数之间的转化，将百分数近似转化为一些特定分数，从而达到简化计算的目的，该方法称为特征数字法。

举例：2176×25.2%，这个数字中25.2%实际上是非常接近于25%的，所以在计算的时候，我们完全可以把25.2%近似的看做25%，而25%=1/4，这样我们就可以大大的简化运算。42176×25.2%≈2176×（1/4）=544。

这样看起来，是不是就非常的简单。而这种将百分数近似的看做分数的方法，就是我们讲的特征数字法。关于这个方法，如果想要运用的好，就必须要知道常见的百分数和分数的转化关系，下面我们就给大家系统的梳理下：

二、常见百分数与分数的转化

上面的数字虽多，但我们发现，其实有很大一部分，是我们平时就比较熟悉的数字，如20%等，所以只要我们多做做题目，练习一下，还是可以很好的掌握这些数字的。下面我们就一起来做个题目练习一下吧：

例.7426/（1+14.1%）×14.1%=（）

A.528 B.634 C.917 D.1404

【答案】C【解析】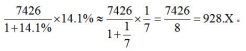选C选项。

该题目计算时，除了应用到百分数跟分数的转换外，其实我们发现，在计算中还是需要将分母上的分数，跟分子上的分数约分化简的过程，相对来说比较麻烦，这里我们有一个小技巧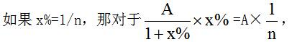，这样就可以免去化简的过程，直接得到最终的结果。

通过上面讲解，相信各位考生对特征数字法已经有所熟悉。这部分内容如果掌握得当，对做题来说是很有帮助的，可以在计算中，免去一步一步纷繁复杂的计算过程。各位考生一定要多加练习，熟练掌握这种方法。

巧用放缩规避易错点

在行测资料分析题目的计算过程之中，我们常常采用的两种方法是特征数字法和有效数字法。特征数字法是将百分数转化为简单分数，从而达到简化计算的目的的一种计算方法；有效数字法是通过不同列式对应的取舍原则，结合选项从而快速确定答案的一种计算方法。

相较于特征数字法，由于简单分数的个数有限，且误差不易判断大小，所以并不是所有百分数都能找到其接近的简单分数并估算出合适结果，而有效数字法则并没有太多的限制。在这种情况下，很多同学就偏爱于有效数字法，而冷落了特征数字法。但存在即合理，特征数字法也有其独特的魅力，那就是作为一种估算的方法，计算时其放大或缩小的方向往往是固定的，而有效数字法计算时由于可能存在分子“一进一舍”、分母“四舍五入”等原因，其放缩方向难以把握。基于此因，一部分题目在计算无误的情况下，采用有效数字法就有可能错选答案。而利用特征数字法放缩方向确定的特点，就可以规避这样的问题，我们来看一道题目：

例.

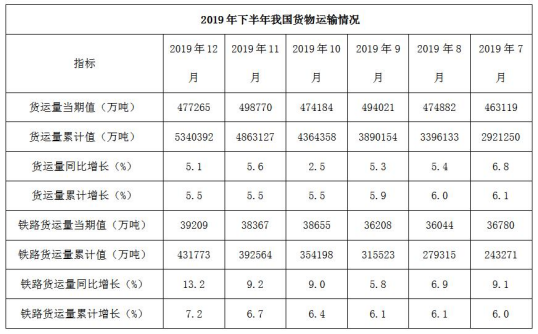
问题：2019年7月，我国铁路货运量同比增长了( )

A.3041万吨 B.3068万吨 C.3092万吨 D.3115万吨

【答案】B【解析】这道题求的是2019年7月我国铁路货运量的增长情况，结合选项中的单位“万吨”，因此求的是铁路货运量的增长量。观察表格数据，发现可以找到2019年7月我国铁路货运量的当期值36780万吨，也能找到其同比增速9.1%。利用增长的公式，可知其增长量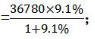此时若使用有效数字法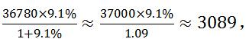，与3089最接近的是3092，因此错选C；

若使用特征数字法，9.1%可近似看做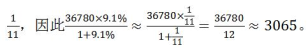

我们知道是将增长率q变小了，因此（A×q）/（1+q）这种式子其结果也变小了，我们需要找一个比结果3065大的数字，最接近的是3068，选B。

【总结】无论是特征数字法还是有效数字法，其本质都是一种估算方法。既然是估算方法，就有可能产生误差。两种方法比较起来，特征数字法对于结果是放大还是缩小往往容易判断(总结于下文)，而有效数字法中“一进一舍”情况较为常见，其放缩特性并不好判断。因此，可能会因误差错选答案。

通过这道题目，我们发现，利用特征数字法的“放缩”特性去规避错误的题目有如下特征：

1.选项差距较小。这点尤为重要，如果选项差距大时，无论特征数字法还是有效数字法，选择最接近的选项即可，也就不会出现有效数字法计算无误而选错答案的问题了。

2.有较为常见的“特征数字”。也就是常见的能够化为简单分数的百分数。

同时，在判断放缩的过程中，要能够对特征数字法的放缩特性熟记于心：

1.A×q的式子中，若q变大，结果变大，选一个比结果小的数字，反之选比结果大的数字；

2.A/q的式子中，若q变大，结果变小，选一个比结果大的数字，反之选比结果小的数字；

3.A×（q/1+q）的式子中，若q变大，结果变大，选一个比结果小的数字，反之选比结果大的数字。

通过以上所述我们不难发现，在计算时最好不要一种计算方法“一条道走到黑”，政华教育提醒大家，要及时根据题目特点及选项差距调整计算方法，必要时考虑放缩，从而达到规避错误的目的。