行测资料分析技巧

行测资料分析十字交叉法巧解“混合比值”问题

行测资料分析中有一类题目，同学们在遇到的时候都会很头疼，那就是混合比值问题。对于这样的题目，同学们可以设未知数列方程求解，但显然解题时间相应的会比较长，那有没有更好的方法解决这类问题呢？接下来带领大家学习一类比较简单的解法——十字交叉法。

什么是混合比值问题

1.资料分析中的比值

在资料分析中，常考察等这类比值的混合。

2.比值如何混合

以平均分为例，全班女生的平均分=女生的总成绩/全班女生人数，全班男生的=男生的总成绩/全班男生人数，全班的平均分=全班的总成绩/全班人数。可以看到：全班平均分的分子为女生和男生分子之和，分母也为女生和男生分母之和。

如果把全班的平均分称为整体比值，女生的平均分和男生的平均分称为部分比值。整体比值的分子为两个部分比值的分子之和，分母为两个部分比值的分母之和。像存在以上这种加和关系的题目，就属于混合比值问题，可以应用十字交叉法来求解。

如何应用十字交叉法

应用十字交叉法需要记住三点规律：

1.整体比值介于部分比值之间。

2.整体比值更靠近分母较大的部分比值。

3.比值交叉作差后的结果之比为分母之比。

下面通过例题进行讲解说明。

例1：2013年全国中高等学校在校博士生为283810人，其中少数民族学生所占的比重为5.23%；在校硕士生为1436008人，其中少数民族学生所占比重为5.89%。

问题：2013年全国中高等学校研究生中，少数民族研究生所占比重约为：（   ）

A.5.23%       B.5.38%         C.5.56%        D.5.78%

【答案】D【解析】这道题研究的是比重。由材料可知，博士中少数民族占比为5.23%，硕士中少数民族占比为5.89%，所求为研究生中少数民族占比，为三个比值，且这三个比值符合分母间、分子间的加和关系，即：研究生=博士生+硕士生，研究生少数民族人数=博士生少数民族人数+硕士生少数民族人数，故可用十字交叉法求解。所求即为整体比值，由第一点规律可知整体比值介于部分比值之间，即所求介于5.23%和5.89%之间，排除A项。进一步应用第二点规律：整体比值更靠近分母较大的部分比值，该题两个部分比值分母分别为在校博士生数量和在校硕士生数量，由材料可知：2013年全国中高等学校在校博士生为283810人，在校硕士生为1436008人，283810<1436008，故所求更靠近硕士中少数民族的占比(5.89%)，即大于(5.23%+5.89%)÷2=5.56%，选择D项。

例2：2017年9月，广东省进出口总额同比增长8.1%，其中，进口额同比增长14.2%，出口额同比增长4.5%。

问题：2016年9月，广东省出口额约是进口额的多少倍（   ）？

A.1.2        B.1.5         C.1.7         D.2.4

【答案】C【解析】所求是几倍=2016年9月广东出口额/2016年9月广东进口额，但由于材料中仅有2017年9月进口额和出口额的增长率，无法直接求出2016年9月进口额和出口额进行求解。已知增长率（增长量/基期值）为比值，2017年9月进出口总额增长率、进口增长率和出口增长率三个比值的分子分母间也存在加和关系，且所求为进口额和出口额两个部分增长率的分母之比，故可以用十字交叉法的第三点规律求解，即比值交叉作差后的结果之比为分母之比。由材料可知，2017年9月广东省进出口总额的增长率为8.1%，其中进口额增长率为14.2%，出口额增长率为4.5%，交叉作差结果如下：

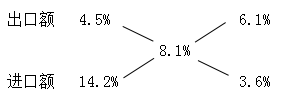
由十字交叉法的模型可得，所求为：2016年9月出口额/2016年9月进口额=6.1%/3.6%≈1.69倍，选择C。

相信通过以上两道题目，大家已经对十字交叉法解决混合比值问题有所了解，但熟练地应用建立在大量的练习基础上，希望各位考生备考期间多多做题，提升这类问题的解题能力。

行测资料分析：深入辨析平均数增长量和增长率

在行测考试中，资料分析主要考查的是对统计材料的理解、把握、查找比较的能力，而资料分析近些年来，对于平均数相关知识点的考察越发的重视，但是由于而均数本身难度比较大，公式以及相关计算比较复杂，成为许多考生比较头疼的问题。其实对于平均数而言，也有许多小的技巧，只要掌握了计算方法、理解了题干的本质，就可以达到迅速解题的目的。今天带大家一起来学习资料分析的一个重要考点——平均数的增长量和增长率。

基本概念

基本概念：平均数增长量是指现期平均数相对于基期平均数所增长的量。

平均数增长率则指的是现期平均数相对于基期平均数所增长的百分比。

区别：通过概念我们可以了解到，由于平均数本身是一个带单位的具体的量，因此平均数的增长量也是一个量且单位不发生变化，而平均数的增长率则是具体量的增长率，是一个百分数的形式。

基本公式

解题及计算方法

（1)平均数增长量。

例1：

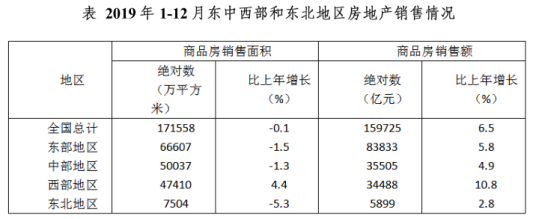
问题：与2018年相比，2019年全国商品房销售均价约：（   ）

A.增长580元

B.增长710元

C.下降580元

D.下降710元

【答案】A【解析】首先确定考点，全国商品房销售均价为平均数，出现了选项为增长或者下降且带单位，因此所求为平均数的增长量，而所求为全国商品房销售均价，销售额为总量，面积为份数。全国商品房销售面积和销售额分别为171558万平方米和159725亿元，同比分别增长-0.1%和6.5%，因此列式为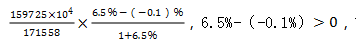故排除C，D选项。由于选项数量级相同，我们在计算时只需要计算结果的有效数字即可，6.5%-(-0.1%)=6.6%，而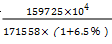略小于1，因此6.6%乘一个略小于1的数，一定变小，因此其有效数字应比6.6%的有效数字略小，选则稍小的A项。

小结：求平均数的增长量时，我们可类比比重的增长量计算方式，通过计算结果的有效数字结合选项排除错误答案来选择正确答案。

（2)平均数增长率。

例2：

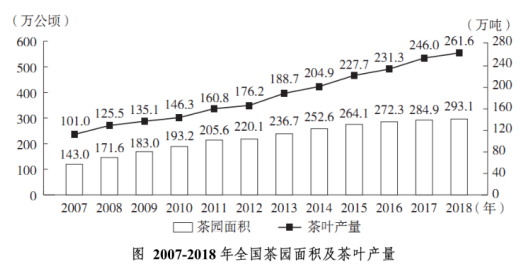
问题：2007-2018年，全国茶园面积首次超过200万公顷的年份，当年茶园单位面积茶叶产量比上年：（   ）

A.增加了不到10%

B.增加了10%以上

C.下降了不到10%

D.下降了10%以上

【答案】A【解析】由图形材料可知，2007-2018年全国茶园面积首次超过200万公顷的是2011年，当年茶叶产量为160.8万吨，茶园面积为205.6万公顷，则茶园单位面积茶叶产量为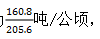2010年茶园单位面积茶叶产量为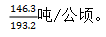所求为园单位面积茶叶产量比上年增加的百分数，为平均数的增长率，由于题干中未出现增长率，因此需用原始公式求解，代入数据列式为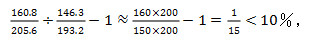故选A。

小结：

（1)求平均数的增长率时，如果选项是精确的数值且给定了总量和份数的增长率，可直接套公式若选项为精确数没有给出总量和份数的增长率，而是分别给出了现期和基期的总量和份数，则要套用原始公式求解。

（2)求平均数的增长率时，若选项为一个范围且没有给出总量和份数的增长率，而是分别给出了现期和基期的总量和份数时，可采用估算的方式，分别计算总量和份数的增长率，再代入原始公式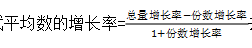去计算。

以上是平均数增长量和增长率相关的公式以及解题技巧。希望对大家的备考有所帮助，也希望大家在今后的练习中灵活应用，提高做题速度以及正确率。

“时间段”原来喜欢这样挖陷阱

每次资料分析做错了，在看过答案之后，小伙伴们都有这样一个想法：这道题不难，我会，是粗心大意导致做错了。结果下次遇到类似的题目还是会出错，这就要引起重视了，因为你步入了题目陷阱却还浑然不知。接下来就带大家见见题目中的“时间段”都喜欢挖哪些陷阱，助力大家有效避坑。

例1：

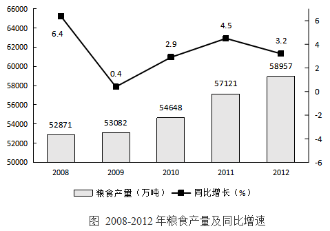
问题：根据所给资料，下列说法正确的是：（   ）

A.从2008~2012年，粮食产量增长率逐年提高

B.若按照2012年的同比增速，2013年粮食产量将超过6.5亿吨

C.2013年粮食产量增长2000多万吨

D.2007年粮食产量接近5亿吨

我们来分析一下例1：

可以看出题目选项主要涉及到的都是时间段的端点，那么端点处都喜欢考察哪些考点呢？我们一个一个来看：

B项，所求为现期值，虽然2013年的值图中并没有提到，但若已知2013的同比增速，那么2013的值便可求；若这个选项改成“B.2013年粮食产量将超过6.5亿吨”，此时并不知道2013年的增长率，则这个时候2013年的值就无法求出了。

C项，所求为2013年的增长量，而图中已知的只有2012年的值，并不清楚2013年的同比增长率或者2013年的值，因此条件缺失，无法求出。但若将这个选项改成“C.若2013年同比增速为5%，2013年粮食产量增长2000多万吨”此时2013的增长量便可求。

D项，所求为基期值，虽然2007年的值图中并没有提到，但已知2008年的值和增长率，基期就可求。

【答案】D【解析】A项，根据折线图观察增长率，并非逐年提高，错误；B项，想求2013年(现期)的值，已知2012年的值和2013年的增长率，则所求为58957×(1+3.2%)≈59000万吨=5.9亿吨<6.5亿吨，错误；C项，材料已知2012年的值，无法得知2013年及以后的数据，无法判断；D项，材料已知2008年的值和其增长率，可求2007年的值，为52871÷(1+6.4%)≈52871÷1.06=49XXX万吨=4.9XX亿吨，正确。综上，本题应该选择D选项。

现期值、基期值、增长量都是端点会考察到的计算，那关于端点时间的值究竟何时可求，何时不可求，是同学们经常容易搞混的地方，也是题目爱出小陷阱的地方，我们需要注意！举个例子，我们来看下面这道题。

例2：

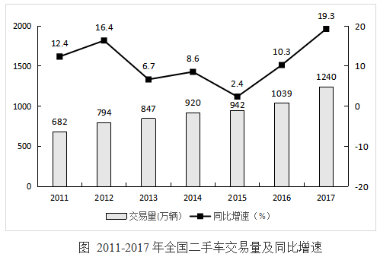
问题：2011-2017年，全国二手车交易量同比增量低于80万辆的年份有几个（  ）？

A.4       B.3         C.7         D.5

我们来分析一下例2：

这道题大家可能比较容易错选为B项，因为忽略了其端点年份2011年。虽然材料中没有给出2010年的值，但通过2011年的值及其增长率，同样可以求出2011年的同比增量，这是需要同学们关注到的小陷阱。

【答案】A【解析】由图可知，2011年的同比增量为2013年为847-794=5X万辆，2014年为920-847=7X万辆，2015年为942-920=2X万辆，2016年为1039-942=9X万辆，2017年为1240-1039=2XX万辆。比较可知，同比增量低于80万辆的有2011年、2013-2015年，共4年，本题应该选择A选项。

通过以上两道题，相信大家也看到了对于“时间段”来说，小陷阱容易出现在端点的位置，因此对于端点我们需要格外注意。给大家总结了以下两点：

1.若给了端点时期的值及增长率，可求基期可求增长量，但不可求现期(若已知现期的增长率，则可求)。

2.在求值或计数时，时间端点勿要忘。

“三步走”解决比重变化量问题

资料分析是行测试卷中备考难度相对适中的部分，但比重增长量的计算是考试的难点之一，这类题目公式复杂，需要查找多个数据代入公式进行求解，并且直接利用基本公式求解，计算量相对来说比较大，但是这种题目虽然看起来列式复杂，计算的时候却可以通过简单计算配合选项的设置比较轻松的解决这类问题，今天就带大家来学习一下如何解决比重增长量问题。

第一步：先根据部分增长率与整体增长率的大小关系判断比重上升还是下降，排除部分选项。

部分增长率>整体增长率，现期比重上升；

部分增长率<整体增长率，现期比重下降；

部分增长率=整体增长率，现期比重不变。

例题：2015年一季度，某省省级及以上园区(以下简称园区)实现主营业务收入7062.85亿元，同比增长11%。实现主导产业主营业务收入4369.54亿元，同比增长10.4%。一季度，全省园区共实现利润279.54亿元，同比增长11.1%。上缴税金223.87亿元，同比增长14.1%。

问题：2015年一季度，该省园区企业上缴税金占主营业务收入的比重比上年同期：（   ）

A.上升了0.1个百分点            B.上升了3.1个百分点

C.下降了0.1个百分点            D.下降了3.1个百分点

【答案】A【解析】由材料可知，2015年园区企业上缴税金同比增长14.1%，高于主营业务收入的11%，14.1%>11%，故比重上升了，排除C、D选项。

第二步：比重增长量的绝对值小于部分增长率和整体增长率差的绝对值。

例1：2015年一季度，某省省级及以上园区(以下简称园区)实现主营业务收入7062.85亿元，同比增长11%。实现主导产业主营业务收入4369.54亿元，同比增长10.4%。一季度，全省园区共实现利润279.54亿元，同比增长11.1%。上缴税金223.87亿元，同比增长14.1%。

问题：2015年一季度，该省园区企业上缴税金占主营业务收入的比重比上年同期：（   ）

A.上升了0.1个百分点           B.上升了3.1个百分点

C.下降了0.1个百分点           D.下降了3.1个百分点

【答案】【解析】由材料可知，2015年园区企业上缴税金同比增长14.1%，高于主营业务收入的11%，故上升，14.1%-11%=3.1%，即3.1个百分点，选择小于3.1个百分点的，故选择A选项。

第三步：若选项存在多个小于，那么估算(现期部分/现期整体)×[(部分增长率-整体增长率)/(1+部分增长率)]。

例2：2017年全国海洋生产总值77611亿元，比上年增长6.9%，海洋生产总值占国内生产总值的9.4%。

2017年，J省海洋生产总值为7217亿元，比上年增长9.2%，海洋生产总值占地区生产总值的8.4%，2017年，全省沿海沿江港口完成货物吞吐量20.4亿吨，同比增长8.3%；集装箱吞吐量1698.8万标箱，同比增长5.5%。

问题：2017年J省海洋生产总值占全国的比重比上年：（   ）

A.上升了约0.2个百分点             B.上升了约2个百分点

C.下降了约0.2个百分点             D.下降了约2个百分点

【答案】A【解析】由材料可知，2017年全国海洋生产总值77611亿元，比上年增长6.9%，J省海洋生产总值为7217亿元，比上年增长9.2%，9.2%>6.9%故比重上升，排除C、D选项，9.2%-6.9%=2.3%。A、B选项均小于2.3个百分点，故估算，列式为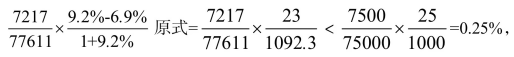上升了不到0.25个百分点。只有A项符合。故本题选A。

相信大家通过上述量道题目，能对比重的增长量问题有所了解，建议大家在备考期间需多多练习真正将计算方式掌握好，真正做到熟练掌握这类问题，希望对于大家的备考能有所帮助。