行测资料分析如何快速解决复杂运算技巧

行测资料分析：复杂的乘除运算也能很简单

行测考试中资料分析部分数据大多不整且数位较多，当遇到乘除混合运算时，很多同学会感到计算起来无从下手，不知道该如何取舍，怎样取舍才能既算得快，又能保证准确度。接下来政华公考为大家介绍如何快速解决乘除混合运算。

整体来说，乘除混合运算可通过保留适当有效数字约分计算、利用特征数字计算等方式快速求解。

一、根据数据特点，保留适当有效数字约分后，简单计算得出答案

例1：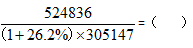

A.1.36         B.1.24        C.1.07           D.0.92

【答案】A【解析】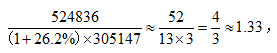选择最接近的A项。

二、根据数据特点，约分后直接与选项比大小得出答案

例2：

A.20%       B.32%       C.47%         D.58%

【答案】D【解析】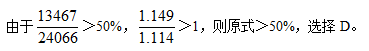对于列式类型为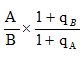的式子，即利用现期值和增长率求解基期倍数、基期比重或基期平均数时，可根据数据特征先约分判断与选项比大小得出答案。

第一、二点需要大家通过观察分子、分母的数据特点进行约分处理，但不是所有式子都能通过约分进行估算的，约分这步操作需要大家通过不断地练习提升数据的敏感，可不是一蹴而就的。

三、数据有特征时，通过转化成易于计算的分数，快速估算结果

例3：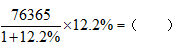

A.8304         B.8533         C.8718           D.8902

【答案】A【解析】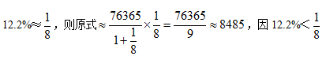，则原式<8485，选择略小的A项。对于列式类型为转化成分数再进行简便运算。当结合选项无法确定答案时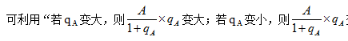，变小”判断计算结果与实际结果之间的大小关系，得出答案。

各位考生，以上就是乘除混合运算的一些技巧。各位考生自己可以再多找一些试题去练习一下。多算、多练，把方法用熟了，才能提升大家在资料分析中的计算速度和准确率。

容斥极值思想在行测资料分析中的应用

近年来行测考试不断推陈出新，对比以往的题目而言，对于知识点的考察不再仅仅局限于表面上的公式的基本运用，在当今的考试中更多地测查考生的理解与灵活运用能力，现如今的考点也已经从基本公式向着更加多元的方向去延伸，今天政华公考给大家带来的是容斥极值思想在资料分析中的具体应用。

容斥极值公式

(A∩B)最小值=A+B-I

容斥极值问题的题型特征

1.区域出现重叠。

2.出现“最少”、“至少”等字眼。

经典例题

例1：某市统计局在针对噪音扰民的一次调查中，当问及是否支持广场舞活动时，12.8%的受访市民表示无所谓或者不知道，12.0%的受访者回答表示反对，其他为支持者。在支持的市民中，当被问及支持的主要原因(多选)时，不同年龄段受访者的回答如下表所示。

此次调查中，在支持广场舞等活动的受访青年市民中，同时选择“中老年人的正常锻炼娱乐活动”和“有利于中老年人扩大社交、排解孤独”的至少有：（   ）

A.64.7%        B.35.3%       C.30.7%          D.28.6%

【答案】C【解析】通过表格可知，在支持广场舞等活动的受访青年市民中，选择“中老年人的正常锻炼娱乐活动”的比例为66%，选择“有利于中老年人扩大社交、排解孤独”的比例为64.7%，而66%+64.7%>100%，说明两者之间出现了重叠；问题中体现“至少”，故此题可以考虑容斥极值的应用。选择“中老年人的正常锻炼娱乐活动”的比例记为“A”，选择“有利于中老年人扩大社交、排解孤独”的比例记为“B”，根据容斥极值问题的基本公式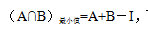可得同时选择“中老年人的正常锻炼娱乐活动”和“有利于中老年人扩大社交、排解孤独”的至少有：66%+64.7%-100%=30.7%，故答案为C。

例2：2020年，江苏省经济运行恢复向好，高质量发展有力推进，实现GDP达10.27万亿元，增速比全国平均高出1.4个百分点。需求结构持续优化。高技术产业投资增长8.4%，高技术服务业投资增长29.9%，机电设备、高新技术产品出口占全省出口总额的比重分别为66.8%和37.2%。

2020年江苏高新技术产品出口额中机电设备出口额的比重至少为：（   ）

A.3.8%        B.10.8%       C.26.3%         D.33.5%

【答案】B【解析】由问题“2020年江苏高新技术产品出口额中机电设备出口额”可知，“高新技术出口额”和“机电设备出口额”之间存在重叠；且问题中体现“至少”，故此题考虑容斥极值的应用。此题中，部分为“机电设备出口额”，记为“A”；整体为“高新技术产品出口额”，记为“B”。根据“机电设备、高新技术产品出口占全省出口总额的比重分别为66.8%和37.2%”以及容斥极值问题的公式(A∩B)最小值=A+B-I可得，2020年江苏高新技术产品出口额中机电设备出口额的比重至少为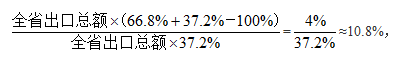：故答案为B。

正所谓学则变，变则通，政华公考希望大家在资料分析中碰到容斥极值问题能够做到识特征，巧应对，以上就是今天为大家带来的关于容斥极值思想在资料分析中的实际应用。

行测资料分析长题干读不懂怎么办？

在行测考试中，资料分析是拿分的重点，经过学习之后，会发现有时候资料分析不难，只要记住公式多练习计算，大部分题目就没问题。但也有部分题目挺难，甚至读不懂。这一类题目大部分是题干长并且较为复杂，但是考点往往难度不大，弃之可惜。那么，遇到这类题干我们如何快速解读呢？较为复杂的长题干常出现的一般有两类：前提条件型题干、假设型题干。对于不同的题干类型，我们要用不同的办法攻克，从而解决这一类难题。

含有前提条件的题干

这类题型的题干前半部分是让考生根据要求确定指标，后半部分考察该指标的一些基本考点。因此，题干后半部分经常会出现“其”这个字眼用来代指我们通过前提条件找到的指标。一般我们可以分阶段解读题干，先根据题目前半段要求，找到符合条件的指标。然后再对该指标对应的数据按照题目后面的要求进行计算或比较。

例1：

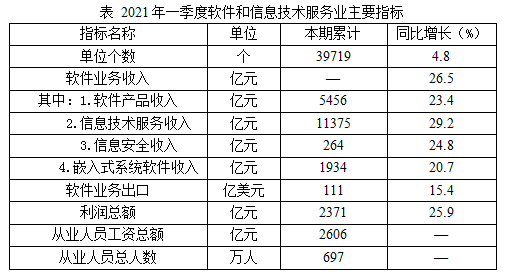
问题：2021年一季度，软件和信息技术服务业软件业务收入中，占比较上年同期上升的收入类别，其收入所占的比重约：（   ）

A.28.8%       B.59.8%    C.1.4%            D.10.2%

【答案】B【解析】题干中前半部分“软件和信息技术服务业软件业务收入中，占比较上年同期上升的收入类别”为前提条件，第一步需要找到比重上升的这一类别；可以通过判断比重变化的方法寻找。由表可知，2021年一季度，软件和信息技术服务业软件业务收入中，只有信息技术服务收入同比增速(29.2%)>软件业务收入同比增速(26.5%)，故2021年一季度，软件和信息技术服务业软件业务收入中，符合前提条件的收入类别为“信息技术服务收入”，题干中后半段“其收入所占的比重约？”目的是让我们求解出此类收入占比，利用现期比重公式直接求解，所求为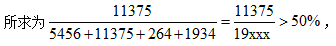选择B。

含有假设条件的题干

含有假设条件的题干，一般先给出假设条件，然后让考生依据材料数据结合假设条件，对问题进行求解。题干一般会有这样的特征：(1)开头经常会出现“如果”、“假若”、“假设”、“若”等字眼。(2)后半段题干有时会用连接词连接(例如：“如果……那么……”、“假设……则……”)，或用逗号隔开(例如：“若……，……”)。这样的题目题干往往较长，很多考生做这类题目读完之后非常焦虑，在考场上紧张状态下，更加崩溃。

拿到这类题目，我们可以大概扫一眼前面的假设条件，但是不要过度关注。重点应该放在题干后半段题干，以连接词“则”、“那么”或者标点“，”为分界，重点理解后面的要求，确定考点后，根据材料数据以及题干所给的前提条件进行求解。

例2：2016年前三季度，湖北省固定资产投资累计完成21133.23亿元，增长13.4%，环比提高0.1个百分点，比二季度投资增速高0.1个百分点，比上年同期增速低2.8个百分点。

问题：若2015年第四季度湖北省固定资产投资占全年的比重为28.6%，则2015年湖北省固定资产投资约为多少亿元？（   ）

A.29598       B.26101      C.23581      D.18187

【答案】B【解析】题干开头出现“若”这一字眼，可判断为假设型题干，可以简单理解，重点读“则”后面的要求：“则2015年湖北省固定资产投资约为多少亿元”题干时间与材料时间不同，让我们求解2015年(基期)的固定资产投资。回顾材料发现并没有给出2016年全年数据，只给出前三季度数据，这时需要结合假设条件“若2015年第四季度湖北省固定资产投资占全年的比重为28.6%”求解，根据假设条件可知2015年前三季度占全年比重为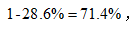且由第一段可知，2016年前三季度，湖北省固定资产投资累计完成21133.23亿元，增长13.4%，则2015年前三季度，湖北省固定资产投资累计完成因此所求为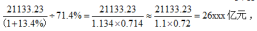选B项。

通过上面两道例题政华公考给大家介绍了常见的长题干解读方法，需要大家将解题方法运用到实际题目中，精选题目进行针对性练习，最终攻克长题干题目。

行测资料分析：“十字交叉法”巧解比值混合问题

资料分析是行测考试中的易得分题型，但其中的比值混合问题却让许多考生在此类题型中栽了跟头，纵然利用常考公式能解出答案，但往往列式复杂又难算，从而耗费大量时间。因此，今天政华公考就给大家介绍一种快速解决比值混合问题的方法——十字交叉法。

基本概念

比值混合：概念或时间上有加和关系的两数比值的求解。

比值：一般求增长率、比重或者平均数。

混合：概念加和关系，如：进出口总额=进口总额+出口总额；时间加和关系，如：上半年=一季度+二季度。

常用结论及例题展示

结论一：整体比值介于部分比值之间。

示例：假设有两种浓度分别为30%和50%的NaCl溶液A和B，若将两种溶液混合得到溶液C，则C的浓度一定处在30%~50%之间。

例1：2014年全国社会物流总额213.5万亿元，同比增长7.9%，其中上半年101.5万亿元，同比增长8.7%。

问题：2014年下半年社会物流总额同比增长（   ）。

A.7.2%        B.8.0%        C.8.6%      D.9.3%

【答案】A【解析】由题目可知，2014年全国社会物流总额为2014年上半年社会物流总额与下半年社会物流总额之和，所求增长率又是比值的形式，因此根据十字交叉法结论一可知，2014年全国社会物流总额的增长率(7.9%)应介于2014年上半年社会物流总额增长率(8.7%)与下半年社会物流总额增长率之间，7.9%<8.7%，故2014年下半年社会物流总额的增长率小于7.9%，选择A选项。

结论二：整体比值偏向于分母更大的一方。

示例：假设有两种浓度分别为30%和50%的NaCl2溶液A和B，若将两种溶液按1：1混合得到溶液C，则C的浓度为40%；若所加溶液质量A>B，由于A的浓度较低，故C的浓度应当处于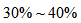之间；若所加溶液质量A<B，由于B的浓度较高，故C的浓度应当处于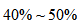之间。

例2：2015年1-4月累计城镇消费品零售额80056亿元，同比增长10.2%；乡村消费品零售额13046亿元，增长11.5%。

问题：2015年1-4月累计社会消费品零售总额同比增长（   ）。

A.9.9%        B.10.4%        C.10.9%        D.11.6%

【答案】B【解析】根据结论一，2015年1-4月累计社会消费品零售总额的增长率应介于城镇消费品零售额的增长率(10.2%)和乡村消费品的零售额增长率(11.5%)之间，故排除A、D项。由结论二可知，由于城镇消费品零售额的基期值更大，社会消费品零售总额增长率应当偏向于城镇消费品零售额增长率，范围缩小为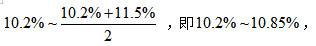即选择B项。

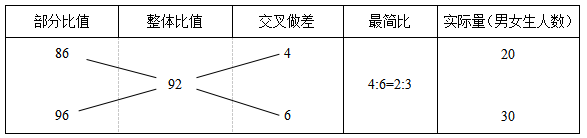
结论三：交叉作差所得最简比为分母之比。

示例：假设某次考试男女生的平均分分别为86分和96分，已知全班平均分为92分，则男女生人数之比为：（   ）

例3：2011年8月新疆全区规模以上工业实现增加值235.25亿元，比上年同期增长10.6%，其中轻工业实现增长15.4%，重工业实现增长10.2%。

问题：2010年8月新疆全区规模以上重工业增加值是轻工业增加值的多少倍？（   ）

A.8.3           B.12      C.23       D.1.3

【答案】B【解析】

2010年8月规模以上重工业增加值是轻工业增加值的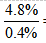12倍，选择B选项。

相信通过上述的例题展示大家已经对“十字交叉法”巧解混合比值问题有更加深刻的认识，政华公考建议大家备考期间多加练习，以便从容面对此类题目！