政华教育

古典概率又称等可能事件的概率，具有两个特征：“有限性”和“等可能性”。“有限性”强调基本事件是有限的、可数的；“等可能性”强调每一个基本事件发生的可能性是相等的。在古典概率中，A事件发生的概率用P(A)来表示，即要求概率是多少，只需要确定“总事件包含的等可能样本数”和“A事件包含的等可能样本数”，求样本数我们常用的方法是枚举法和排列组合。接下来政华公考通过几道例题来讲解。

经典例题

例1：某次知识竞赛试卷包括3道每题10分的甲类题，2道每题20分的乙类题以及1道30分的丙类题。参赛者赵某随机选择其中的部分试题作答并全部答对，其最终得分为70分。问赵某未选择丙类题的概率为多少？（）

【答案】D【解析】根据题干，试卷中题目数是可数、有限的；赵某随机选择题目，每个题目被选择的可能性相等，所求为古典概率。A事件为赵某未选择丙类题，总事件为最终得分为70分。根据题意，最终得分70分，有以下三种分类：

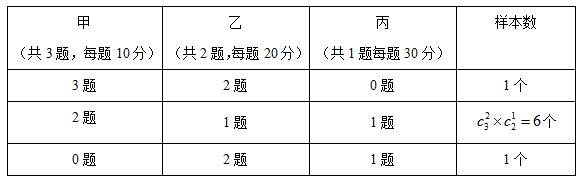
由上表可知最终得分70分的总样本数为1+6+1=8个，未选择丙类题目样本数为1个，故所求概率为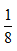。故本题选D。

例2：已知一个箱子中装有12件产品，其中2件次品。若从箱子中随机抽取2件产品进行检验，则恰好抽取到1件次品的概率是：（）

【答案】B【解析】根据题干，产品数是可数、有限的；从箱子中随机抽取的每一个产品的可能性相等，所求为古典概率。A事件为抽取的2件产品中恰好有1件次品；总事件为从12件产品中任意抽取2件产品。已知12件产品中有2件次品，10件合格品，A事件包含的等可能样本数为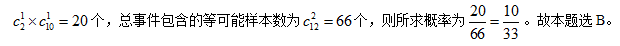

通过上面两个例题可以看出，古典概率的破题之法，一是要掌握好公式确定并计算出A事件和总事件包含的等可能样本数；二是对枚举法和排列组合知识点也要熟练掌握。相信大家掌握了破题之法后，经过不断的练习，古典概率问题能够快速破解。

敲开行测方程法的那块砖——等量关系

行测考试的难度是不容小觑的，而在种种的题型中，数量关系成为很多考生的“心病”。今天，政华公考就带大家来了解一种治疗这种“心病”的良药——方程法。方程法解数学应用题基本贯穿了我们从小到大的数学生涯，而想要用方程解题，寻找等量关系是重中之重的一步。找等量关系可以分成几种不同的情况：

一、根据题干的描述找等量关系

例1：甲乙两个单位的人数相同，甲单位党员人数占总人数的20%，乙单位的党员人数占总人数的25%，如果乙单位的20名党员与甲单位的20名群众互换单位则两个单位的党员占比相同。问两个单位共有党员多少人？（）

A.256 B.288 C.324 D.360

【答案】D【解析】设甲乙两个单位总人数皆为x，则甲单位党员人数为20%x，乙单位党员人数为25%x。根据“乙单位的20名党员与甲单位的20名群众互换单位则两个单位的党员占比相同”，交换完毕后两个单位的总人数并不发生变化，占比相同代表党员人数相同，可以列出20%x+20=25%x-20，解得x=800，则甲单位党员人数为160，乙单位的党员人数为200，总党员人数为360，故选D。

其实根据题目中的一些描述即可找到等量关系，比较常见的描述有：……与……相同(等)、……与……共、……比……多(少)、……是……倍数(百分之几)等等，总结来说就是能说明数量之间关系的语句。找到等量关系后，按部就班设未知数解方程即可解题了。

二、题目中描述了不同方案，根据不同方案中的不变量找等量关系

例2：某企业员工组织周末自驾游。集合后发现，每辆小车坐5个人，则空出4个座位；如果每辆小车少坐一个人，则有8人没有上车。那么自驾游小车共有多少辆？（）

A.9 B.10 C.11 D.12

【答案】D【解析】题目中两种乘车方案中，总人数不变，可以根据两种方案的总人数相等列方程。设：共有x辆车。5x-4=4x+8，解得x=12，则共有12辆小车，故选D。

类似于这类题目，给出不同的方案，我们就可以找到不同方案中的不变量。根据不同方案中该不变量相等这个等量关系列方程解题。

三、根据常见公式找等量关系

例3：小李四年前投资的一套商品房价格上涨了50%，由于担心房价下跌，她将该商品房按市场价的9折出售，扣除成交价5%的相关交易费用后，比买进的时候赚了56.5万元。那么，小李买进该商品房时花了多少万元？（）

A.200 B.250 C.300 D.350

【答案】A【解析】设：买房时的成本为x万元。根据总收入-总成本=利润的公式，可以列出1.5x×90%×(1-5%)-x=56.5，解得x=200，故选A。

这道题目就是根据利润问题中的基本公式找到的等量关系列出方程解决的问题。类似可能涉及到的题型还有：工程问题，行程问题，浓度问题等等。需要大家好好记住相关题型的公式，对于我们解题十分有帮助。

政华公考希望大家在行测学习过程中自己多加练习，因为数学题目与其他的各种学习一样，都需要量变积累到质变的过程。想要有提升必须付出相应的努力。希望大家达成所愿，成就美好人生。

解决行测排列组合问题的三大方法

在行测数量关系中，排列组合问题因其灵活多变，往往给同学们带来很大的困扰。在排列组合中有部分题目条件较多，大家在处理的时候就需要有一定的章程，才能快速梳理出解题的思路，这就需要我们借助一定的方法。接下来，政华公考就带大家一起学习下行测考试中常用的解决排列组合问题的三大方法，大家熟练掌握这些方法后，解决排列组合问题时便能游刃有余。

优限法

题型特征：题干中有绝对限制条件的元素或者位置。

优限法的使用：优先考虑有绝对限制条件的元素或位置，再考虑其他的元素或位置。

例1：一次会议某单位邀请了10名专家，该单位预定了10个房间，其中一层5间、二层5间。已知邀请专家中4人要求住二层、3人要求住一层、其余3人住任一层均可。那么要满足他们的住房要求且每人1间，有多少种不同的安排方案？（）

A.75 B.450 C.7200 D.43200

【答案】D【解析】由题干可知，邀请的专家中有4人明确要求住二层，因此可以先考虑这4个人的住宿情况，从二层的5个房间中选4个房间安排住宿，即接着有3人明确要求住一层，同理从一层的5个房间中选3个房间安排住宿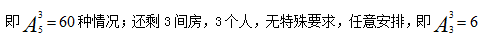，种情况；整个过程是分步完成的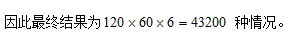，正确答案为D。

捆绑法

题型特征：题干中要求某些元素相邻。

捆绑法的使用：先将相邻元素捆绑成一个整体，再考虑这个整体与其他元素的顺序要求，最后考虑整体内部的顺序要求。

例2：一位同学买了4本不同的美术书，买了2本不同的历史书。他要把这6本书放在书架上，并且美术书都相邻，历史书也都相邻，问他有多少种不同的摆放方法？（）

A.48 B.96 C.120 D.720

【答案】B【解析】由题干可知，同类书籍要相邻摆放，因此可以将其捆绑在一起，看做一个整体，摆放时两类书籍一共有

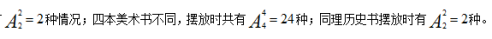整个过程分步完成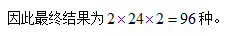，正确答案为B。

插空法

题型特征：题干中要求某些元素不相邻。

插空法的使用：先考虑其他元素的顺序要求，再将不相邻元素插到排好的空中。

例3：某单位为了丰富大家的业余生活，将8张同一排相邻的电影票发给了5个男生和3个女生，下班后这8位同事决定一同观影，若3个女生的座位互不相邻且不能在两端，问有多少种安排座位的方法？（）

A.40320 B.5040 C.2880 D.1440

【答案】C【解析】由题干可知，3个女生的座位互不相邻，因此可以先考虑男生座位的排列情况，属于5个人的全排列，一共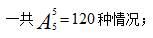男生排好之后一共产生了6个空，但是女生的座位不能在两端，因此可供选择的位置只剩下中间4个，从4个空位中选3个将女生排列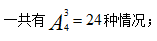，整个过程分步完成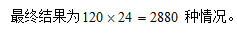，正确答案为C。

以上就是政华公考为大家带来的三种常用的解题方法，希望各位同学在平时做题过程中能够多加练习，真正做到融会贯通，熟能生巧。

行测数量关系：四大规律在手，方阵问题分数我有

方阵问题是行测数量关系中一类规律性较强的题型。清楚规律，做题会又快又准，不清楚规律，计算则会耗费大量时间。今天政华公考带大家来看一看方阵问题的这些规律以及规律的应用。

方阵问题的定义

方阵问题是指元素(人或物)按一定条件排成正方形(分为实心方阵和空心方阵)，根据方阵找到数据之间的规律，进而解决问题。

方阵的规律会围绕着：每条边上的元素个数n、每层的元素个数N、方阵的层数m、方阵的总元素个数M来展开。

核心规律

1.每层元素个数N=4×(n-1)

2.相邻层每边元素个数差2

3.相邻层元素个数差8(每边元素个数为奇数时，最内两层的元素个数差7)

4.实心方阵元素总数M=最外层每边元素个数的平方

经典例题

例1：参加阅兵式的官兵排成一个方阵，最外层的人数是80人，这个方阵共有官兵多少人？（）

A.441 B.400 C.361 D.386

【答案】A【解析】根据规律1，每层元素个数N=4×(n-1)，即80=4×(n-1)，可知最外层每边人数为21，再根据规律4，可得总人数为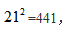选择A选项。

例2：在一次阅兵式上，某军排成了30人一行的正方形方阵接受检阅。最外两层共有多少人？（）

A.900 B.224 C.300 D.216

【答案】答案选B。已知最外层每边30人，根据规律1，最外层总人数为4×(30-1)=116人。根据规律3，相邻两层相差为8人，则次外层总人数为116-8=108人。最外两层共有116+108=224人。

例3：有一队士兵排成若干层的中空方阵，最外层人数共有60人，中间一层共44人，则该方阵士兵的总人数是（）。

A.156 B.210 C.220 D.280

【答案】答案选C。根据规律3，方阵相邻两层人数相差为8人，最外层为60人，中间一层为44人，可知中间一层为从外向内的第三层，里面还有两层，共5层，分别为60、52、44、36和28，共有220人，选择C选项。

对于方阵问题，只要能够掌握方阵的规律，并熟练运用，这种题型就比较容易解决。

行测数量关系：两步轻松解决年龄问题

年龄问题作为行测数量关系中的小众题型，难度不大，易于掌握。想要解好年龄问题，一方面要掌握年龄问题的特点，另一方面要用好合适的方法。政华公考在此进行展开分析。

第一步，搞懂年龄问题的特点——同增同减，差值不变

比如今年哥哥比弟弟大三岁，经过了n年，哥哥和弟弟的年龄都会增长n岁，此时哥哥依然比弟弟大三岁。

而解题时我们就可以利用这个特点来快速解题。

例1：甲今年44岁，乙今年16岁，当甲的年龄是乙的年龄的8倍时，二人的年龄和是多少？（）

A.24 B.36 C.48 D.52

【答案】B【解析】年龄问题中两个人的年龄差是不变的。所以今年甲是44岁，乙是16岁，甲比乙大28岁，那只要甲、乙存在(有可能会出现年龄小的还没出生的情况)，甲乙的年龄差就会保持28岁不变。所以当甲的年龄是乙的年龄的8倍时，设乙的年龄为x，甲的年龄就为8x，年龄差7x=28，解得x=4，此时两个人的年龄和为x+8x=9x=36岁，选择B选项。

第二步，用好工具事——表格+方程

当题目中涉及到的主体和年份比较多时，年龄问题就会变得比较复杂，此时通过列表的方式梳理好题干中条件之间的关系，有利于题目的求解。

例2；当弟弟像姐姐现在这样大时，姐弟俩的年龄和为26岁。明年，姐姐的年龄刚好为弟弟年龄的1.5倍，问现在弟弟多少岁？（）

A.4 B.5 C.6 D.7

【答案】D【解析】本题涉及到了两个主体：姐姐和弟弟。涉及到了3个时间：即现在、未来某年和明年，所以可以通过列表的方式梳理题干中的条件。设今年弟弟为x岁，姐姐为y岁，可得：

结合题干中的两个等量关系可得：2y-x+y=26…①，y+1=1.5×(x+1)…②，联立①②可解得x=7，y=11，所以现在弟弟为7岁。选择D选项。

所以，针对年龄问题，只要清楚年龄问题的特点和解题方法，并多加练习，这部分的分值就能拿到手。

行测数量关系：透析几何方向角问题

近几年来，在行测数量关系的考查中，有一种几何问题出现的频率稳步上升，其题干特点主要体现在：出现“东、南、西、北”并结合角度的方位描述，因需结合方位角度画图，让人无从下手，但是只要按照题中方向和角度画出图形，按照既定步骤便可求解。

步骤一：结合方位画出几何图形；

步骤二：结合图形中的方位角确定或构建直角三角形；

步骤三：把所求线段放在直角三角形中，并解直角三角形。

例题：一艘军舰以每小时20km的速度向东行驶，行驶A时看到一个灯塔C在北偏东60°处，军舰继续以原速向正东方向行驶，3小时后，到达B处，瞭望灯塔C，发现灯塔C在北偏东15°处，则此时军舰与灯塔的高距离为（）km。

【答案】B【解析】步骤一：结合题干描述方位画图如下：

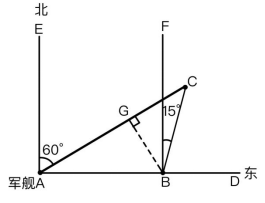
军舰最终行驶至B点，∠EAC=60°，∠CBF=15°，此题所求为军舰行至B处时与灯塔C的距离，即为BC。

步骤二：确定直角三角形，本题中无直角三角形，需构建直角三角形，作BG⊥AC，则△AGB、△BGC均为直角三角形。

步骤三：解直角三角形。

在Rt△AGB中，∠GAB=90°-∠EAC=30°，AB=20×3=60km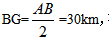，在△ABC中，∠C=180°-∠CAB-∠ABC=180°-30°-(90°+15°)=45°，则在Rt△BGC中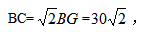，故本题选择B项。

几何方向角问题，牢记三步骤：一画，二直，三解；谨记顺口溜：方位画图是关键，构造直角当为先，特殊角度当用巧，线条长度马上现。

行测排列组合题的三种基本小方法

近年来，排列组合问题在各种公务员考试中出现的频率逐渐增加，排列组合作为数学运算中相对独立的一个知识点，一直被认为难度较高，因此许多考生对其望而却步，其实，只要考生掌握了排列组合问题相应的题型和解题方法，就能迎刃而解。今天政华公考带领大家学习排列组合问题中常见的三种基本小方法。

一、优限法：解决元素具有绝对位置限制要求的问题。特殊元素，优先处理；特殊位置，优先考虑。

例1：由数字1、2、3、4、5组成无重复数字的五位数，这五位数是奇数的情况有（）种。

A.24 B.36 C.48 D.72

【答案】D【解析】题目要求这五位数奇数，因此末位不能被2整除，可以使用优限法进行分析。优先考虑末位，在这里，末位有1、3、5这三个数字不能被2整除，因此末位有三种方法；之后再排其它位置，题干中其他位置没有特殊要求，所以是四个数字排在四个位置，由于交换两个数字的位置，会得到一个新的五位数，有顺序要求，因此是排列，这里先排末位再排其他位置，用乘法，所求为3×24=72。

二、捆绑法：解决元素相邻问题。元素要求相邻时，把相邻元素捆绑起来视为一个整体，再与其他元素进行排列，注意相邻的元素之间是否有顺序要求。

例2：由数字1、2、3、4、5组成无重复数字的五位数，所有奇数必须相邻的五位数有（）个。

A.36 B.48 C.60 D.72

【答案】A【解析】该题目要求所有奇数相邻，也就是1，3，5必须在一起，可以使用捆绑法进行分析。我们将1，3，5看成一个整体，也就是可以把1，3，5看成“一个数字”，再将这“一个数字”和剩下的2个数字进行排列，这样就相当于三个数字对应三个不同的位置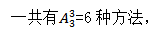，同时我们也要注意1，3，5这三个相邻的数字它们内部之间也有顺序要求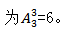，先考虑整体，再考虑捆绑内部，是一个分步过程，所求为6×6=36。

三、插空法：解决元素不相邻问题。有元素要求不相邻时，先处理除不相邻元素以外的部分，再找出能够插入的空位，将不相邻的元素插入到不同的空位中。

例3：由数字1、2、3、4、5组成无重复数字的五位数，两个偶数互不相邻的五位数有（）个。

A.48 B.60 C.72 D.84

【答案】C【解析】该题目要求两个偶数不相邻，也就是2，4不可以相邻，可以使用插空法进行分析。我们可以先把1，3，5排好，再把2和4插进1，3，5形成的四个空隙里面。首先1，3，5这3个数字对应三个位置，有顺序要求，一共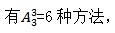接着再从四个空隙里面挑两个位置出来放2和4，同样需要考虑顺序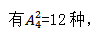，先排1，3，5再插2，4是分步的过程，用乘法，所求为6×12=72种。

政华公考相信大家通过以上三道题目，对于排列组合这三种方法有所了解，希望今后碰到同种类型的题目对大家有所帮助。