政华公考

【答案】B【解析】第一步，本题考查经济利润问题。第二步，根据题干中的百分数进行赋值，赋值改造前的日产量、能耗成本分别为10和2，则改造后的日产量和能耗成本则为9和1。假设其他成本为x，单件利润为y，则出厂价为3y，改造前，y=3y-2-x，改造后利润提高了10%，即9（3y-1-x）=1.1×10×y=1.1×10×（3y-2-x），解方程可得x=7，y=4.5。改造前能耗成本与其他成本的比值为2/7≈28.6%，在B选项的范围内。因此，选择B选项。

排列组合

排列组合问题可以理解成是一种计数问题，常见问法如做一件事有多少种方案、选法、方式等，掌握基础知识与常用方法能帮助我们灵活处理此类问题。

1.基础知识

排列

与顺序有关：

组合

与顺序无关:

如何判断有序或无序

从已选的主体中任意挑出两个，调换顺序：

（1）对结果有影响，与顺序有关（A）

（2）对结果无影响，与顺序无关（C）

2.常用方法

枚举法

（1）题型特征

选项数据不大

（2）解题思路

按照标准，从大到小一一枚举，不重不漏

捆绑法

（1）题型特征

题干要求元素相邻

（2）解题思路

①先捆：把相邻的元素捆绑起来，需要注意内部有无顺序；

②再排：将捆绑后的元素看成一个整体，与其他主体排列。

插空法

（1）题型特征

题干要求元素不相邻（不连续、不排在一起等）

（2）解题思路

①先排：先安排可以相邻的元素，形成若干空位；

②再插：再将不相邻的元素插入可以插的空位中。

插板法

（1）题型特征

N个相同元素分M堆，要求每堆至少分X个。

（2）解题思路

①先给每堆少分一个（即先分X-1个），此时剩N-M（X-1）个；

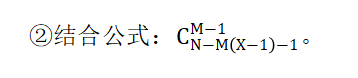
【例】某县通过发展旅游业来实现乡村振兴，引进了甲、乙、丙、丁、戊和己6名专家。其中甲、乙、丙是环境保护专家，丁、戊、己是旅游行业专家，甲、丁、戊熟悉社交媒体宣传。现要将6名专家平均分成2个小组，每个小组都要有环境保护专家、旅游行业专家和熟悉社交媒体宣传的人，问有多少种不同的分组方式（）？

A.12 B.24 C.4 D.8

【答案】D【解析】第一步，本题考查排列组合问题。

第二步解法一：因只分为2组，可使用枚举法。根据题目要求有（甲乙丁，丙戊己）、（甲乙戊，丙丁己）、（甲乙己，丙丁戊）、（甲丙丁，乙戊己）、（甲丙戊，乙丁己）、（甲丙己，乙丁戊）、（甲丁己、乙丙戊）、（甲戊己、乙丙丁）共8种分组方式。因此，选择D选项。

解法二：本题可使用平均分组模型进行求解。将6名专家平均分成2组，每组3人，有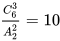种分组方式，但是要从其中排除掉不符合题意的2种情况，分别是（甲乙丙，丁戊己）和（甲丁戊，乙丙己），有10-2=8种分组方式。因此，选择D选项。

概率问题

概率问题是求一件事发生的可能性的一种题型，一般直接问概率是多少，往往与排列组合相结合考查，考查方式分为给情况求概率和给概率求概率两种题型。

【必背公式】

P=满足要求的情况数/总情况数

分类：P=P1+P2+…+Pn

分步：P=P1P2…Pn

正难则反：正面概率=1-反面概率

1.给情况求概率型

题型特征

题干给出若干情况，求某种情况的概率

解题思路

（1）求出总情况数和满足要求的情况数；

（2）结合公式：概率=计算。

注意：如果满足要求的情况数比较难求，则可从反面进行考虑，即正难则反：正面概率（满足要求的概率）=1-反面概率（不满足要求的概率、对立面概率）。

2.给概率求概率型

题型特征

题干给出具体的概率，求某种情况的概率

解题思路

先分情况讨论，再分别计算出每一类概率，最后将每种情况对应的概率进行加和计算

（1）分类：相加，P=P1+P2+…+Pn

（2）分步：相乘，P=P1P2…Pn

几何问题

周长公式

C正方形=4a C长方形=2（a+b）

C圆形=2πR

面积公式

S正方形=a2 S长方形=ab

S圆=πR2 S三角形=1/2ah

S平行四边形=ah S梯形=1/2（a+b）h

S扇形=n°/360°πR²

相似三角形性质

相似三角形对应线段的比等于相似比；

相似三角形周长的比等于相似比；

相似三角形面积之比为相似比的平方。

三角形不等式性质

两边之和大于第三边，两边之差小于第三边。

【例】下图中，三个同心圆的半径分别为1厘米、2厘米、3厘米，AB与CD垂直且过圆心O。那么图中阴影部分面积与非阴影部分的面积之比是多少（）

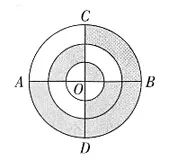
A.10:7 B.11:7 C.12:5 D.13:6

【答案】B【解析】将图中非阴影部分进行移动拼合后发现，非阴影部分可以看作由四分之一个大圆、四分之一个中圆和四分之一个小圆构成，面积为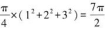平方厘米，阴影和非阴影部分的总面积为32×π=9π平方厘米，则阴影部分面积为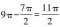，图中阴影部分面积与非阴影部分的面积之比为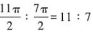故本题选B。