行测数量关系：轻松搞定植树问题和排列组合问题

行测数量关系规划小能手，到底需要“几棵树”

植树问题是公考行测考试里常出现的一个考点，在2019年广东省公务员考试中也曾考察过。这一类的题目本身难度不大、题目描述不复杂，只要我们掌握好解题方法再加以练习，相信大家都能在平时的练习及考试中从容应对。下面我们就一起来学习一下植树问题。

植树问题的原型是等距离植树类的题目，延伸出包括安装路灯，插旗杆，放花盆等一系列等距离间隔的问题。

首先，我们需要掌握植树问题的基础知识。植树问题的题目一般分为直线和环形两种类型：

一、直线上植树

方法总结：

1.两端都植树，树的棵数=(总长度/等间距长度)+1

2.一端植树一端不植树，树的棵数=总长度/等间距长度

3.两端都不植树，树的棵数=(总长度/等间距长度)-1

注意：上述都是道路单侧植树问题，有些题目要求可能是道路两侧植树，那么就需要在上述公式的基础之上再乘以2。

下面我们一起来练习一下直线上植树的题目：

例1：某城市天网建设，在一条主路上的一侧每隔4米设置一个摄像头，若这条主路上共有12个摄像头，且路的首尾两端都要装摄像头，那么这条主路的长度为（   ）米。

A.16       B.44         C.48           D.60

【答案】B【解析】根据题意，这条主路上共有12个摄像头，而且首尾两端都要安装，那么这条主路两端的摄像头之间共有12-1=11个间隔，每个间隔4米，那么这条主路的长度为4×11=44米。故本题选B。

例2：某公园在一条路的两侧植树，每隔10米种1棵。这条路总长100米，则最多可种树(    )棵。

A.12         B.14       C.18      D.22

【答案】D【解析】要想植的树最多，那么从端点就开始植树，优先思考两端植树的情况。根据公式：直线上植树(两端植树)棵数=总长度/等间距长度+1，此题是在路的两侧植树，故最多可种树棵树=(100÷10+1)×2=22棵。故正确答案为D。

二、环形植树(包括所有封闭图形，如：三角形，正方形，圆形，椭圆等)

方法总结：：树的棵数=图形周长/等间距长度

我们一起来练习一道环形植树的题目：

例3：某机构计划在一块边长为18米的正方形空地开展活动，需要在空地四边每隔2米插上一面彩旗，若该空地的四个角都需要插上彩旗，那么一共需要（   ）面彩旗。

A.32       B.36        C.44           D.48

【答案】B【解析】根据植树问题环形植树公式：树的棵数=图形周长/间隔长度=(18×4)/2=36。那么一共需要36面彩旗。故正确答案为B。

通过上述理论知识的学习和题目的练习，相信大家对于植树问题已经有了初步的认识，但要想在考试中游刃有余，还需要不断强化练习，提升能力，才能灵活应用。

行测数量关系：有规律的植树问题

数量关系在行测考试中之所以是大多数同学的难点，有的是因为题目过于灵活，情况多样，但也有的是因为不知道其解题原理，无从下手。而植树问题就属于相对固定、有规律可循的题目，只要我们掌握规律这类题目就迎刃而解了，那今天就让我们一起来学习一下吧。

公式

(一)开放空间植树问题公式

1.路不封闭且两端都植树：树的棵树=总路长/间距+1

2.路不封闭且两端都不植树：树的棵树=总路长/间距-1

3.路不封闭且只有一端植树：树的棵树=总路长/间距 

(二)封闭空间植树问题公式

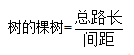
应用

例1：某厂一条主干道直通办公楼，路上一侧每隔8米装有一个路灯，办公楼门口有室外照明灯，小明从头到尾数了一下，一共有38个路灯。这条主干道长多少米？（   ）

A.296    B.300     C.304      D.312

【答案】C【解析】根据题意，办公楼门口不需要路灯，所以本题属于路不封闭且只有一端植树的变形问题，每隔8米装有路灯一个，即间距=8，根据公式有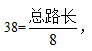总路长=38×8=304米，故本题选C。

例2：在一周长为50m的圆形花坛周围种树，如果每隔5m种一棵，共要种多少棵树？（   ）

A.10    B.11      C.12        D.15

【答案】A【解析】根据题意，本题属于封闭空间植树问题。已知每隔5m植树一棵，即间距=5，根据公式，则一共可以种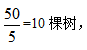故本题选A。

结合以上几道题的学习，大家已经对植树问题有了一定的了解，后续的练习一定要注意细节，尤其首尾两端是否“植树”。

行测数量关系考点：环形排列

排列组合题目，对于很多考生来说是数量关系中最头疼的问题，但其实排列组合当中有一类问题只要清楚它本身的方法，解决起来就会十分容易。接下来政华公考重点给大家介绍排列组合问题中的环形排列问题。

环形排列，顾名思义是指元素围成一圈，n个不同元素环形排列的情况数为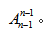

例1：甲、乙、丙、丁四个小朋友围成一圈，共有(   )种情况。

A.6      B.12       C.18        D.24

【答案】A【解析】四个小朋友围成一圈，即四个元素环形排列，总的情况数应为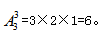

大家不免有疑问，为什么直线排列中n个元素排列的情况数为

我们一起思考一下，在直线排列中，以下为四种情况：

而在环形排列中，我们把以上四种情况按照顺时针排序：

不难发现以上四种情况元素之间相对位置并未发生变化，则在环形排列中为同一种情况。那就意味着如果我们直接用直线排列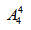去计算的话每一种情况都被重复计算了四次，所以环形排列的情况数应该为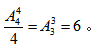将其推广至一般情况就有，环形排列中n个元素排列的情况数为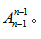

例2：10个小朋友围成一圈做游戏，问有多少种不同的坐法？（   ）

【答案】362880【解析】由题意可知。该题目属于环形排列问题，n=10，直接套用公式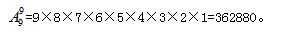

在考试中，环形排列时还会结合其他条件一起考查，我们只需要分析清楚其它条件，再使用环排公式即可。

相信通过本次环形排列问题的学习，大家对于此类型的题目有了一定的了解，但要想快速熟练地应用到考场，还需要各位考生勤加练习。

行测排列组合的四种常用方法

行测考试之中，数量关系是大多数考生的痛点也是难点，特别是排列组合问题更是让大家望而却步。但是对于这类题目，只要大家掌握一定的解题方法，问题就可以迎刃而解了。下面政华公考重点给大家介绍排列组合问题中常用的一些方法，并能够辨识每种方法的应用环境。

方法介绍

优限法：有特殊元素或特殊位置的排列问题，通常是先安排特殊元素或特殊位置，即优先处理特殊元素(或位置)法，简称优限法。

捆绑法：当出现元素相邻(或挨在一起等表述)时，先将相邻元素进行捆绑看作一个整体，再与其他元素进行排列，并且需要考虑被捆绑元素的顺序。

插空法：当出现元素不相邻(或不能挨在一起等表述)时，先将其他元素排好，再将所指定的不相邻的元素插入到他们的间隙或两端位置。

间接法：在解决至多至少等问题时，正向求解比较复杂，我们可以反向求解，用总的方法数减去对立面(反面)的方法数即可得到我们的所求。

方法应用

例题：由数字1、2、3、4、5组成无重复数字的五位数，

(1)数字1必须在首位或末尾的五位数有________个。

(2)两个偶数必须相邻的五位数有________个。

(3)两个偶数互不相邻的五位数有________个。

(4)至少有一个偶数在前两个位置的五位数有________个。

【答案】48；48；72；84【解析】

(1)数字1有特殊要求，则先排数字1，有2种；再排其余数字，有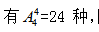因此所求为2×24=48个。

(2)2个偶数必须相邻，则将2个偶数捆绑在一起看成1个数，与剩余的3个数进行排列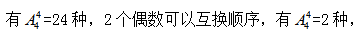，故所求为24×2=48个。

(3)先排3个奇数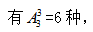，再从奇数形成的4个空位里选2个将剩余2个偶数放入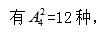，因此所求为6×12=72个。

(4)两个偶数中至少有一个在前两个的位置，即包含了有一个或者是两个均在前两个位置中，情况较多，不太容易求解，故考虑用间接求解，即总的方法数-反面方法数=所求方法数。总的方法数为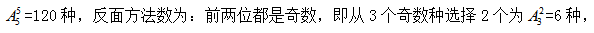：故为6×6=36种，所求为：120-36=84种。

例题展示

例1：有8人要求在某学术报告会上做报告，其中甲、乙要被安排在前三个，丙要在最后一个，丁不在前三个，则共有多少种可能的报告顺序？（   ）

A.553         B.576      C.283        D.266

【答案】B【解析】甲、乙要在前三，可以优先安排他们的顺序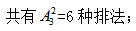，其次，丙在最后一个，共有1种排法；最后丁不在前三个，同时也不可能是最后一个，所以只有中间四个位置可以选择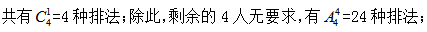，因此所求为：6×4×24=576种顺序，故选择B项。

例2：为加强机关文化建设，某市直机关在系统内举办演讲比赛，3个部门分别派出3、2、4名选手参加比赛，要求每个部门的参赛选手比赛顺序必须相连，问不同参赛顺序的种数在以下哪个范围之内？（   ）

A.小于1000       B.1000~5000        C.5001~20000     D.大于20000

【答案】B【解析】每个部门的参赛选手比赛顺序必须相连，即将每个部门的人进行捆绑，看作一个整体，即共3个部门；首先考虑三个部门的出场顺序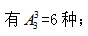，其次考虑每个部门选手的出场顺序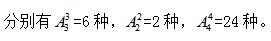，则不同参赛顺序的种数为6×6×2×24=72×24，计算结果显然大于1000，小于5000，故选择B项。

以上便是政华公考介绍的关于排列组合问题的一些常见方法以及求解思路，值得注意的是，在做这类问题的时候，需要我们理解每种方法的应用场景，而很多题目往往要同时用到多种方法，这就更需要我们熟练运用这些方法，所以同学们还要加强练习。

行测数量关系：如何巧解排列组合异素分堆问题

排列组合问题是行测考试中必考内容，其中的异素分堆问题备受命题人青睐，这类题目难度很大，很多考生在做题中缺乏做题思路，殊不知这类题是有技巧的，政华公考在本文中对异素分堆问题的常见考法的解题思路进行梳理，相信大家看了本文，此类题就会成为你的“得分点”。

异素非均分

例题1：将编号1到9的9个小球，按照2个、3个、4个的数量分成3堆，有多少种分法？（   ）

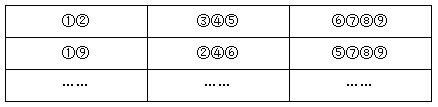
【答案】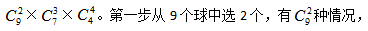第二步从余下球中选3个，由于是分步计算，

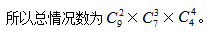
例题2：将编号1到9的9个小球，按照2个、3个、4个的数量分给3个人，有多少种分法？（   ）

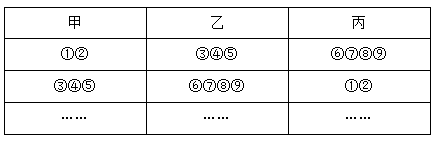
【答案】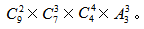首先第一步还是可以按照上道题去先把这9个球分成三堆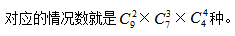，但是因为这个题分堆后还需要再分给3个人。甲拿①②，乙拿③④⑤，丙拿⑥⑦⑧⑨和甲拿③④⑤，乙拿⑥⑦⑧⑨，丙拿①②属于不同情况，所以需要考虑顺序，

异素非均分小结：(1)如果每堆元素无需再进行分配，则不需要考虑顺序。(2)如果每堆元素需要再进行分配，则需要考虑顺序，需乘上堆数的全排列。

异素均分

例题3：将编号1到9的9个小球，平均分成3堆，有多少种分法？（   ）

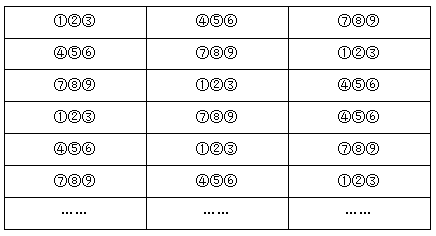
【答案】真有这么多种吗？其实不然，根据上表来分析，这6种情况都是属于同一种分组情况，即①②③一组，④⑤⑥一组，⑦⑧⑨一组。所以我们重复算了6次。

例题4：将编号1到9的9个小球，平均分给3个人，有多少种分法？（   ）

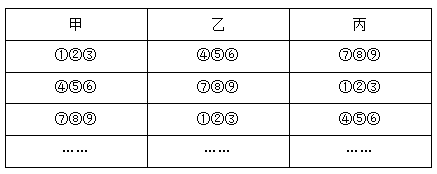
【答案】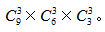因为题干要求平均分给3人，也就是每人分3个球。我们可以先按照上题分成3堆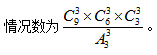，因为还需要分给三个人，故还需要

异素均分小结：(1)如果每堆元素需要再进行分配，则需要考虑顺序，组合数的列式已包含顺序。(2)如果每堆元素无需再进行分配，则不考虑顺序，需除以堆数的全排列。

以上就是异素分堆的总结，备考过程中要多对复杂题目进行总结，掌握做题方法，针对性的解决问题。