政华教育

【答案】B【解析】最终要求的总时间应该是由灌水时间和排队等待的时间组成的，而其中三个人灌水所花的时间是固定的，那我们要让总时间最少，就得让三位同学等待的时间尽可能地短。之所以会产生等待的时间，是因为我们只有一个水龙头，就意味着第一个人在灌水的时候，另外两个人是需要等待的，所以我们要让等待的时间尽可能地短就要研究一下三位同学灌水的顺序：如果第一个灌水的是甲同学，他灌水需要1.5分钟，那就意味着乙、丙同学分别都要等待1.5分钟;如果第一个灌水的是乙同学，他灌水需要0.5分钟，就说明剩下的甲、丙两位同学分别都要等待0.5分钟;如果第一个灌水的是丙同学，他灌水需要1分钟，就意味着甲和乙分别要等待1分钟。对比这三种情况我们会发现第一个灌水的是乙同学就可以保证另外两个人等待的时间最短，也就说明我们解决排队取水问题的原则就是：让取水时间短的优先取水，即谁花的时间短谁先来。

因此三个人排队灌水的顺序应该是乙、丙、甲，具体灌水和等待的时间如下表所示：

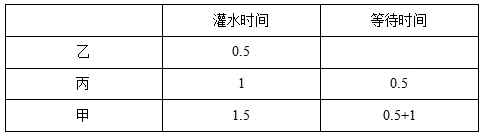
通过观察上表会发现0.5出现了三次，1出现了两次，1.5出现了一次，所以时间总和最短为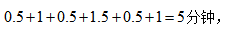故本题选B。

总结：排队取水问题的解题原则为：让取水时间短的优先取水。

【思考】如果在上面例题的基础上，我们稍微增加一些条件，把题干中的“甲乙丙”三位

同学变成“甲乙丙丁戊己庚”六位同学，已知他们灌水所需的时间分别为1.5分钟、0.5分钟、1分钟、2分钟、3分钟和5分钟，六人同时到一个公用的水龙头灌水，这样花费的时间总和最少是多少呢？

题目辨析：根据解题原则，我们可以首先确定这六位同学的打水顺序为乙、丙、甲、戊、己、庚，具体灌水和等待的时间如下表所示：

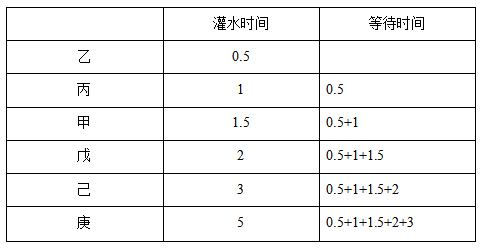
通过观察上表我们会发现每一个灌水时间都多次出现，那我们可以汇总一下：0.5出现了六次，1出现了五次，1.5出现了四次，2出现了三次，3出现了两次，5出现了一次，所以时间总和最少为

总结：上面两道题目最终的算式中都涉及到了所有人的打水时间，解决排队取水问题可以分成两步走：第一步，按照打水所需时间将时间从大到小依次排开;第二步，按照从1开始的自然数与排好的顺序依次相乘。

政华公考相信通过今天的讲解，大家对于排队取水问题已经有了一定的了解，大家能够在复习的过程中再找几道题目巩固一下，这样在考试中出现此类问题时就能够快速求解。

行测数量关系：年龄其实挺简单，掌握核心容易算

在行测数量关系当中年龄问题是比较常见的一种题型，它主要研究两个或多个主体在不同时期的年龄关系。年龄问题中隐藏着一个等量关系——年龄差不变，即任意两人的年龄差，不管过多少年始终保持不变，这也是解决年龄问题的核心，只要掌握了这一核心，年龄问题的求解都会比较简单。

下面我们一起通过例题来感受一下吧。

例1：甲、乙两人的年龄和正好是80岁，甲对乙说：“我像你这么大时，你的年龄正好是我年龄的一半。”甲今年（）岁。

A.32 B.40 C.48 D.45

【答案】C【解析】设甲今年X岁，则乙今年(80-X)岁，根据题意有如下表格，

根据年龄差不变有解得X=48。故正确答案为C。

总结：通过上述例题不难发现，题中不同时间的甲、乙年龄均未知，为了更好地整理题干信息，我们可通过列表的方式进行呈现，这样不同主体间关系非常清晰，进而通过年龄差不变列式求解。这里提醒大家，列表是年龄问题常用的梳理题干的方法。

例2：2018年父亲年龄是女儿年龄的6倍，是母亲年龄的1.2倍。已知女儿出生当年(按0岁计算)母亲24岁，则哪一年父母年龄之和是女儿的4倍？（）

A.2036 B.2039 C.2042 D.2045

【答案】B【解析】设2018年女儿的年龄为X岁。通过列表梳理题干信息如下：

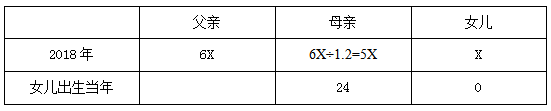
根据母亲和女儿的年龄差不变可得，5X-X=24-0，解得X=6。所以2018年父亲36岁，母亲30岁，女儿6岁。设n年后父母年龄之和是女儿的4倍，则有36+n+30+n=4×(6+n)，解得n=21。2018+21=2039，即2039年父母年龄之和是女儿的4倍。故正确答案为B。

通过上述例题，相信大家对解决年龄问题的核心比较熟悉了。政华公考希望各位小伙伴们多加练习，能得心应手、游刃有余地解决年龄问题。

行测数量关系：错位重排问题

排列组合问题由于出题比较灵活，所以对很多考生来说很难驾驭，平时大家测试时遇到排列组合问题有可能会故意避开。但是排列组合问题中也有一些比较具备典型特征的题目，而且解题方法比较固定，比如错位重排问题。在行测考试中如果错失这类题目的分数，还是比较可惜的，今天政华公考就带领大家一起学习如何求解错位重排问题。

题型特征

错位重排问题是伯努利和欧拉在错装信封时发现的，因此又称为伯努利-欧拉装错信封问题。错位重排从字面意思理解，就是排错了位置，所以它的基本特征就是每个元素不回到原本的位置。比如：编号是1、2、…、n的n封信，装入编号为1、2、…、n的n个信封，要求每个信封装一封信且每封信和信封的编号不同，问有多少种装法？

方法介绍

①当信1放入信封2时，如下图所示：

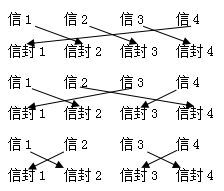
当信2放入信封3或4时有2种，当信2放入信封1时有1种，共2+1=3种;

②当信1放入信封3，情况同①，共2+1=3种;

③当信1放入信封4，情况同①，共2+1=3种。

经典例题

例1：六年级有四个班级，期末考试来临，四个班的四位班主任组成监考小组，每位班主任监考一个班级，若要求每位班主任不能监考自己的班级，则四位班主任组成的监考情况有多少种？（）

A.6 B.7 C.8 D.9

【答案】D【解析】四位班主任每人监考一个班级且不能监考自己的班级，相当于4个元素的错位重排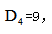，故一共有9种监考情况，选择D项。

例2：机场的行李传送带上还剩下五位旅客的外观一样的行李箱，每人一个，请问恰有2人取到自己的行李箱的情况有多少种？（）

A.20 B.22 C.24 D.28

【答案】A【解析】根据题意，第一步从五位旅客中选出2位旅客取到自己的行李箱，一共有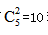种情况，第二步是剩下3人都没有取到自己的行李箱，相当于3个元素的错位重排问题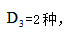，故一共有10×2=20种情况，选择A项。

以上就是行测错位重排问题，政华公考相信大家认识这类题型记住结论了，赶快做题试一试吧!

行测数量关系简单易上手之多者合作

在近年来的行测考试数量关系中，工程问题出现频率较高，且难度不大。重点考查对于基本解题方法的掌握。那么今天，政华公考带着大家一起了解一下工程问题中较为常见的考点——多者合作。

题型特征

多者合作是指多个主体通过一定合作方式完成工作的问题。题干具备描述不同合作方式的典型特征，所以我们可以借助梳理不同合作方式，并结合工作量一定来建立等量关系来解决此类问题。

解题方法

常用的方法是特值法。特值法是指将题干中参与计算的过程量用具体数值来表示，从而达到简化计算目的的一种方法。

主要分为以下三种设特值的方式：

1.已知多个主体完工时间时，可设工作总量为1或完工时间的公倍数。

2.已知多个主体效率关系时，一般根据效率关系将效率设为最简比的数值。

3.已知多个主体的效率相同时，一般设每个主体的效率为1。

例题解析

例1：一个工程项目，甲公司单独做需要8天能完成，乙公司单独做需要12天，甲、乙、丙三个公司4天能完成，则由甲、丙公司合作完成此项目共需多少天？（）

A.5 B.6 C.7 D.8

【答案】B

思考：在计算过程中发现工作总量x在最后的运算过程中被约去了，并不影响实际计算结果，那么我们是否可以把工作总量设为具体数值方便计算呢？

例2：甲工程队与乙工程队的效率之比为4：5。一项工程由甲工程队单独做6天，再由乙工程队单独做8天，最后由甲乙两个工程队合作4天刚好完成。如果这项工程由甲工程队或乙工程队单独完成，则甲工程队所需的天数比乙工程队所需的天数多几天？（）

A.3 B.4 C.5 D.6

【答案】C【解析】结合题干中给出甲乙效率比，结合份数思想，便可设两者工作效率分别为4x、5x，则这项工程的工作总量为4x×6+5x×8+(4x+5x)×4=100x。甲工程队单独完成需要100x÷4x=25天，乙工程队单独完成需要100x÷5x=20天，所求为25-20=5天，故本题选C。

思考：同样的，这道题目中x在运算中也被约掉，是不是也可以将甲乙效率直接特具体数值简化运算呢？

【解析】设甲与乙的工作效率分别为4、5，则这项工程的工作总量为4×6+5×8+(4+5)×4=100。甲工程队单独完成需要100÷4=25天，乙工程队单独完成需要100÷5=20天，所求为25-20=5天，选C。

例3：修一条公路，假设每人每天的工作效率相同，计划180名工人12天完成。工作4天后，因特殊情况，要求提前2天完成任务。则需要增加多少名工人？（）

A.50 B.65 C.70 D.60

【答案】D【解析】题干中每人每天的工作效率相同，则可设每名工人每天的工作效率为x，则全部的工作总量为180×12x，工作4天完成的工作量180×4x。设要想提前2天完成任务，则需要增加工人a名，则有180×4x+(180+a)×(12-4-2)x=180×12x。解得a=60。故本题选D。

思考：此题x被约掉，其数值仍不影响最终结果，仍然可以利用特值法求解!

【解析】设每名工人每天的工作效率为1，则全部的工作总量为180×12，工作4天完成的工作量180×4。设要想提前2天完成任务，则需要增加工人x名，则有180×4+(180+x)×(12-4-2)=180×12。解得x=60，选D。

相信大家通过这次政华公考对多者合作的讲解，对这类问题有了更清晰的了解。重点学会以上三种特值法在多者合作问题中的应用，多多练习，熟能生巧，才能真正做到简单易上手!

行测数量关系：整除，让你更快地解题

数量关系是行测考试中能拉开分差的题型，与言语理解与表达、判断推理、资料分析等题目相比，数量关系知识点多，解题比较耗时，但是只要掌握相应的解题方法，还是能够快速选出答案的，比如整除特性的巧妙应用。接下来就让政华公考带领大家打开整除特性的知识大门。

整除的定义

若a÷b=c(a、b、c均为整数，且b≠0)，则a能被b整除，或b能整除a。

整除的核心

通过题干信息，分析出整除特性，从而排除错误选项或确定某个未知量。

整除关系的确定

1.文字体现整除：整除、平均、每、倍数。

2.数据现整除：分数、百分数、比例。

例题详解

例题1：某部门租车出游，平均每人应付车费42元。后来又增加了若干人，这样每人应付的车费是33元，租车费是（）。

A.1265元 B.2024元 C.2772元 D.3165元

【答案】C【解析】结合题干信息“平均每人应付车费42元”和“每人应付的车费是33元”，又根据“总车费=平均每人应付车费×人数”，可确定租车费能被42和33整除。42和33均是合数，则有42=2×3×7，33=3×11，即租车费能被2、3、7和11整除，能被2和3整除可排除A、B、D选项。故本题选C。

点拨：题干中有特殊文字“平均”、“每”、“倍数”、“整除”等描述时，一般可确定整除关系，结合相关数字的整除判定方法快速排除选项确定答案。

例题2：某单位原拥有中级及以上职称的职工占职工总数的62.5%。现又有2名职工评上中级职称，之后该单位拥有中级及以上职称的人数占总人数的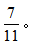则该单位原来有多少名职称在中级以下的职工？（）

A.68 B.66 C.62 D.60

【答案】B【解析】结合题干信息可知，该单位原拥有中级以下职称的职工占职工总数的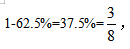即该单位原拥有中级以下职称的职工能被3整除，排除A、C项。又有2名职工评上中级职称后该单位拥有中级以下职称的人数占总人数的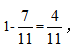即该单位原拥有中级以下的职工减去2后，能被4整除，排除D选项。故本题选B。

点拨：题干中有特征数据“百分数”、“分数”、“比例”等描述时，一般可确定整除关系，结合相关数据的整除判定方法快速排除选项确定答案。

通过政华公考以上题目的分享，希望大家养成习惯，题干中出现可以确定整除关系的特殊文字或特征数据相关描述时，可以优先考虑能否利用整除确定选项，或者确定某个未知量，简化计算过程和计算量，提高答题效率。