行测数量关系：排列组合常用方法
行测数量关系：排列组合常用方法
在公务员行测考试的数量关系题目中，排列组合问题是一类很重要的题型，而其通常伴随一些明显的特征出现。今天，政华公考就通过本文为大家介绍排列组合的常用方法。
优限法
1.应用环境：要求元素必须在哪儿或不在哪儿，即对元素的绝对位置有要求。
2.操作方法：首先把有绝对位置要求的元素优先进行排列组合，然后考虑其他元素的排列组合情况。
例1：一次会议某单位邀请了10名专家，该单位预定了10个房间，其中一层5间、二层5间。已知邀请专家中4人要求住二层、3人要求住一层、其余3人住任一层均可。那么要满足他们的住房要求且每人1间，有多少种不同的安排方案？（ ）
A.75 B.450 C.7200 D.43200
【答案】D【解析】由题意，专家中有4人要求住二层、3人要求住一层，他们有绝对的位置要求，那么此题应当采用优限法来解题。共有10人，4人要求住二层，
其余3人安排住剩下的3个房间，
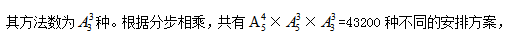故本题选D。
捆绑法
1.应用环境：有元素要求“相邻”。
2.操作方法：首先把要求“相邻”的元素捆绑起来视为一个整体，与其他元素进行排列组合，然后考虑捆绑元素内部的顺序。
例2：为加强机关文化建设，某市直机关在系统内举办演讲比赛，3个部门分别派出3、2、4名选手参加比赛，要求每个部门的参赛选手比赛顺序必须相连，问不同参赛顺序的种数在以下哪个范围之内？（ ）
A.小于1000 B.1000—5000
C.5001—20000 D.大于20000
【答案】B【解析】由题意，每个部门的参赛选手比赛顺序必须相连，即元素要求“相邻”，采用捆绑法。首先把3个部门的选手分别捆绑在一起，考虑三个部门的出场顺序，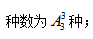
然后考虑每个部门内部各选手的出场顺序，
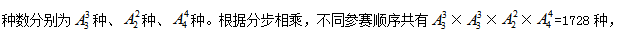计算结果显然大于1000，小于5000。本题选B。
插空法
1.应用环境：有元素要求“不相邻”。
2.操作方法：先把其它可相邻的元素进行排列组合，形成空，然后将不相邻的元素进行插空。
例3：把12棵同样的松树和6棵同样的柏树种植在道路两侧，每侧种植9棵，要求每侧的柏树数量相等且不相邻，且道路起点和终点处两侧种植的都必须是松树。问有多少种不同的种植方法？（ ）
A.36 B.50 C.100 D.400
【答案】C【解析】由题意，每侧的柏树要求不相邻，采用插空法。道路每侧种植9棵树，其中6棵松树3棵柏树，6棵松树形成5个空隙，将3棵柏树插入，
本题选C。
以上就是排列组合的几种常用方法，大家具体解题时一定要看清题干中的各种限制条件，明确哪种条件下该使用哪种方法，做到熟能生巧。
行测排列组合之异素均分问题易错点剖析
数量关系是行测考试中难度颇高的一个板块，其主要考察应试者理解、把握事物间量化关系和解决数量关系问题的技能，主要涉及数字和数据关系的分析、推理、判断运算等，其中，排列组合的异素均分问题是很多同学都很难做正确的一类题目，但只要我们研究清楚其问题的本质，便可轻松做对此类题目。
一、从问法上识别“异素均分”问题
异素均分，就概念而言，就是把不同的元素进行平均分组。
例如：m个不同的元素，平均分为n个组，一共有多少种情况？
二、“异素均分”问题破解思路
把m个不同的元素平均分成n组，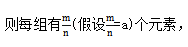
接着我们采用分步的原理来计算，首先从m个元素当中取出a个元素，接着从剩下的元素当中再取出a个元素，一直重复下去，每次都取a个元素，等到全部元素取完便可终止，最后再分析这个过程中所包含的情况数。
1.异素均分分堆问题
例1：某中学有8个运动员，要平均分成2组，一共有几种分法？（ ）
A.25 B.70 C.35 D.90
【答案】C【解析】8个运动员平均分成2组，每组4人。首先从8个运动员中选出4个人，
接着从剩下的4个人中选出4个人，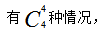
因为整个过程是分步进行的，所以总的方法数等于各个步骤的方法数相乘，
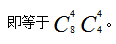但其实这样做是存在问题的，我们可以把这8个人用abcdefgh这8个字母依次来表示，其中的一种情况可以是abcd为一组，那么剩下的efgh就自然成为另外一组了，当然也有可能是先挑出了efgh为一组，则abcd为一组，这两种分组方式前后对比会发现是同一种分组方式，都是abcd为一组，efgh为一组，所以算重复了2次，实际上的情况数为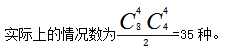
通过这个题目我们可以看出，平均分成2组，算重复了2次，如果平均分成3组，会算重复几次呢？
例2：将红、橙、黄、绿、蓝、白6颗不同颜色的玻璃球，平均分成3堆，一共有几种情况？（ ）
A.15 B.45 C.60 D.90
【答案】A【解析】6颗不同颜色的玻璃球等同于6个不同的元素，平均分成3堆，每堆2颗玻璃球。首先，从6颗玻璃球中取出2颗；接着从剩下的4颗玻璃球中取2颗；最后从剩下的2颗中选出2颗，同样的我们还是选取其中的一种情况(红橙、黄绿、蓝白)来分析。
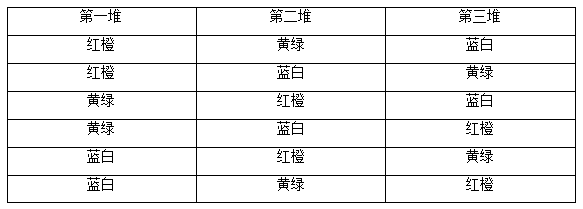
通过这个表格的简单罗列，我们便可以清楚地发现这6种情况都是同一种分堆情况，即红橙一堆，黄绿一堆，蓝白一堆，算重复了6次，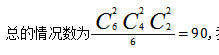
我们可以进一步总结前一个题目平均分成两组，算重复了2次，本质上是算重复了
本题平均分成3组，算重复了6次，
所以可以得到异素均分问题平均分成n组，
2.异素均分分配问题
例题：某公司将旗下的6名歌手两两组成一个队，到三个不同的省会城市参加巡演，共有多少种不同的巡演情况？（ ）
A.15 B.45 C.60 D.90
【答案】D【解析】本题为异素均分问题，6名歌手两个人为一个队，即平均分成3队。根据前面所讲分成3队，
因为3个队是去到3个不同的城市巡演，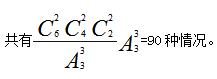
相信大家通过上述题目，能对异素均分问题有所了解，建议大家在备考期间多多练习，真正掌握这类问题，也希望能对大家的备考有所帮助。
行测排列组合不用烦，隔板模型记心间
在行测数量关系考试中，排列组合是很多人又爱又恨的一个考点，对文科生来讲尤其如此，爱它是因为计算量相对不大，恨它是因为计数时经常出现重复或遗漏的情况。其实排列组合中的一些问题是有固定解题思路的，也有一些常见的解题模型。本文接下来政华公考就给大家分享排列组合中一种特殊模型——“隔板模型”。
“隔板模型”的特征是：n个相同元素分给m个不同对象，每个对象至少分一个元素，求所有可能的分法。“隔板模型”的解题思路是：将n个元素排成一排，在n个元素之间形成的n-1个间隙中放置m-1块隔板，即可把它隔成m份，这样所有不同的插入方法就是n个相同的元素分给m个不同对象的所有情况数，为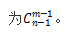
例1：共有10本完全相同的书分到4个班里，每个班至少要分到一本书，共有几种不同分法？（ ）
A.84 B.75 C.64 D.45
【答案】A【解析】先将10本相同的书排成一排，10本书之间出现了10-1=9个空隙，现在我们用4-1=3个挡板插入这9个空隙中，就把10本书隔成4份，正好分给4个班级；从9个空选3个插入3个相同挡板，不考虑顺序，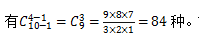
故正确答案为A。
例2：共有6本完全相同的书分到4个班里，共有多少种不同分法？（ ）
A.84 B.75 C.64 D.45
【答案】A【解析】由于会有不放书的班级，因此需要将问题转化为标准的隔板模型。先从每个班级借一本书，则现在有10本书，问题就转化为“将10本完全相同的书分给4个班，每班至少分到一本”。从10本书排成一排所形成的10-1=9个空隙里选择3个空隙插入隔板，就把10本书隔成4份，正好分给4个班级，每个班至少一本书，则不同的分法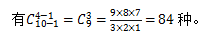
故正确答案为A。
例3：共有14本完全相同的书分到4个班里，每个班至少分到两本书，共有多少种不同分法？（ ）
A.84 B.75 C.64 D.45
【答案】A【解析】由于每个班级至少分两本，因此需要将问题转化为标准的隔板模型。每个班级先发1本书，还剩10本，则问题转化为“将10本完全相同的书分给4个班，每班至少分到一本”。从10本书排成一排所形成的10-1=9个空隙里选择3个空隙插入隔板，就把10本书隔成4份，正好分给4个班级，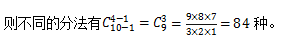
故正确答案为A。
通过上面三个例子对比，大家会发现虽然下面两个例子与“隔板法”题型特征不符，但是我们可以通过转换使其满足条件，最终还是可以借助公式来解题。
通过对上述例题的学习，大家应该已经能够感受到数学变化的神奇。希望同学们在平日的学习中能够多多练习，真正把所学方法内化于心，外化于行，做到信手拈来！
