政华教育

首先同学们需要先了解交替合作的题型特征：交替合作问题一般指多个主体共同完成某一工程，在合作过程中按一定规律来轮流工作，所以工程问题中出现按顺序、轮流等字眼的时候，我们一般都把它当成交替合作的题目来进行求解。它的解题思路可以总结为以下几步：1、设工作总量为特值并表示出效率。2、找到最小循环周期、周期峰值、周期内工作量之和。3、算出周期数和工作余量。4、分配工作余量并算得时间。下面我们通过例题来进行学习。

例1：一项工程，甲单独做需要10小时完成，乙单独做需要6小时完成。现在甲乙合作，先由甲做1小时，再由乙做1小时的方式轮流工作，完成这项工程需要多少时间？（）

A.6小时30分钟 B.7小时 C.7小时36分钟 D.8小时

【答案】C【解析】设工作总量为30，则甲的效率是3，乙的效率是5。甲乙轮流每人工作1小时，可得最小循环周期为2小时，周期内工作总量为3+5=8。30÷8=3……6，3个周期为6小时，剩下6的工作余量需要甲再工作1小时，工作量为3，最后剩下的6-3=3的工作量需要乙做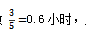所以最终完成工作的时间为6+1+0.6=7小时36分钟。故本题答案C。

例2：一项工程，甲单独做需要10小时完成，乙单独做需要8小时完成，丙单独做需要6小时完成，现在甲乙丙合作，先由甲做1小时，再由乙做1小时，再由丙做1小时的方式轮流工作，完成这项工程需要多少时间？（）

A.7小时24分钟 B.7小时32分钟 C.7小时40分钟 D.7小时56分钟

【答案】D【解析】设工作总量为120，甲的效率12，乙的效率15，丙的效率20。甲乙丙轮流每人工作1小时，可得最小循环周期为3小时，周期内工作总量为12+15+20=47。120÷47=2……26，2个周期为6小时，剩下26的工作量需要甲再工作1小时，工作量为12，最后剩下26-12=14的工作量需要乙做所以最终完成这项工程的时间为7小时56分钟。故本题选D。

以上两题都是只有正效率的情况，接下来我们看一下存在负效率的时候怎么求解。这两种题目最大的区别就在于，存在负效率的时候需要预留周期峰值。

例3：有一个水池，甲进水管装满要4小时，乙进水管装满要6小时，丙出水管排空要8小时，现在甲乙丙3根水管轮流开水，每次1小时，问需要多少时间水池才能装满？（）

A.8 B.9 C.10 D.11

【答案】A【解析】设工作总量为24，甲乙为进水记为正效率，丙为放水记为负效率，所以甲效率6，乙效率4，丙效率为-3。甲乙丙各轮流工作1小时，可得最小循环周期为3小时，周期内工作总量为6+4-3=7，周期峰值为6+4=10。由于最后一小时为丙工作，丙是放水，所以工作过程中需要预留周期峰值24-10=14，14÷7=2。2个周期为6小时，剩下10的工作量需要甲和乙各工作1小时，所以最终装满水池需要的时间为6+1+1=8小时，本题答案选A。

通过上面这几道例题，相信同学们对于交替合作的问题已然了解清楚，接下来还需要同学们再进行针对性地加强训练，掌握好这类题目。

翻越行测数量关系“大山”的垫脚石——工程问题

行测数量关系中的工程问题，其基础计算公式是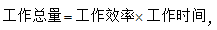常考题型包括普通工程和多者合作。多者合作问题即从工作时间入手，把工作总量设为“时间们”的最小公倍数。今天，政华公考继续为大家介绍多者合作问题中特值法的另一种应用，即从工作效率入手，先找出“效率们”的最简比，将最简比直接设为效率。

接下来，让我们通过例题更好地了解一下。

例题1：一项工程由甲、乙、丙三个工程队共同完成需要15天，甲队与乙队的工作效率相同，丙队3天的工作量与乙队4天的工作量相当。三队同时开工2天后，丙队被调往另一工地，甲乙两队留下继续工作。那么，开工22天后，这项工程：（）

A.已经完工 B.余下的量需甲乙两队共同工作一天

C.余下的量需乙丙两队共同工作一天 D.余下的量需甲乙丙三队共同工作一天

【答案】D【解析】由于丙队3天的工作量与乙队4天的工作量相当，可得丙与乙的效率比为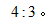不妨假设丙队每天的工作量为4，乙队每天的工作量为3，则甲队每天的工作量为3。这项工程总的工作量为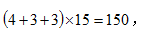则工作22天后，工程还剩下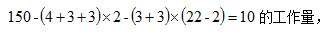正好让甲、乙、丙三队共同工作一天。选择D项。

例题2：有一项工作任务，小明先做4小时，小方接着做9小时可以完成，小明先做6小时，小方接着做5小时也可以完成，如果小明先做2小时后再让小方接着做，那么小方完成这项工作还需要几个小时？（）

A.9 B.11 C.12 D.13

【答案】D【解析】由题干信息可知，小明多做2个小时，小方就少做4个小时，小明做2个小时的工作量等于小方做4个小时的工作量，所以小明和小方的效率之比是2：1，于是可直接设小明每小时的工作量是2，小方每小时的工作量是1，则推出工作总量是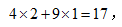小明做2小时后还剩17-2×2=13的工作量，则小方完成这项工作还需要13÷1=13小时，选择D项。

小结：在多者合作中，已知多个主体效率关系时，一般将最简比设为效率，进而求出工作总量。

通过以上例题讲解，相信大家对如何应用特值法解决多者合作问题有了一定了解，在考试中可以优先选择此类问题作答。

对于多者合作问题可以结合已知条件利用特值法进行求解。之所以把工程问题比喻成垫脚石，是因为它较容易理解。

行测数量关系中似是而非的“多者合作”---多劳力合作

在行测数量关系多者合作问题中有一类问题为多劳力问题，其和普通多者合作问题的区别是这类题目往往求的是最优的结果。其本质是统筹问题，是研究人力、物力的运用和筹划，使它们能发挥最大效率的一类问题。

一、什么是多劳力合作问题

怎样用最少的人力、物力在最短的时间内完成一定的任务或是怎样用一定的人力、物力在一定时间内完成更多的任务量。

二、多劳力合作问题的解题原则

使每个劳动力发挥各自所长，统筹安排，方能实现最优，简单来说，也就是让合适的人做合适的事。这类问题的关键在于如何确定相对擅长项，我们结合相关题目来了解一下：

(一)已知每人完成各项工作的效率

例1：甲和乙手工制作一种杯子的杯身和杯盖，杯子只由这两部分组成。甲每天可以制作150个杯身，或者制作75个杯盖；乙每天可以制作60个杯身，或者制作24个杯盖。现两人一起合作制作杯子，10天最多可以制作（）件杯子。

A.600 B.650 C.700 D.900

【答案】C【解析】每个杯子由一个杯身和一个杯盖组成，若让最终杯子最多，那么杯子和杯盖的数量都尽可能多，且数量均可匹配无剩余为最理想状态。所以最终制作两部分的数量最大且相等。

题目已知甲和乙的具体效率，甲制作杯身和杯盖的效率均比乙大，但是这两部分都需要有人做，那么我们就要让相对效率更高的人做适合的工作。对甲而言，制作杯身、杯盖两个部件的效率比为150：75=2：1；对乙而言，制作这两个部件的效率比为60：24=5：2，前者小于后者，因此乙更擅长制作杯身，则甲先进行杯盖的制作工作，若十天只进行各自工作，那么甲完成杯盖75×10=750个，乙完成杯身60×10=600个，则有150个杯盖会浪费，为让整体的数量再增加，甲除完成乙所需要的杯盖数量后，剩下的时间可进行整个杯子的制作。所以甲做600个杯盖需要600÷75=8天时间，那么剩余两天时间甲要做相同数量的杯身和杯盖自行匹配完整的杯子，根据效率之比2：1可知数量相同的情况下所用时间之比为1：2，即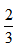天做杯身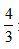，天做杯盖，则最后两天甲可完成杯子为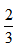×150=100个，总共可完成杯子600+100=700个。故选择C选项。

(二)已知每人完成各项工作的时间

例2：有甲、乙两个工程队负责某小区主干道维修及墙面粉刷。主干道维修，若两个工程队合作，30天完成，若乙工程队单独进行，105天完成；粉刷墙面，若两个工程队合作，28天完成，若甲工程队单独做，140天完成。如果两项工作两个工程队共同合作，最少需要多少天？（）

A.34 B.35 C.40 D.41

【答案】C【解析】设主干道维修的工程量为30和105的最小公倍数210，则甲、乙合作修主干道的效率和为210÷30=7，乙的效率210÷105=2，那么甲的效率为7-2=5；

设粉刷墙面的工程量为28和140的最小公倍数140，则甲、乙合作刷墙面的效率和为140÷28=5，甲的效率为140÷140=1，那么乙的效率为5-1=4。

两个工程队合作完成时间最少，则优先让两个工程队独自完成自己效率较高的工作，甲完成这两个工作效率之比5：1，乙为2：4，前者大于后者。因此甲相对更擅长修主干道；乙相对更擅长粉刷墙面。再让先完成的一方帮助另一方，从而完成全部工作。

甲单独修完主干道需要210÷5=42天，多于乙单独完成墙面粉刷时间140÷4=35天，因此乙完成墙面粉刷后与甲完成主干道维修工作。此时甲已完成主干道维修的工作量为35×5=175，剩余210-175=35，由甲、乙一起完成，需要35÷7=5天，总时间需要35+5=40天。故选择C选项。

总结：题干中已知效率时，当甲完成A产品与B产品的效率之比大于乙时，则甲相对擅长做A产品，乙相对擅长做B产品，再具体根据题目所给数据进行统筹分工；题干中已知时间时，我们也可以根据时间求出效率通过比较后进行统筹分工。

政华公考相信大家通过上述题目，能对多劳力问题有一定的了解，大家在备考期间需多多练习总结，掌握这类问题。

行测数量关系工程问题中的特值法

行测数量关系工程问题中的基本公式大家已经非常熟悉：工作总量=工作效率×工作时间。而在实际考试当中，工程问题多数情况会考查多者合作，就稍显复杂了，那多者合作问题该如何解题呢？须知世异则事异，事异则备变，今天政华公考带大家一起来了解如何利用特值法让多者合作问题变简单！

多者合作研究的是多个主体通过一定方式合作完成工作的问题，合作效率等于各个主体的效率加和。解决多者合作问题，可适当结合题干信息将未知量设为特值，来简化运算。

一、已知多个主体完工时间，可设工作总量为1或完工时间的最小公倍数为特殊值

例1：某水池装有甲、乙、丙三根注水管，单独开甲管10分钟可将水注满，单独开乙管15分钟可将水注满，单独开丙管6分钟可将水注满，那么三管齐开需要多少分钟可以将水注满？（）

A.5 B.4 C.3 D.2

【答案】C【解析】所求为三管齐开的时间，根据工程问题基本公式，需要用工作总量除以三个管的效率加和。题干给出了甲乙丙各自将水注满的时间，因此可设工作总量为特值。

方法一：设工作总量为1，甲的效率即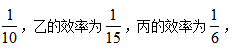为所求时间为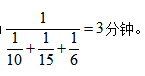故选C项。

方法二中三人的效率可直接表示为整数，明显计算更加简单，因此可以考虑直接设工作总量为时间的最小公倍数，以简化运算过程。

二、已知多个主体效率的比例关系时，一般根据效率关系将效率最简比设为特值

例2：甲、乙、丙三队合作修马路，已知甲队每天修的路程是丙队的3倍，乙队每天修的路程是丙队的2倍，三队合作6天完成总路程的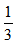后，甲休息6天后接着干，乙休息9天后接着干，丙不休息一直干，最终完工。则开始到完工需要多少天？（）

A.24 B.28 C.32 D.36

【答案】A【解析】根据题意可知“甲的效率是丙的3倍，乙的效率是丙的2倍”，可知甲、乙、丙三者效率的比例关系为3：2：1，设丙的效率为1，则乙的效率为2，甲的效率为3；三队6天完成总路程的，则剩余部分按原效率需12天完成，剩余工作量为(3+2+1)×12，设剩余工作还需时间为t，根据甲乙丙三人的工作量加和等于剩余工作量，可列方程3×(t-6)+2×(t-9)+1×t=(3+2+1)×12，解得t=18，共用时间6+18=24天。故选A项。

通过政华公考上述两个例子可以发现，使用特值法解决多者合作问题可以简化运算，一般可再结合工作总量列方程求解。百尺竿头须进步，希望同学们不要疏于练习，博观而约取，厚积而薄发！