政华教育

在例题中，5次射击有4次命中10环，首先需要从5次里任意选择4次命中10环，顺序对结果没有影响，所以为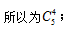每次射击命中10环的概率为0.8，每次射击是否命中互不影响，因此命中4次10环的概率为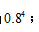总共5次，命中4次10环，还有1次不是10环，概率为1-0.8=0.2，共1次，概率为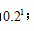必须完成5次射击，则上述过程为分步过程，最终结果为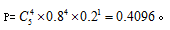

公式总结：某试验独立重复n次，其中A事件要么发生，要么不发生，且A事件每一次发生的概率均为p，则在n次试验中A事件发生k次的概率为：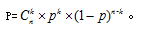

例题精讲

例1：植树节期间，某单位购进一批树苗，在林场工人的指导下组织员工植树造林。假设树苗的成活率为50%，那么，该单位职工小张种植5棵树苗，至少成活4棵的概率是多少？（）

【答案】C【解析】每棵树是否成活互不影响，且只有成活和不成活两种情况，每棵树木成活概率均为50%，符合多次独立重复试验模型，事件A为树木成活。5棵树至少成活4棵可以分为两种情况：

例2：某次乒乓球比赛中采取五局三胜，小王和小张进行一场比赛，比赛中小王每一局比赛获胜的概率均为0.6，则小王在这次比赛中最终获胜的概率约是多少？（）

A.30%—40% B.40%—50% C.50%—60% D.60%—70%

【答案】D【解析】每局比赛是否获胜互不影响，且只有获胜和不获胜两种情况，每局获胜概率均为0.6，符合多次独立重复试验模型，事件A为小王获胜。由于比赛的特殊性，小王在获取三局胜利后比赛结束，故最后一局必然为小王获胜。最终小王获胜可分成三种情况：

因为共分了3类，为分类过程，则小王获胜的概率为21.6%+25.92%+20.736%=68.256%，故本题选择D。

通过上述讲解，大家对于多次独立重复试验公式的应用环境有所了解，但一定要注意分局比赛时的决胜局，政华公考建议大家在备考期间多多练习，做到真正熟练掌握此类题目。

行测概率问题如何不再靠“概率”

目前来说，行测考试中的数量关系成为众多考生不得不做的一个部分，放弃这部分往往也意味着放弃了高分。数量关系作为行测考试中较难的部分，想要在较短时间内做出来，还是需要考生掌握一定的做题技巧。下面，政华公考带大家一起学习一下行测考试中高频考点之一——概率问题的做题技巧。

例题展示：某单位的会议室有5排共40个座位，每排座位数相同。小张、小李随机入座，则他们坐在同一排的概率：（）

A.不高于15% B.高于15%但低于20%

C.正好为20% D.高于20%

此题我们将从常规解法和技巧类解法给大家进行求解展示：

常规解法

概率的基本求解公式如下，

因此此题只需要求出所求事件以及总事件的样本数即可。

例题：5排共40个座位，每排的座位数相同，则每排有8个座位。总事件是从40个座位中选择2个座位给小张、小李，所求事件是小张、小李坐在同一排，可以从先选择一排，再从这排中选择2个座位给小张、小李，分步相乘，选择B选项。

总结：遇到概率问题需先找到总事件和所求事件，再求出总事件的等可能样本数，以及满足问题中具有限制条件的等可能样本数，进而直接利用公式解题。如果所要计算的样本数相对复杂时，一般可借助排列数和组合数对样本数进行求解。

技巧类解法

例题：5排共40个座位，每排的座位数相同，则每排有8个座位。假设小张已经选好座位，即小张固定了座位，此时还剩下39个座位，小李要想同小张坐在同一排，小李只能从小张所在排剩余7个座位中选一个，故小张、小李在同一排的概率为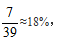选择B选项。

总结：在概率问题中，当遇到要同时考虑相互联系的元素时，可以先将其中一个固定，再考虑其他元素的所有可能情况，从而进行求解。

通过比较发现，显然技巧类解法更加便捷快速，该技巧解法为定位法，在近几年行测考试中应用较多，希望大家能够掌握并灵活使用。接下来通过下面这道题目，来练习使用定位法求解概率。

例题：胜利小学的225名同学与红旗小学的256名同学一起春游，将两所小学的同学混合在一起，随机组合，重新组织队伍，要求每队人数相同且队伍数尽可能少。那么胜利小学的张华与红旗小学的张明出现在同一队伍的概率为：（）

A.5.5% B.6.5% C.7.5% D.8.5%

【答案】C【解析】参加春游的学生共有225+256=481名。481=13×37，要求每队人数相同且队伍数尽可能少，则每队有37人，共有13队。张华和张明存在相互联系，假设张华已经选好了队伍，此时剩下480个位置，张明要想和张华在同一队，只能从张华所选队剩余36个位置选一个，故所求概率为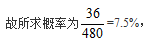选择C选项。

任何方法的灵活掌握都不是一蹴而就的，因此在解决概率问题时，大家遇到“要同时考虑相互联系的元素时”，要考虑使用定位法，通过大量练习，能够熟练使用，且做到举一反三，这样在考试中遇到便能快速解题，为顺利进入面试多一份助力。

行测数量关系：定位法解决概率问题

在近几年的行测考试当中，古典概率问题常常出现。对于部分古典概率题目来说，除了可以运用公式求解之外，还可以利用定位法求解。接下来政华公考就为大家介绍如何利用定位法求解部分概率问题。

定位法适用条件

1.古典概率问题中，遇到要同时考虑相互联系的元素。

2.无论第一个元素选哪个位置，都不影响之后选择的可能性。

定位法具体步骤

先将其中一个元素固定，再考虑其他元素的所有可能情况，从而求解。

经典例题

例1：从3双完全相同的鞋中，随机抽取一双鞋的概率是：( )。

【答案】B【解析】方法一：A事件发生的概率等于A事件包含的等可能样本数除以总的等可能样本数。总的事件是随机从6只相同的鞋中抽取两只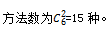，A事件是抽取一只左侧、一只右侧鞋子的方法数为因此，选择B选项。

以上是这道题的常规破解思路，那么接下来让我们看一下如何利用定位法解决这道题目。

方法二：想要抽取一双鞋，我们可以考虑一只一只地取，无论先选左脚还是右脚，都不影响最终结果。我们可以先固定一只，比如先随便抽取一只，如果是左脚，那么剩下的5只鞋中，有3只右脚能与之配对成一双鞋，所以随机抽取一双鞋的概率为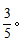因此，选择B选项。

例2：某学校组织迎新篝火晚会，100名新生随机围坐在篝火四周。其中，小张与小李是同桌，他俩坐在一起的概率为( )？

【答案】C【解析】要求小张与小李挨着坐，先选谁、后选谁都不影响最终结果。若小张固定了座位，剩下还有99个座位可供小李选择，其中左右两侧都跟小张挨着。所以，有2个座位符合要求，故两人挨着坐的概率为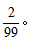

政华公考相信通过上述题目的练习，大家对于定位法已经有所了解。以后当在古典概率问题中遇到要同时考虑相互联系的元素，并且无论第一个元素选哪个位置，都不影响之后选择的可能性时可先将其中一个元素固定，再考虑其他元素的所有可能情况。希望大家在之后的学习当中，能够真正利用定位法解决概率问题。加油！