行测数量关系指导：妙用方法，巧解等差数列
妙用“中项”，巧解等差数列
在行测数量关系中，等差数列作为常见考点，相信大家对它都不陌生了。等差数列中经常用到求和公式，在我们利用高斯求和公式解题的时候会发现，它往往还需要结合通项公式，计算过程相对比较复杂，今天政华公考就带大家来学习一下中项求和公式，让同学们在考场上能够快速解决等差数列问题。
一、等差数列中的常用求和公式
1.高斯求和公式
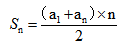
2.中项求和公式
二、例题运用
例1：某个阶梯教室有25排座位，后一排均比前一排多两个座位，已知第13排有56个座位，问这个教室一共有多少个座位?（ ）
A.1200 B.1400 C.1600 D.1800
【答案】B【解析】题中“后一排比前一排多两个座位”，也就是告诉我们这个教室
总结：当项数为奇数时，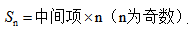
，此时中间项只有一项，为第
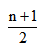项。
例2：某单位进行技能测试，10名工人的成绩恰好构成等差数列，从高到低，后面一人分数总是比前一人少4分，如果从高到低排名第5的工人分数为80，那这10人的总分数是多少?（ ）
A.560 B.680 C.780 D.860
【答案】C【解析】由题可得，工人的分数从高到低构成了一个公差为-4，项数为10的等差数列，当项数为偶数时，我们可以用中间两项和替代首项加末项，中间两项即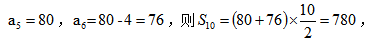
故选择C项。
总结：当项数为偶数时，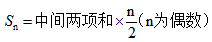
，此时中间项有两项，为
在上述例题中，通过对“中项”的巧用，帮助我们快速准确地选出了答案，所以大家在做等差数列的题目时，可以根据题目条件灵活选择高斯求和公式或中项求和公式，希望今天的分享能够为大家的备考起到助力作用。
面对等差数列该怎么“抉择”
说起行测中的等差数列，可能大家能立马想到通项公式和求和公式，但是具体的公式却又记不住了，这就导致连最基本的题目都无法求解，所以记住公式是第一步，能记住，更重要的是要学会灵活运用。考试中一般以求和为主，如何根据题干，选择准确的求和公式，才能高效解题，事半功倍。今天政华公考就跟大家一起来回顾一下公式，然后去推导公式，帮助大家更好的解题。
基本公式
公式推导
公式选用的依据
实战演练
例1：某商店10月1日开业后，每天的营业额均以100元的速度上涨，已知该月15日这一天的营业额为5000元，问该商店10月份的总营业额为多少元?（ ）
A.163100 B.158100 C.155000 D.150000
【答案】B【解析】题目中出现每天的营业额均以100元的速度上涨，则每天的营业额构成以100为公差等差数列，10月共有31天，即所求为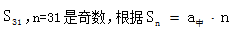
(当n为奇数时)求解，16日的营业额为中项，依题意16日营业额为5000+100=5100元，
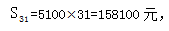选B。
例2：某水产养殖场养殖一种石斑鱼，该鱼种成熟期是三年，其后便可销售。已知该渔场从2010年3月开始投放2000尾鱼苗，之后每年3月比上一年多投放200尾鱼苗，若投放后鱼苗均能成活，且所有成熟的鱼均销售一空，那么该渔场到2017年5月底共有( )条石斑鱼。
A.8000 B.8400 C.9600 D.10800
【答案】C【解析】根据题意可知，自2010年3月起，每年3月投放的鱼苗数构成了首项为2000、公差为200的等差数列。因鱼种成熟期是三年，且所有成熟的鱼均销售一空，则2017年5月月底，渔场中还剩下2015年3月-2017年3月投放的石斑鱼，这三年投放的鱼苗中2016年投放的尾数为中项。则2016年3月投放的鱼苗数可根据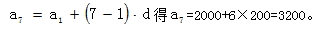
因为2015、2016、2017这三年投放的鱼苗数构成等差数列，求这三年的共投放的鱼苗数，
即到2017年5月底渔场中共有9600条石斑鱼，选C。
上述两个例子都是求和公式，这个就需要同学们能够根据题干找准求和公式，再结合推导公式求出所需要的项，这样解题才会能减少不必要计算，高效解题，同时希望大家要多加练习，背熟公式，这样在做题时才会更加熟练。
等差数列之中项法求和的妙用
等差数列，顾名思义，指的是从第二项起后一项与前一项作差得到一个相同常数的数列。近三年国考行测每年都会考查等差数列，其重要性不言而喻。这类题难度不大，只要了解一些基本概念
掌握一些核心的计算关系，题目都可以轻松求解。政华公考在此进行展开分析。
公式是解题的核心，需牢记
1.通项公式
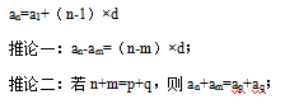
2.求和公式
其中利用中项求和是考试重点，且应用起来非常方便，接下来我们通过几道题目来感受一下。
提炼概念，套用公式
例1：
【答案】195【解析】这道题要求的是前13项和S3。如果利用基本的求和公式，需要知
例2：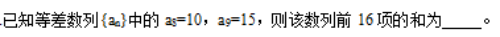
【答案】200【解析】该题目求解的是前16项的和S6，如果利用基本求和公式，需要知
例3：某商店10月1日开业后，每天的营业额均以100元的速度上涨，已知该月15日这一天的营业额为5000元，问该商店10月份的总营业额为多少元?（ ）
A.163100 B.158100 C.155000 D.150000
【答案】B【解析】根据题干条件“每天的营业额均以100元的速度上涨"可知，每天的
通过这三个例题可以发现在遇到等差数列求和时，利用中项法求和公式来计算会比直接利用基本公式更简单一些，那么做题的时间也会相对减少，效率提升，大家赶紧练起来吧!
