行测数量关系：利润问题这样解更速度
行测“钱多多”之巧解利润问题
“明日复明日，明日何其多。我生待明日，万事成蹉跎。”行测备考不容拖沓，利润问题又是行测考试中的高频考点，如何更顺利解决利润问题，接下来政华公考带领大家进入到利润问题的学习中！
基本计算关系式
解题方法
1.如果题干描述的量比较单一，可直接利用利润问题的基本公式进行求解。
例1：某早餐店试营业主打套餐每份成本8元，售价26元。当天卖不完的主打套餐不再出售，在过去两天时间里，餐厅每天都会准备200份主打套餐，第一天剩余20份主打套餐，第二天全部卖光。问这两天该早餐店主打套餐共盈余多少元？（ ）
A.6680 B.6840 C.7000 D.7160
【答案】A【解析】这两天早餐店的总成本是200×2×8=3200元，总售价是(200×2-20)×26=9880元，则这两天该早餐店主打套餐共盈余9880-3200=6680元。故本题选A。
2.如果题干描述的量比较多，可通过列表梳理各个量之间的联系，再建立等量关系求解。
例2：某家具店购进一批桌椅，每套进价200元，按期望获利50%定价出售。卖掉这批桌椅的60%以后，店主为提前收回资金，打折出售余下的桌椅。售完全部桌椅后，实际利润比期望利润低了18%。问：余下的桌椅是打几折出售的？（ ）
A.七五折 B.八二折 C.八五折 D.九五折
【答案】C【解析】设总销量为m件，打了10n折。
期望总利润为100m元，实际利润为100m×(1-18%)=82m元，故60m+(300n-200)×0.4m=82m元，方程左右两边可约去m，解得n=0.85，即余下的桌椅是打八五折出售的。故选C。
通过计算不难发现，等号左右两边的销量m可约掉，因此销量m的取值对最终结果无影响，故在进行求解时同学们也可直接将销量设为特值。
政华公考相信同学们对于利润问题求解有了进一步的了解，希望大家接下来多加练习，考试再难也不怕，撸起袖子加油干！
两数之积的增长率在行测利润问题中的应用
同学们做行测题目时常常会遇到利润问题，这个知识点难度不大关键在于方法的选择。今天政华公考给大家分享利润问题中如何利用两数之积的增长率公式快速解题。
例1：某钢铁厂生产一种特种钢材，由于原材料价格上涨，今年这种特种钢材的成本比去年上升了20%。为了推销该种钢材，钢铁厂仍然以去年的价格出售，这种钢材每吨的盈利下降40%，不过销售量比去年增加了80%，那么今年生产该种钢材的总盈利比去年增加了多少？( )
A.4% B.8% C.20% D.54%
【答案】B【解析】方法一，分析题干，钢材的总盈利=钢材的每吨盈利×钢铁的销售量。设去年的每吨盈利为x，销量为y，可得总盈利为xy；则今年每吨盈利为x(1-40%)=0.6x，销量为y(1+80%)=1.8y，可得总盈利为0.6x×1.8y=1.08xy。故今年生产该种钢材的总盈利比去年增加了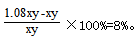
故选B项。
由方法一我们不难看出，此题可以用方程法来进行求解，但是由于未知数比较多，同学们计算的时候也会更加复杂。今天政华公考给大家总结规律，帮助大家更快速求解题目。
例2：有一本畅销书，今年每册书的成本比去年增加了10%，因此每册书的利润下降了20%，但是今年的销量比去年增加了70%。则今年销售该畅销书的总利润比去年增加了：( )。
A.36% B.25% C.20% D.15%
【答案】A【解析】题目当中畅销书的总利润=每册书的利润×销量，即出现
通过上面两个例题，大家会发现若掌握两数之积的增长率公式可以快速解决利润问题。你还能想到哪些概念可以用此方法吗？
一元二次函数在行测利润题目中的应用
利润问题是行测考试中的常考题型，其中求利润或收入最大值的题目出现频率较高，这类题利润=单价×销量，单价以及销量都在变，概念多且变化让同学头疼不已，其实这类题就是纸老虎，看着难，一学都觉得简单。今天政华公考就带着大家学习一下利用极值思想求解的利润问题，我们先来看一道例题：
例1：某商店购进一批单价为20元的日用品，如果以单价30元销售，那么半个月内可以售出400件。根据销售经验，提高单价会导致销售量的减少，即销售单价每提高1元，销售量相应减少20件。将售价定为多少元，才能在半个月内获得最大利润？（ ）
A.34 B.35 C.36 D.37
【答案】B【解析】根据题意，每次涨价，销量就会随之下降，要求的是最大利润，而总利润=单件利润×销量，因此总利润会随着单件利润和销量的变化而变化。
按原价出售单件利润为30-20=10元，半个月可以销售400件，而此时每涨价1元就会少卖20件，我们不妨设涨价x元，销量对应为(400-20x)件，那么可以得到总利润=(10+x)×(400-20x)，即为一个一元二次方程，怎么求最值呢？可以借助函数图像来理解：
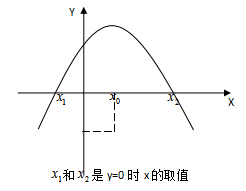
其函数图像为一个抛物线。我们要求最大总利润，即抛物线对称轴的对应点。此时令总利润为0，可得抛物线与x轴上的两个交点，即10+x=0或400-20x=0，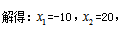
而抛物线对称轴即为与x轴两个交点的中间值。
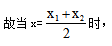总利润有最大值，
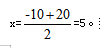那么应涨价5元，售价定为30+5=35元，选择B选项。
例2：某大型批发超市销售某种零食，平均每天可售出20箱，每箱收入40元.为了扩大销售、增加收入，该店采取了降价措施，经过一段时间销售，发现销售单价每降低2元，平均每天可多售出5箱.问每箱商品降价多少元时每天所得收入最大？（ ）
A.14 B.15 C.16 D.17
【答案】C【解析】由题意每降价2元就会多卖5箱，如果我们设降价x元，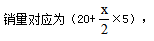
可以看出，这样的设法增加了表示销量的难度，且存在分数也加大了计算的难度。既然每降1个2元可多售出5箱，那不妨设降了x个2元，则可以多卖5x箱，总收入=(40-2x)×(20+5x)，与例1相同，我们要求最大总收入，此时可令总收入为0，那么可得40-2x=0或20+5x=0，
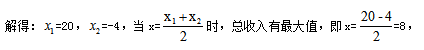那么应降价8个2元即降价16元，故选择C选项。
总结：通过上述两道例题，可以得出三点解题思路：
1.若题目表述为“每提(降)价n元，销量减少(增加)m件”，则设提(降)价x个n元；
2.利用基本公式“总利润(总收入)=单个利润(单个收入)×销量”构造等量关系；
3.令总收入/总利润为0，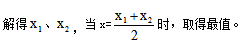
政华公考希望同学们通过学习能够在行测考试中灵活运用思路快速解题。
均值不等式巧解利润最值问题
利润问题是行测考试中数量关系部分的一种题型，这种题型中有一类考点，即求利润的最值，此类题目在求解过程中往往会出现一元二次函数，如何简便快速地求解一元二次函数的极值，下面就为大家介绍一种方法，即利用均值不等式来求解。
均值不等式的一种表达形式如下，
如果a、b均为非负实数，那么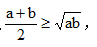
当且仅当a=b时，等号成立。
由上述表达式，我们可以得到如下结论：已知a、b均为正数，若a+b为定值，则当且仅当a=b时，ab取得最大值。
示例：已知x>0，y>0，且2x+5y=20，则xy的最大值是多少？
在这道题目中，2x相当于a，5y相当于b，则a+b=20，是定值，所以当且仅当a=b，即2x=5y时，2x×5y存在最大值，因为2x=5y且加和等于20，所以2x=5y=10，求出2x×5y=10xy=100，即xy最大值为10。
应用
例1：某商场销售一批名牌衬衫平均每天可售出20件，每件盈利40元。为了扩大销售增加盈利尽快减少库存，商场决定采取适当的降价措施，经调查发现如果每件衬衫每降价1元，商场平均每天可多售出2件，每件衬衫降低( )元时，商场每天盈利最多。
A.12 B.15 C.20 D.25
【答案】B【解析】接下来通过本题的解析我们梳理此类题目的解题思路：
(1)找等量关系，列方程。
本题所求为利润最值问题，结合条件可以得出等量关系：总利润=单件利润×销量。分析可得如果售价下降1元在成本不变的情况下利润即下降1元，同时销量会增加2件，这道题可以设每件衬衫的售价下降了x元，商场的总利润为y元，那么可列出方程y=(40-x)×(20+2x)。
(2)凑配定和，求极值。
y=(40-x)×(20+2x)，由前面学习的均值不等式的结论可知，要想求两部分乘积的最大值，需要这两部分的加和为定值，而我们会发现40-x和20+2x的加和并不是常数，所以不为定值，那么就需要未知数在加和后抵消掉，则可将方程变形为y=2×(40-x)×(10+x)，此时40-x与10+x的和为定值，所以当且仅当40-x=10+x，即x=15时，y存在最大值，答案为B。
例2：某宾馆有50个房间供游客居住，当每个房间定价为每天180元时，房间会全部住满，当每个房间的定价每增加10元时，就会有一个房间空闲，问房价为多少元时宾馆利润最大？（ ）
A.260 B.280 C.300 D.340
【答案】D【解析】总收入最多则利润最大，所以需要求出总收入的最大值，通过题干条件可得等量关系为：总收入=房间单价×入住房间数量，房价增加会使入住房间数减少，此时可设房价增加了x个10元，总收入为y元，可得y=(180+10x)×(50-x)，想求两个部分乘积的最大值，需要使两部分加和为定值，可将方程变形为y=10×(18+x)×(50-x)，当且仅当18+x=50-x，即x=16时，y取最大值，此时每个房间的价格为180+10×16=340元，故答案为D。
通过上述例题我们可以发现，利润最值问题采用均值不等式的思想来求解是非常简单的，希望同学们能够多看几遍，充分吸收，做到熟能生巧、举一反三。
