政华教育

【答案】B【解析】由题干可知4个小朋友分25个草莓，4个人分的草莓总数为定值。所求为分得最多的一个小朋友最多分得多少个，即求最大量的最大值，符合和定最值的题型特征。根据解题思路“和一定，求某个量最大值，其余量尽可能小”，可确定分得的草莓数最少的小朋友分1个，又因题干要求每人分到草莓且数量不同，则所分草莓数分别为：

所求为25-3-2-1=19，故选C。

小结：根据解题原则确定其他量具体的数值，利用几个量的和为定值即可解题。

例2：学校将33个篮球分给6名同学，且分得的数量不同，问分得篮球最多的同学，至少分得多少个？（）

A.6 B.7 C.8 D.9

【答案】C【解析】根据解题思路“和一定，求某个量最小，其余量尽可能大”，可设分得篮球最多的小朋友至少分x个，又因题干要求每人分到的篮球数量不同，则所分篮球数分别为：

列式为6x-15=33，x=8，故选C。

例3：贸易公司有三个销售部门，全年分别销售某种重型机械38台，47台，35台，问该公司当年销售该重型机械数量最多的月份，至少卖出了多少台？（）

A.10 B.11 C.12 D.13

【答案】A【解析】由题意可知全年销售总量为38+47+35=120台，和一定，并且所求为销售最多的月份销售量的最小值。根据解题思路“求某个量最小值，其余量尽可能大”，故将销售最多的月份销售量设为x。又因题干没有要求每个月份销售量不同，销售第二多的月份销售量尽可能大，最大也为x，以此类推，则每月销售量分别为：

列式：12x=120，x=10台，故选A。

小结：根据解题原则不能直接确定其他量具体的数值，可假设所求量为x，其他量由x进行表示，再利用几个量的和为定值解题。

例4：从某物流园区开出6辆货车，这6辆货车的平均装载量为62吨，已知每辆货车装载量各不相同且均为整数，最重的装载了70吨，最轻的装载了54吨。问:这6辆货车中装货第三重的货车至少装载了多少吨？（）

A.59 B.61 C.62 D.63

【答案】C【解析】根据“这6辆货车的平均装载量为62吨”可得6辆货车总装载量为62×6=372吨。根据解题思路“和一定，求某个量最小，其余量尽可能大”，可确定第一重的装载70吨，第二重的装载69吨，所求的第三重的装载x吨，第四重的尽量重但不超过第三重的，所以为x-1吨，同理第五重的为x-2吨，第六重的根据已知条件为54吨，分别表示如下：

列式：70+69+x+(x-1)+(x-2)+54=372，x≈60.7，为最小值，即最小不能小于60.7，但题目要求装载量为整数，所以向上取整为61，选B。

小结：和定最值问题在解方程的过程中最后的结果可能会存在小数，要结合题目所求进行向上或向下取整：

(1)题目求最大值，向下取整。

(2)题目求最小值，向上取整。

根据上述的学习，我们已经基本掌握了和定最值的做题方法：(1)判断题型，(2)根据和定最值原理解题。不过在解题的过程中要注意：(1)题干已知条件中是否有各不相同；(2)最后的计算结果不是整数时如何进行取整。掌握做题方法的同时注意细节，考试时定能拿下这种题型的分数。

行测利润问题之常用公式的使用

利润问题是数量关系中的常考题型，在行测考试中，利润问题常涉及成本、售价、利润、利润率、打折率等概念。其实考试就考查这些概念之间的关系即基本公式，大家学会这些公式，就可以高效地解决利润问题。

常考的利润问题基本公式有以下5个：

下面我们通过题目来学习如何利用这些基本公式解题。

例1：某商场柜台销售一款时装，若将进价的20%作为利润，则销售价为240元。若该款时装销售价为300元，此时利润率是：（）

A.50% B.45% C.40% D.35%

【答案】A【解析】问题问的是当售价为300元时的利润率，而成本是不会变的，且题干已经知道了当售价为240元，利润率为20%，所以根据公式成本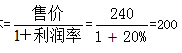所以当售价为300时，所以此题选择A。

例2：某服装店从韩国代购100件羽绒服，每件进价300元，另外还需要付10元/件的代购费和200元的国际快递费。该服装店要想每件羽绒服获得75%的利润率，则每件定价为多少元，如果在此基础上打九折，此时的利润为多少元/件？（）

A.546，491.4 B.564，179.4

C.546，179.4 D.564，491.4

【答案】C【解析】问题想要求的这件衣服的定价，而由题干可得每件羽绒服实际总成本包括每件羽绒服的进价、代购费和快递费，这里需要注意的是进价和代购费都是单件的，而快递费是100件的，所以总成本应为300+10+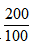=312元，根据公式定价=成本×(1+利润率)=312×(1+75%)=546元。排除B，D两个选项，而第二问的是要在此定价的基础上打九折时求利润，根据打几折=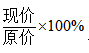能得到现价=原价×打几折=546×0.9=491.4元，而成本是不变的所以根据利润=售价-成本=491.4-312=179.4元，所以此题选择C选项。

例3：某种汉堡包每个成本4.5元，售价10.5元。当天卖不完的汉堡包即不再出售。在过去十天里，餐厅每天都会准备200个汉堡包，其中有六天正好卖完，四天各剩余25个。问这十天该餐厅卖汉堡包共赚了多少元？（）

A.10850 B.10950 C.11050 D.11350

【答案】B【解析】题干求的是十天共赚了多少钱，求的是总利润，根据公式利润=售价-成本，所以只需求出总售价和总成本即可，而总售价=单售价×数量，十天中有六天刚好卖完，有四天各剩25个，所以一共卖出去了6×200+4×(200-25)=1900个，所以总售价为1900×10.5=19950元，而总成本=数量×单成本，这里需要注意，虽然有四天没卖完，但是已经做了，成本就必须算进去，所以总成本=10×200×4.5=9000元，最终总利润=19950-9000=10950元，此题选择B。

以发现，在利润问题中，只要牢牢掌握基本公式，那么再难的利润问题也可以迎刃而解，希望大家勤加练习，彻底攻克利润问题，以便在考试中夺得先机。

行测数量关系：遇到星期、日期问题这么办

在行测考试中，数量关系是其中重要的一个部分，但由于时间和速度关系，数量就没时间做让人头疼不已。不过，一些简单的数学运算题我们不必轻言放弃，例如数量关系中偶尔会考察到的星期、日期问题，大家可以尝试着学习之后快速突破。

一、星期、日期常识

星期、日期问题在数量关系里相对来说属于比较简单的一类题型，解决这类题型需要我们知道一些关于星期、日期的基本知识。

1.平年、闰年

(1)平年365天，闰年366天

(2)平年、闰年判定

①公元年数非100倍数的年份：能被4整除的是闰年，其余则为平年(如2020年是闰年)；

②公元年数是100倍数的年份：能被400整除的是闰年，其余则为平年(如2000年是闰年，1900年是平年)

2.大月、小月

大月(31天)：1、3、5、7、8、10、12月

小月(30天)：4、6、9、11月

平年2月有28天，闰年2月有29天。

3.星期

周一到周日循环，其本质上就是余数问题，星期几就是除以7余几。平年365天除以7是52周余1天；闰年366天除以7是52周余2天。

二、常见考法

1.根据已知年月日求星期几

例1：2020年7月1日是星期四，那么2021年12月10日是星期几？（）

A.星期二 B.星期三 C.星期四 D.星期五

【答案】D【解析】由题意可知，从2021年7月1日到2021年12月10日，还需经过7月份剩下的30天、8月份31天、9月份30天、10月份31天、11月份30天、12月份10天，共计162天。一周为7天，以7天为一个周期，则162÷7=23……1，经过了23周余1天，故2021年12月10日是星期四的后一天，即星期五。故本题选D。

2.已知某月星期数量，求具体星期几

例2：姐姐问弟弟一个问题，某年2月有5个星期三，则当年7月1日为星期几？（）

A.星期六 B.星期日 C.星期五 D.星期四

【答案】B【解析】平年2月有28天，闰年2月有29天。题目中给出2月有5个星期三，那么该年2月有4个完整的星期外加一天。则该年2月有4×7+1=29天，为闰年。而且多出来的一天为星期三，即2月29日为星期三。2月29日到7月1日经过31+30+31+30+1=123天，123÷7=17……4，则7月1日为星期日。故本题选B。

3.已知间隔时间，求下一次相遇

例3：甲、乙、丙三人均每隔一定时间去一次健身房锻炼。甲每隔2天去一次，乙每隔4天去一次，丙每7天去一次。4月10日三人相遇，下一次相遇是哪天？（）

A.5月28日 B.6月5日 C.7月24日 D.7月25日

【答案】C【解析】根据题意可知，甲每3天(每隔2天)、乙每5天(每隔4天)、丙每7天去一次健身房，则三人再次相遇需105天(3、5、7的最小公倍数)，4月剩20天，5月31天，6月有30天，105-20-31-30=24天，则下次相遇在7月24日。故本题选C。

通过以上三道例题的学习，相信我们对日期、星期问题有了基本的了解和学习，再多加练习就可以对此类题型牢牢掌握了。

行测数量关系：虚张声势的不定方程，你被吓到了吗？

行测考试中哪个部分题目最有挑战性？非数量关系莫属了。很多考生一看数量就萌生了“数量关系全放弃，提笔就蒙C和B”的想法。然而，如果想取得好成绩，数量关系无疑是拉开分距的重要部分，全放弃显然是不行的，所以需要我们去找到一部分简单的或者看似复杂但是通过简单学习能够拿分的题目，今天政华公考就说其中一种虚张声势的题型——不定方程。

一、认识不定方程

我们通过一个例题来认识一下何为不定方程：

例题：某单位根据人数给各部门发放中秋节礼品，后勤部每个工作组发放7份礼品，销售部每个工作组发放3份礼品，两个部门共发放33盒礼品。问该单位后勤部有多少个工作组？（）

A.2 B.3 C.4 D.6

【政华思路】我们发现，这样的题目能够很容易找到等量关系并列出方程：设后勤部x个工作组，销售部有y个工作组，列出方程为：7x+3y=33。但是我们观察这个方程不难发现，它有两个未知数，也就是未知数的个数多于方程的个数，其实，这样的方程就叫做不定方程。

初学方程的时候未知数数量多于方程的数量，这个方程就有无数组解，无法解出具体值，所以很多考生会很疑惑这样的题目到底如何做出来呢？但其实在行测考试中，我们求解的未知量都是人或者物品的个数，即未知数都是在正整数的范围内求解，所以，在这样的限制条件下，再加上选项的加持下，不定方程是可解的。

二、不定方程的解法

不定方程求解的核心思想就是代入排除。根据方程的特点，确定未知数的取值范围，然后进行代入排除。常见的可以利用的特点有以下几点：

(一)整除法：其中一个未知数系数与常数存在大于1的公约数，可以考虑利用整除特性进行求解。

例题：例如刚刚的题目：某单位根据人数给各部门发放中秋节礼品，后勤部每个工作组发放7份礼品，销售部每个工作组发放3份礼品，两个部门共发放33盒礼品。问该单位后勤部有多少个工作组？（）

A.2 B.3 C.4 D.6

【答案】B【解析】选择根据题意设后勤部x个工作组，销售部有y个工作组，列出方程：7x+3y=33，未知数y的系数为3，与常数项33呈存在公约数3，而y为工作组数量，必然为正整数，所以3y为3的倍数，33也为3的倍数，所以7x必然为3的倍数，而7与3互质，所以x必然为3的倍数才能满足条件。看选项排除A、C两项，代入B选项，可求解y=4，符合题意。选择B项。验证D项，代入后y为负数不符合条件，排除。

(二)奇偶性：当未知数系数有一个为奇数时，可以根据各项之间的奇偶关系来判断未知数范围。

例题：码头有29箱货物运往仓库，大货车每车可以装7箱货物，中型货车每车可以装4箱货物，现要一次性将货物恰好运完，每车都装满，则需要大货车和中型货车各多少辆？（）

A.1、6 B、2、4 C、4、1 D、3、2

【答案】D【解析】根据题意设大货车有x辆，中型货车有y辆，则有7x+4y=29。在这个方程中，我们发现整除法不能用了，但是观察方程特征，4为偶数，所以4y为偶数，29为奇数，根据“偶数+奇数=奇数”，我们可以确定7x必然为奇数，只有当x为奇数时才能满足条件，排除B、C两项，代入A，7×1+4×6≠29。所以选择D项。我们也可以验证一下D项，7×3+4×2=29，符合条件。

(三)尾数法：当未知数系数有一个为5或者5的倍数时，可以利用尾数来确定未知数取值范围。

例题：某学校运动会开幕式，共有98人参加检阅，男生4人一排，女生5人一排，都恰好站成规则矩阵，问男女人数可能的情况有多少种？（）

A.4 B.5 C.6 D.8

【答案】B【解析】根据题意：设男生站x排，女生站y排，则有：4x+5y=98。其实这道题我们会发现可以运用奇偶性来进行判断，4x为偶数，98为偶数，所以5y必然为偶数，由此确定y为偶数，但是这样y需要尝试的数字很多，2、4、6、8……这样就比较麻烦，进一步观察方程我们发现，5y是5的倍数，又为偶数，所以尾数必然为0，而结果98的尾数为8，进而我们可以确定4x的尾数必然为8。所以x的取值可能为2、7、12、17……，这样就发现需要尝试的数字范围就小了很多，代入之后我们发现符合条件的有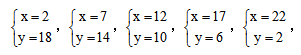：共有5组解，则男女人数也有5种情况，所以答案选择B选项。