行测数量关系常考题型快速解题技巧

行测数量关系快准狠题型之牛吃草

行测考试“时间紧，任务重”，数量关系对于很多同学来说确实是有难度的一部分，所以对于数量关系我们要智取，优先选择难度低用时短的题目，也要用合适的解题方法应对。其中行程问题让很多同学“闻风丧胆”，但是我们不要一棍子打死，里面的“牛吃草”问题就是一类在考试中易拿分的题型，并且思路固定，很好掌握。那今天政华公考就带领大家一起搞定“牛吃草”。

题型特征

1.出现时间的排比句式(如n头牛吃m天)

2.有一个初始量(操场的初始草量)受2个变量的影响(牛的数量、草长的速度)

例题1：牧场上有一片匀速生长的青草。这片青草供给10头牛吃，可以吃20天；供给16头牛吃，可以吃10天。则这片青草可供多少头牛吃6天？（   ）

A.21         B.22     C.23      D.24

思路点拨：1.题目中牧场上已经有一部分草量，在原有草量的基础上，牛一边吃，草一边长。草原上的草量受牛、草两个变量控制。2.题目中出现排比句式n头牛吃m天。

解题思路

1.追及型

上面的例题具体分析：牧场上原有一片青草，牧场可以是圆的，也可以是方的，但是不利于我们画图分析，我们不妨用一段线段来代表这片原有草量，牛在一端吃，草在另一端继续生长。当牛追上草的时候，不仅把原有草量吃完，并且把新生长的草也吃光了。这样就把这类题看成追及型问题。原有草量即为路程差用M来表示，一头牛的速度为1，n头牛的速度为n，设草的生长速度为x。利用路程差=速度差×时间来建立等量关系。即利用M=(n-x)×t列出连等式。

【答案】D【解析】设每头牛每天的吃草量为1，草匀速生长的速度为x，可供y头牛吃6天。根据题意有(10-x)×20=(16-x)×10=(y-x)×6，解得x=4，y=24。即可供24头牛吃6天。

例题2：某工地现有一定存量的砖，且每天供应量相等。若每天消耗27万块砖，则6天全部用完。若每天消耗24万砖，则9天全部用完。若每天消耗20万块砖，问：工地上的砖可以用多少天？（   ）

A.12       B.15      C.24     D.27

思路点拨：工地一定存量的砖即原有草量M。每天消耗砖相当于牛在吃，每天供应砖的量相当于草在长，且出现排比句式。代入公式列出连等式解题。

【答案】D【解析】设每天供应x万块砖，设所求为a天，则有6×(27-x)=9×(24-x)=a×(20-x)，解得x=18，a=27。故本题选D。

2.相遇型

例题3：由于气温升高，一个蓄水池的水量每天以均匀的速度减少，经计算，蓄水池的水供20户家庭用5天，或供16户家庭用6天，那么可供11户家庭用(   )天。

A.12       B.10        C.8      D.6

思路点拨：蓄水池原有水量相当于原有草量M，用一条线段表示，水量以均匀的速度减少相当于草在一端慢慢枯萎设为x，家庭用水相当于牛在一端吃，n户家庭设为n，当“草”和“牛”相遇即原有水量耗尽，此过程看做相遇问题，利用路程和=速度和×时间建立等量关系：M=(n-x)×t。

【答案】C【解析】设一户家庭1天的用水量为1，蓄水池的水量每天减少a，所求为x天，则有5×(20+a)=6×(16+a)=x×(11+a)，解得a=4，x=8。故本题选C。

综合看一下两种类型的题目的解题思路，不管是相遇型还是追及型，出现两个变量和排比句式时看做牛吃草问题，两种类型都是利用原有草量相等列连等式解题。只不过区别在于括号内是加法还是减法。我们可以这样理解当两个变量的目的相同时用加号，目的相反时用减号：例1牛在吃使原有草量减少，草在长使原有草量增加，目的相反，用减号；例2消耗砖使原有的砖减少，供应的砖使原有的砖在增加，目的相反，用减号；例3家庭用水使蓄水池原有水量减少，水量也以均匀的速度减少，目的相同用加号连接。这样牛吃草问题我们只要会判断题型，并且记住列连等式解题就可以轻松应对啦！

行测数量关系：巧用盈亏思想解题

盈亏思想是指多的量和少的量保持平衡的思想。在行测数量关系题目中，很多时候我们会利用等量关系解题，但有时解方程又会影响做题速度，若用盈亏思想去解题，可以简化计算的难度，提高做题效率。下面政华公考为大家带来盈亏思想在部分典型题目中的应用。

一、解题关键点

1.找准参照量作对比，比参照量多的部分叫做盈余，比参照量少的部分叫做亏损

2.盈余总量=亏损总量

3.盈余或亏损总量=每份盈亏量×份数

接下来我们来看看如何运用盈亏思想解题。

二、例题精讲

例题：随着全国各地疫情防控常态化，日常生活出行佩戴口罩已成为必要。某口罩加工厂计划每周生产A、B两个类型口罩共计9000个，其中A款防护口罩每个生产成本为1.6元，单个售价为2.3元；B款防护口罩每个成本为2元，售价为3元。现假设该加工厂每周生产这两种口罩的总成本不得高于15000元，则要使得口罩加工厂利润最大，加工厂每周需要生产A款口罩多少个？（   ）

A.0枚       B.6000枚    C.7500枚      D.9000枚

【答案】C【解析】由题意可知A款口罩单个利润为2.3-1.6=0.7元，B款口罩单个利润为3-2=1元，因此要想工厂利润最大应该优先多生产B款口罩。不妨假设该工厂只生产B款口罩，则投入的总生产成本为9000×2=18000元，但题设要求总成本不得高于15000元，则总成本至少要减少18000-15000=3000元，若生产一个A款口罩会节约成本2-1.6=0.4元，故至少需要生产A款口罩的个数为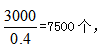选C。

小结：通过例题我们发现，将一定总量的事物分配给不同主体时，可假设将总量全部分配给同一个主体，找到假设方案与题干原始方案的盈亏总量和每份盈亏量，最终求出所需要的份数。

三、巩固加深

训练：现在疫情防控已成常态，四川各地市纷纷建设方舱医院以备不时之需。巴中市现在就正在建设方舱医院工程，已知A工程队单独施工需要30天完成，B工程队单独施工需要25天完成，A工程队单独施工了4天后改为A、B两个工程队一起施工，期间A工程队休息了若干天，最后整个医院建设工程共耗时19天完成，求A工程队中途休息了多少天？（   ）

A.1       B.3      C.5        D.7

【答案】D【解析】分析题意可知此题给定A、B两个工程队单独完工的时间，假设工作总量为150(30和25的最小公倍数)，进而求得A工程队的效率为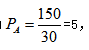B工程队的效率为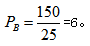要想求解A队中途休息的天数，不妨假设在整个建设工程中A工程队没有休息(A队工作的天数为整个工程的天数)，故整个工程为A工程队先工作4天，再A、B共同合作15天，此时该工程的工作总量为W=4×5+15×(5+6)=185，与实际的工作总量相差35，这多出的工作总量是由于假设A工程队没休息多做的工作，与休息相比A每天多做5，故A工程队多算的工作天数为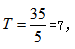说明有7天A工程队是中途休息的，选D。

能够运用盈亏思想解决的题目类型有很多，例如平均数问题，鸡兔同笼问题，工程问题，行程问题，浓度问题等，希望同学们能以点带面，举一反三，灵活运用快速解题。

行测技巧：方阵别慌——找规律，得答案

方阵即正方形阵列，常见的方阵有实心方阵和空心方阵两种。

一、实心方阵

1.模型介绍：

2.规律总结：

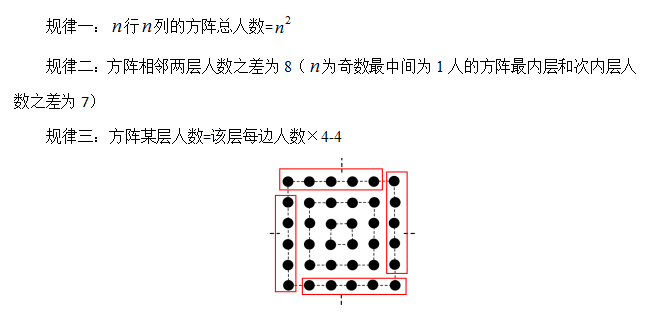
3.例题精讲

例1：某部队的全体官兵刚好排成一个方阵，最外层人数是128人，则该部队共有多少名官兵？（   ）

A.529       B.783      C.1089       D.1122

【答案】C【解析】最外层人数为128人，即最外层每边人数×4-4=128，计算可知最外层每边人数=33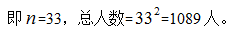，故选择C选项。

例2：某高二年级学生组成方阵，已知该方阵从外向里数第二层人数是100人，那么该方阵总人数为(   )人。

A.529          B.625       C.729          D.784

【答案】D【解析】方阵从外往里数第二层100人，则最外层人数为108人，即最外层每边人数×4-4=108，计算可知最外层每边人数=28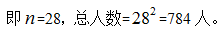，故选择D选项。

二、空心方阵

1.模型介绍

空心方阵是由实心方阵演变而来，即将实心方阵中间掏去若干层。

正中间有一个人的正方形阵列掏去中间若干层，如下图所示为掏去中间一层，任意一层每边人数n为奇数。

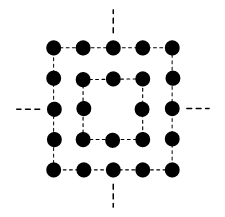
正中间有四个人的正方形阵列掏去中间若干层，如下图所示为掏去中间一层，任意一层每边人数n为偶数。

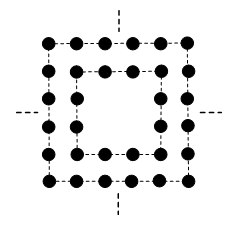
2.规律总结

规律一：方阵相邻两层人数之差为8

规律二：方阵某层人数=该层每边人数×4-4(可理解为正方形的周长=边长×4，拐角处的人均重复计算)

3.例题精讲

例题：小王在装修时，准备在正方形电视墙的外围贴正方形瓷砖，由内到外一层北欧绿色，一层北欧蓝色交替铺，已知共贴了5层，最外层一条边上贴了30块瓷砖，则电视墙的外围共贴了多少块北欧绿色瓷砖？（   ）

A.300      B.324       C.416       D.500

【答案】A【解析】五层瓷砖由内向外的颜色依次为北欧绿色、北欧蓝色、北欧绿色、北欧蓝色、北欧绿色，最外层一边的瓷砖数为30，则最外层共贴30×4-4=116块，由外向内所贴瓷砖数量依次为116块、108块、100块、92块、84块，所用北欧绿色瓷砖共116+100+84=300块。故选择A选项。

大家在备考中需要注意的是，在方阵问题中，若题干中没有明确说明是实心方阵还是空心方阵，则默认为实心方阵。

快速解决整除思想

提到整除思想，首先我们需要明确何谓“整除”，简单来说，如果在一个等量关系M=A×B中，M，A，B三者均为整数，那我们就可以说M能被A或者B整除。那么整除思想又是如何在做题当中进行合理运用的呢，我们一起来看几道题。

例1：教室里有若干学生，走了10名女生后，男生人数是女生的2倍，又走了9名男生后，女生人数是男生的5倍，问最初教室里有多少人？（   ）

A.15        B.20     C.25         D.30

【答案】C【解析】在这道题当中，出现了倍数关系，所以很显然，通过设未知数列方程进行求解肯定是没有问题的，但是相对而言解题时间会略长一些。但是出现谁是谁的几倍这样的表述的时候，一定意味着题目中某些数据之间存在着整除这样的关系，所以按照这种思维进行分析的话，我们不难发现，“走了10名女生后，男生人数是女生的2倍”就意味着最初教室里人数减去10后剩余的人数是女生人数的3倍，也就是说总人数减去10可以被3整除，验证可知只有C选项符合题意，所以直接选C。

例2：学校有足球和篮球的数量比是8：7，先买进若干个足球，这时足球和篮球的数量比是3：2，接着又买进若干个篮球，这时足球和篮球的数量比是7：6。已知买进的足球比篮球多3个，原来有足球(   )个？

A.48       B.42    C.36       D.30

【答案】A【解析】这道题当中出现了明显的比例关系，而无论足球还是篮球都一定是整数个的，所以既然足球和篮球的数量比是8：7，那就意味着足球的个数一定能够被8整除，能被8整除的只有A选项。

例3：若干学生住若干房间，如果每间房间住4人，则有20人没地方住，如果每间房间住8人，则有一间只有4人住，问共有多少学生？（   ）

A.30        B.34     C.40        D.44

【答案】D【解析】因为房间数一定是整数，结合“如果每间房间住4人，则有20人没地方住”可知总人数减去20能被4整除，排除A、B选项。再根据“如果每间房间住8人，则有一间只有4人住，则可知总人减去4能被8整除”，则只有D选项满足。

通过以上几题我们可以对整除进行一个简单的总结，在数量关系题目当中，常见的运用整除思想进行解题的主要有两种类型题，第一种是题干中出现每、平均、倍数、整除等字眼时；第二种是虽然没有出现上述这样的文字表述，但是题干所描述的概念本身具有整数特征，同时题干中有小数、分数、百分数、比例等时，都可以通过整除的思想进行快速解题。

整除思想作为一种非常好用的解题技巧，本身难度也比较小，希望大家能够准确地理解并掌握这种方法，在考试中合理运用，并收获满意的成绩！

溶液混合算浓度，十字交叉解答案

浓度问题是同学们在行测考试中会遇到的一类题型，通常可以利用公式列方程解决问题。简单的浓度问题相信对于大多数同学来说都可以快速得出结果，但遇到溶液的混合问题，就会比较头疼，那么这类问题如何快速解决呢？今天政华公考给同学们讲一讲十字交叉法，这种方法在行测中，无论是数量关系还是资料分析都有所涉及。

一、什么是浓度问题

浓度问题是研究溶质、溶剂、溶液及溶液配比问题。

二、基本计算关系

三、解题思路

难度较低的题目只需要通过以上几个公式列方程即可求解，那么在考试中如果遇到溶液混合这类难以下手的问题，同学们还可以采用十字交叉法来快速求解。

我们先简单了解一下十字交叉的原理：

设A溶液浓度为a，B溶液浓度为b，混合后的浓度为r，则根据混合前后溶质质量相等可列等量关系为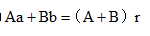

整理可得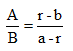

用十字模型表示如下：

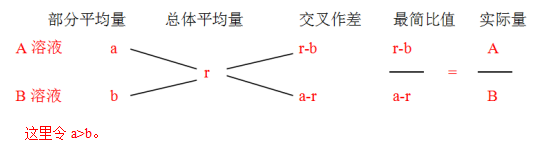
最终结论：沿十字方向交叉作差(大数减小数)，得到列式的比值等于分母比，分母比即在浓度公式中分母部分的溶液质量比。

1.方法对比：

例1：现有浓度为15%和30%的盐水若干，如要配出600克浓度为25%的盐水，则分别需要浓度15%和30%的盐水(   )克。

A.100、500       B.200、400     C.500、100     D.400、200

【答案】B【解析】根据题目已知两份溶液的浓度、溶液质量之和及混合后的溶液浓度，需要求出两份溶液的质量分别是多少。

方法一：由“配出600克浓度为25%的盐水”可知，两份溶液混合，所得的混合后的溶液质量由两份溶液加和而得，即两种溶液质量之和为600克。混合后的溶液浓度为25%，即混合后的溶质质量除以混合后溶液的总质量为25%，混合后的溶质质量为15%溶液的溶质质量与30%溶液的溶质质量加和而得。想要表示15%溶液的溶质质量还需要知道溶液的质量，30%溶液的溶质质量同理。即两个等量关系均与两份溶液质量相关，即可假设浓度15%溶液的质量为x，浓度为30%溶液的质量为y，可列如下方程组：

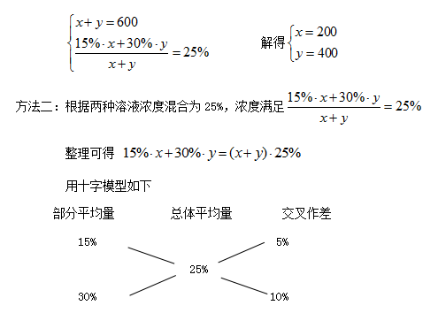
根据交叉作差后的比值为溶液质量之比可得：浓度分别为15%和30%的盐水质量之比为1：2，两份溶液的总质量之和为600克，即将600克的溶液分为3份，15%溶液占1份，30%溶液为2份，故15%的溶液质量为200克，30%浓度的溶液质量为400克。

通过这个例子，我们不难发现，方程法在列式及求解的过程中，计算量相对较大，而通过十字交叉法简单画图就可以快速得出结果，列式步骤较少、计算量较少。因此，同学们可以在今后做题时采用十字交叉法快速解决此类问题。

2.实战运用：

例2：化学实验中，需要使用现有不同浓度的A、B两种氯化钠溶液配置新的浓度为15%的氯化钠溶液。已知A溶液的浓度是B溶液的5倍，且若将50克A溶液与250克B溶液混合即能完成配置，那么A溶液的浓度是(   )。

A.45%         B.40%     C.35%  D.30%

【答案】A【解析 】根据题干“A溶液的浓度是B溶液浓度的5倍”，可假设B溶液浓度为x，则A溶液的浓度可表示为5x。

解得x=9%，所求为A溶液的质量，即5x=45%。

以上两个题目中均涉及两种溶液混合，均可用十字交叉来解决，不仅避免了繁琐的列式，也在一定程度上简化了计算。同时对于十字交叉法之所以可以用在浓度问题是因为存在了比值的混合，在我们考试过程中同学们也可以根据这个特点一一总结学习，例如增长率混合、平均数混合等等都可以举一反三哦！各位同学只需要勤加练习便可掌握此类问题。