行测数量关系常考问题解题技巧

快速解决鸡兔同笼问题

鸡兔同笼问题的历史悠久，大约在1500年前《孙子算经》中就记载了一个有趣的问题。书中是这样表述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉免各几何？”，把这几句话翻译过来就是：有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有94只脚；求笼中各有几只鸡和兔？今天政华公考就根据这道题目，跟大家一起来聊一聊这一类问题。

一、基础的鸡兔同笼问题

1.题型特征

例1：有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有94只脚。求笼中各有几只鸡和兔？

【解析】该题干中涉及了鸡和兔两个主体，并且已知头和脚的总数；根据常识可知一只鸡有1个头、2只脚，一只兔有1个头、4只脚。即已知两个主体(鸡和兔)的指标数(1只鸡有1个头、2只脚和1只兔有1个头、4只脚)和指标总数(共有35个头和94只脚)，也就归纳出了这类题目的题型特征。

题型特征：已知两个主体的两个指标数，两个指标的总数。

2.求解方法

常用的方法是方程法和假设法。

(1)方程法

假设有x只鸡，有y只兔，则根据总共有35个头和94只脚，可得

(2)假设法

如果笼子中的35只都是鸡，那么应该有

只脚，但是实际上有94只脚，因此多出来94-70=24只脚，那为什么会多出来这24只脚呢？

因为只要有一只兔子就会比假设的70只脚多2只脚，则多出来多少个两只就说明有多少只兔子，因此兔子有24÷2=12只，那么鸡的数量就是35-12=23只。

在现在的考试中当然很少会考查这么基础的题目，所以我们来看一下这种题目的变形。

二、鸡兔同笼问题的变形

例2：某工程需要运送一批建材，一辆卡车在晴天每天可运20次，雨天每天只能运12次。该辆卡车连续8天运送了112次，那么运送期间经历的晴天有(   )天。

A.2          B.3        C.4      D.5

【答案】A【解析】根据题干可知：晴天加雨天共8天，晴天和雨天运送了112次。

方法一，设晴天有x天，雨天有y天，则有

方法二，如果8天全是雨天，可运12×8=96次，比实际少运了112-96=16次。每多一个晴天比一个雨天多运20-12=8次，则运送期间经历的晴天有16÷8=2天，故本题选A。

因此我们可以发现，求的是晴天，我们设的是全是雨天，反之如果要我们求的是雨天，就可以设全是晴天，即总结出假设法的思路为设鸡求兔和设兔求鸡。

大家在掌握方程法解鸡兔同笼问题的同时，也可以巧妙地利用假设法提高我们的做题速度，你学会了吗？

交替合作问题之正效率篇

工程问题是我们在学习行测数学运算中比较常见的一种题型，但是这种题型往往容易出现带有陷阱的地方，那就是工程问题中的交替合作问题，在此类问题中可能会出现正效率也有可能出现负效率，所以我们需要在做题的时候分析清楚这两类题目，接下来政华公考带着大家来解决交替合作中的正效率问题。

概念理解

交替合作问题一般指在多个主体下以交替合作的方式去完成某一项工作，并且会以循环的方式进行，直到完成这项工作，所以本质在于周期循环的过程。

例题剖析

例题：一条隧道，甲单独挖要20天完成，乙单独挖要10天完成。如果甲先挖1天，然后乙接替甲挖1天，再由甲接替乙挖1天……两人如此交替工作。那么，挖完这条隧道共用多少天？（   ）

A.11.5     B.12.5    C.13.5       D.14.5

【答案】C【解析】要想求出完成这项工作的时间，我们需要三个数据，分别是工程总量和甲乙的效率和，先用特值法设出隧道的工程总量，即设为20和10的最小公倍数20，那么就可以得出甲和乙的效率分别是1和2，最小的循环周期为2天(甲工作1天，乙工作1天)，一个循环周期的工作量为1+2=3，那么完成20÷3=6…2，则需要6个循环周期还剩下2个工作量，剩余的工作量需要甲做1天，乙做0.5天，再加上之前的6个循环周期(每个循环周期为2天)即12天，一共是13.5天。选择C。

步骤总结

1.设工作总量为时间的最小公倍数；

2.分别求出每个主体的效率；

3.确定好一个循环周期的时间及效率总值；

4.算出该工作总量中的周期个数以及剩余工作量

5.根据题目要求分析剩余工作量所需时间。

实战演练

例题：单独完成某项工程，甲队需要36天，乙队需要30天，丙队需要32天。如果安排合作施工，按照甲乙、乙丙、丙甲、甲乙……的顺序按天轮转，问完成这项工作时，甲工作了多少天？（   ）

A.11天整       B.11天多     C.12天整       D.12天多

【答案】A【解析】第一步：设工作总量为1440(36、30、32的最小公倍数)，第二步：则甲队的效率为1440÷36=40，乙队的效率为1440÷30=48，丙队的效率为1440÷32=45。第三步：甲乙、乙丙、丙甲正好是一个周期，一个周期完成的工作量为(40+48+45)×2=266，第四步：1440÷266=5……110，第五步：甲乙一天完成的工作量为40+48=88，剩余110-88=22的工作量由乙丙完成，需要不到一天的时间。所以一个周期甲做2天和最后剩余量甲做1天，则甲工作的时间为5×2+1=11天。

希望各位同学们能够梳理清楚交替合作问题的题干以及操作步骤，并且在课后之余要多加练习。这样就能够在下次碰到类似的题目时能够快速反应并作答正确。当能够做好正效率交替合作问题时，我们才好进一步去解决负效率的交替合作问题。

行测数量关系：思维铸就基础方法决定效率

众所周知，题量大、时间紧是行测考试的一贯特点，兵贵神速依然是决胜的不二选择。对于数量关系部分，如何快速解题，今天政华公考带领大家通过具体题目感受不同视角的数学思维吧！

例题：某厂为甲、乙、丙三个商店乒乓球的库存地，共存放了6000个乒乓球，工人不小心把甲商店库存中的144个乒乓球错放入乙商店库存后，乙商店的乒乓球个数比丙商店多600个，且此时甲、乙两商店的库存量之比为5∶3，则原来甲商店存有多少个乒乓球？（   ）

A.3130      B.3144     C.3150      D.3160

【答案】B【解析】【视角一】代入验证

根据题干条件，依次代入选项分析验证。代入A项，若原来甲存有3130个乒乓球，则后来甲还有2986个，后来乙丙店合计是3014个，又乙比丙多600个，故后来乙有(3014+600)÷2=1807个。而此时甲、乙库存量之比

2986：1807，不等于5：3，排除；代入B项，若原来甲存有3144个乒乓球，则后来甲还有3000个，后来乙丙店合计是3000个，同理后来乙有(3000+600)÷2=1800个。此时甲、乙之比3000：1800等于5：3，且此时题干条件已全部满足，作为只有唯一答案的单选试题，选择B项即可。

【视角二】方程思想(设多个未知数)

设原来甲、乙、丙分别存有x、y、z个乒乓球，由三店库存总量为6000个可得x+y+z=6000①；后来将甲店的144个球错放入乙店后，甲、乙的数量分别为x-144、y+144个，丙店数量依然为z个，由条件得y+144-z=600②，且有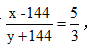得3x-5y=1152③，①+②得x+2y=6456④，③×2+④×5得11x=34584，x=3144。选择B项。

【视角三】方程思想(设一个未知数)

根据题意，当把甲店中的144个乒乓球错放入乙店后，甲、乙两店的库存量之比为5：3，可设后来甲、乙的库存分别为5x、3x个，则丙商店后来应有6000-5x-3x个，又因乙店的个数比丙店多600个，得3x-600=6000-5x-3x，解得x=600，则甲商店原来的库存为600×5+144=3144个。选择B项。

【视角四】整除思想

由题意知，甲店原有库存个数减去144后，是5的倍数，结合选项，只有B项满足。选择B项。

综上所述，多方式分析同一道题目，切入点不同，对应难度亦不同，使用环境也不同。代入验证是最粗略的方法，优点是思考量少，缺点是有可能需要较长时间；方程思想是最基础的方法，优点是适用性广，对于含有明显等量关系的题目皆可使用，并且通过对比视角二和视角三，发现设多个未知数列方程时思考量较少，设较少未知数列方程时计算量则较少；视角四整除思想技巧性较强，很多复杂情况都能快速解决，但其具体解题速度可能会受制于选项数值的设置。

正所谓“思维铸就基础，方法决定效率”，至于考场上具体用什么方法，大家只有在平常多储备、多学习，才能到时练就一双慧眼、以速制胜。

行测函数图像问题的应对小妙招

函数问题是结合图像的方式来展示数学关系的问题，这类问题看上去比较难，但实际上在行测考试中，解决函数问题还是有章可循有据可依的。行测考试中涉及到的函数主要包括三种函数，分别为常函数、一次函数、分段函数，一般不会涉及到过于复杂的函数类型。一般来说解决此类问题需要注意以下四个方面，具体如下：

(1)确定函数与x轴、y轴的交点。即y=0时x的取值(与x轴交点)、x=0时y的取值(与y轴的交点)；

(2)判断函数是否具有周期性、分段等特性，并找到分段函数的分段点。

(3)判断函数是否为直线。常函数或等比例变化的函数(一次函数)图像均为直线，其他复杂的函数可能出现曲线。

(4)描出不同分段内的部分点，重点描出最大值或最小值点。

总之，只要把握函数图像的范围、最高点最低点以及极点、变化趋势即单调性周期性对称性等核心，那么常见的图像类问题就能有效解决。接下来我们来看两道题目：

例1：甲和乙两条自动化生产线同时生产相同的产品，甲生产线单位时间的产量是乙生产线的5倍，甲生产线每工作1小时就需要花3小时时间停机冷却而乙生产线可以不间断生产。问以下哪个坐标图能准确表示甲、乙生产线产量之差(纵轴L)与总生产时间(横轴T)之间的关系？（   ）

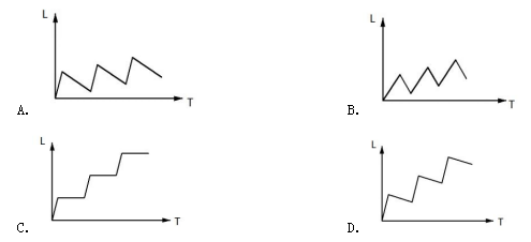
【答案】A【解析】甲以4小时为一周期工作，乙连续工作，所以两者产量差应具有周期性。甲每工作工作1小时就需要冷却3小时，所以在每个工作周期内部应该是以1：3的时间分段的，排除B项。再考虑每个周期结束后的甲、乙产量差，设甲的工作效率为5、乙为1，每个周期(4小时)的产量差为5-4×1=1，斜率为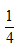，即原点到每个周期结束点的连线所形成的直线斜率为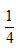，而选项C、D的斜率都为1，排除C、D。故选A。

例2：某饲料厂原有旧粮库存Y袋，现购进X袋新粮后，将粮食总库存的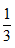精加工为饲料。被精加工为饲料的新粮最多为A1袋，最少为A2袋。如所有旧粮、新粮每袋重量相同，则以下哪个坐标图最能准确描述A1、A2分别与X的关系？（   ）

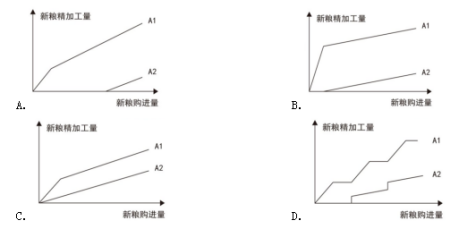
【答案】A【解析】A2曲线：若想要新粮加工量最少，需要先加工旧粮，说明A2必须有一段纵轴值为0的横线，排除C项；A1曲线：若想要新粮加工量最多，则需要先加工新粮，旧粮Y是不变量，不存在周期性，排除D；观察A、B选项，区别在于A1曲线第一段的斜率，代表的是尽量多的使用新粮的起始阶段，此时应该全部使用新粮，斜率为1，A项符合。故选A。

通过以上例题各位考生会发现，函数图像问题简单应用其实并不难，在公务员考试的备考过程中掌握解题思路就能够顺利解决函数图像问题。在备考过程中，可能会遇到较为复杂的函数图像题目，在读题时认真审题，灵活应用解题思路，切勿生搬硬套。

行程问题之平均速度

在行测数量关系中，行程问题几乎每年必考，不少考生认为该问题较难，选择放弃。其实把行程问题细分为各小题型，会发现其中有很多小题型因为有特定的求解思路和方法，还是比较简单易学的。今天，政华公考就带大家一起学习其中一类只需根据基本公式就能解题的小题型——与平均速度有关的行程问题。

基础知识

例题精讲

例1：一辆汽车第一天行驶了5个小时，第二天行驶了600千米，第三天比第一天少行驶200千米，三天共行驶18小时，已知第一天的平均速度与三天全程的平均速度相同，则三天共行驶了多少千米？（   ）

A.800        B.900      C.1000        D.1100

【答案】B【解析】设第一天和三天全程的平均速度均为v千米/时，则第一天行驶距离为5v千米，第三天行驶距离为(5v-200)千米，根据“第一天的平均速度与三天全程的平均速度相同”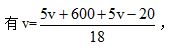，解得v=50，则三天共行驶了18×50=900千米，故本题选B。

例2：小伟从家到学校去上学，先上坡后下坡。到学校后，小伟发现没带物理课本，他立即回家拿书(假设在学校耽误时间忽略不计)，往返共用时36分钟。假设小伟上坡速度为80米/分钟，下坡速度为100米/分钟，小伟家到学校有多远？（   ）

A.2400米       B.1720米     C.1600米    D.1200米

【答案】C【解析】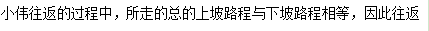

小结：1.此类题目的特征是题干出现“平均速度”的字眼。2.阅读题目后，需要判断本道题目的平均速度应该使用哪一个公式。

通过以上题目的学习，政华公考相信大家对于平均速度相关的题目，以及各个公式的应用有了一定的了解。希望各位同学在平时做题过程中能够多加练习，真正做到融会贯通，熟能生巧。