行测数量关系常见题型如何解答
行测数量关系常见题型之流水行船问题
在行测考试中，数量关系部分会考查很多题型，流水行船问题就是其中之一。流水行船问题是指船在江河里航行时，除了本身的前进速度外，还受到流水的推送或顶逆作用，在这种情况下计算船只的航行速度、时间和所行路程的问题。
流水行船属于行程问题的一种，解题的基本公式为：路程=速度×时间，不过与其他行程问题不同的是，速度受到水速的影响，具体计算路程时，利用的是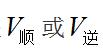
。具体如下：
接下来请大家利用上述公式求解下列题目。
【例题1】A、B两港相距240千米，一艘轮船从A港出发顺流而下，用了6小时到达B港。若静水中轮船的速度为36千米/小时，则这艘轮船从B逆流而上到A港需要多长时间？（ ）
A.6.5 B.7 C.7.5 D.8
【答案】C【解析】题干表述的是船在水中行驶，属于流水行船。题目已知A、B的距离，顺流而下用的时间，则根据行程基本公式，可得轮船顺水速度：
【例题2】甲、乙两港相距720千米，一轮船往返两港之间，顺流航行需要15小时，逆流航行需要20小时。问水流速度是多少千米/小时？（ ）
A.4 B.5 C.6 D.7
【答案】C【解析】船在水中行驶，属于流水行船问题。已知路程和时间，可以求出速度。轮船顺流航行速度：
通过上述题目的讲解，相信大家能对流水行船问题有了更深入的了解，解题的关键是梳理好船只的运行过程，明确顺流还是逆流，进而结合流水行船的相关公式进行计算。
行测利润问题的“左膀右臂”：列表和特值
在行测数量关系中，利润问题总是无法回避的一类题型。不论遇到简单利润问题，还是复杂利润问题，其实我们都可以通过题干中存在的等量关系，设未知数、列方程进行求解。但是当碰到一些复杂利润问题的时候，可能大家都知道用方程的思想，但却无从下手，所以，今天政华公考就带大家一起来了解复杂利润问题求解过程中两个重要的方法：列表和特值。
一、方法介绍
列表的常见应用：求解复杂的利润问题，可通过列表的方式整理题干数据、梳理题干信息，如题目涉及商品分批销售、多个商家或多种类型商品进行销售时。
特值的常见应用：复杂利润问题的题干中通常有关于“量”的表述，且通过百分数、比值形式给出，此时可设“量”为特值简化运算，如利润问题中经常涉及的销量、产量等。
二、小试牛刀
例1：某家具店购进一批桌椅，每套进价200元，按期望获利50%定价出售。卖掉这批桌椅的60%以后，店主为提前收回资金，打折出售余下的桌椅。售完全部桌椅后，实际利润比期望利润低了18%。问余下的桌椅是打几折出售的？（ ）
A.七五折 B.八二折 C.八五折 D.九五折
【答案】C【解析】家具店的桌椅分两批销售——原价出售和打折出售，结合销量以百分数的形式呈现，可特值桌椅的数量总量为10，梳理题意列表如下：
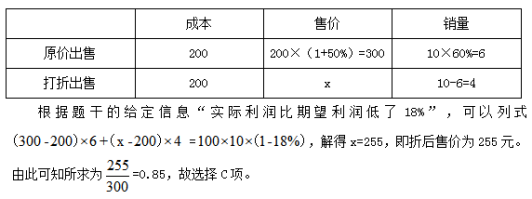
例2：为降低碳排放，企业对生产设备进行改造，改造后日产量下降了10%，但生产每件产品的能耗成本下降了50%，其他成本和出厂价不变的情况下每天的利润提高了10%。已知单件利润=出厂价—能耗成本—其他成本，且改造前产品的出厂价是单件利润的3倍，则改造前能耗成本为其他成本的：（ ）
【答案】B【解析】企业改造前、改造后产品的部分量发生变化，结合日产量以百分数的形式呈现，可特值改造前日产量为10，梳理题意列表如下：
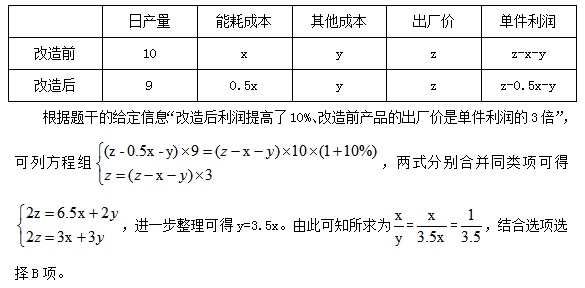
通过上述两道题目不难发现，当遇到复杂利润问题的时候，列表可以帮助我们更好地梳理题干信息和表示一些过程量；特值可以减少我们设未知数的数量，从而简化计算过程。所以列表和特值仿佛就是复杂利润问题求解过程中的左膀和右臂，两者相互结合，降低了我们理解题干信息和求解题目答案的难度。
行测数量关系中不定方程如何解
在行测数量关系考试中，会有一些经常考查的知识点，比如方程，这种题目还是比较容易做对，但是需要大家注意，对于特殊的方程即不定方程(未知数的个数多于方程的个数)的求解需要引起重视。那这类方程该如何求解呢？接下来，政华公考给大家分享不定方程的三种在正整数范围内的解题方法。
一、整除法
应用范围：未知数的系数与常数项有非1公约数。
应用方法：根据所列方程中各因式所具备的整除特性，判断出所求结果具备的整除特性，从而排除选项。
例题1：某国家对居民收入实行下列税率方案：每人每月不超过3000美元的部分按照1%税率征收，超过3000美元不超过6000美元的部分按照X%税率征收，超过6000美元的部分按Y%税率征收(X，Y为整数)。假设该国某居民月收入为6500美元，支付了120美元所得税，则Y为多少？（ ）
A.6 B.3 C.5 D.4
【答案】A【解析】由题意“收入为6500美元，支付了120美元”，6500超过6000，所以总的所得税可由三个阶段所得税加和得到，即3000×1%+3000×X%+500×Y%=120，化简可得6X+Y=18，Y=6×(3-X)，由于X、Y均为整数，则3-X为整数，Y等于6乘以整数，因此Y是6的倍数，只有A项是6的倍数，选择A项。
二、奇偶性
应用范围：未知数的系数一奇一偶。
应用方法：根据所列方程中各因式所具备的奇偶特性，判断出所求结果具备的奇偶特性，从而排除选项。
例题2：某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师，培训中心将所有的钢琴学员和拉丁舞学员共76人分别平均地分给各个老师带领，刚好能够分完，且每位老师所带的学生数量都是质数。后来由于学生人数减少，培训中心只保留了4名钢琴教师和3名拉丁舞教师，但每名教师所带的学生数量不变，那么目前培训中心还剩下学员多少人？（ ）
A.36 B.37 C.39 D.41
【答案】D【解析】设每位钢琴教师带x名学生，每位拉丁舞教师带y名学生，且x、y为质数，教师总共带76名学生，所以5x+6y=76。根据乘法和加法奇偶性的判断，偶数乘以奇数和偶数的结果都为偶数，偶数加奇数结果为奇数，偶数加偶数结果为偶数，所以6y是偶数，由于76是偶数，则5x为偶数，5不是偶数，则x必为偶数。然而x又为质数，根据“2是唯一的偶质数”可知，x=2，代入原式得，y=11。现有4名钢琴教师和3名拉丁舞教师，每名老师所带学生人数不变，则剩下学员4×2+3×11=41人。因此选择D。
三、尾数法
应用范围：未知数系数是5或5的倍数。
应用方法：根据所列方程中各因式的尾数，判断出所求结果的尾数特点，从而排除选项。
例题3：有271位游客欲乘大、小两种客车旅游，已知大客车有37个座位，小客车有20个座位。为保证每位游客均有座位，且车上没有空座位，则需要大客车的辆数是( )。
A.1辆 B.3辆 C.2辆 D.4辆
【答案】B【解析】设大客车需要x辆，小客车需要y辆，共乘坐271人，则37x+20y=271。y的系数是20，为5的倍数，可考虑尾数法，20y的尾数是0，271的尾数为1，则37x的尾数是1，结合选项可知，x=3满足题意，选择B项。
行测数量关系：“整除”帮你提提速
数量关系是行测考试的一个部分，同时也是难点。很多考生数量关系部分的得分很低，一个重要的原因就是做题速度慢，在考试中能够完成的题目太少。那该如何打破壁垒呢？当然是学习一些快速解题的技巧，今天政华公考就带领大家学习其中一种技巧——整除。
应用整除之前，先带大家了解下整除的相关内容。
一、整除的概念
若a÷b=c(a、b、c均为整数)，则a能被b整除。示例：6÷3=2，即6能被3整除。
二、整除的核心
通过题干中所给的信息，判断结果应具备的整除特性，从而排除错误选项。
示例：某高中甲班共有不到50个人，男生占总数的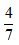
，那么甲班可能有多少人？（ ）
A.36 B.41 C.42 D.47
【答案】C【解析】根据“男生占总数的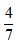
”可知，甲班的学生总数应可被7整除，代入4个选项，其中A、B、D均不可被7整除，排除，C项42可以被7整除，符合条件，选择C项。
三、应用整除的题型特征
1.题干文字描述中出现“整除、平均、每、倍”等字眼。
示例：某班级组织学生春游，如果每辆车坐6人，最后剩余5人没有车坐。
(班级总人数-5)=车辆数×6，则班级总人数减去5后应可被6整除。
2.题干出现“分数、百分数、比例”等特征数据。
示例：甲、乙两个班级的人数之比为12∶17。
甲班人数可以平均分成12份，乙班人数可以平均分成17份。故甲班人数可被12整除，乙班人数可被17整除。
结合以上内容，我们一起看看下边的题目如何应用整除快速求解。
例1：教室里有若干学生，走了10名女生后，男生人数是女生的2倍，又走了9名男生后，女生人数是男生的5倍，问最初教室里有多少人？（ ）
A.15 B.20 C.25 D.30
【答案】C【解析】题目中出现了“倍”这个字眼，可以考虑应用整除解题。由“男生人数是女生的2倍”可知，此时男、女生的总人数是3的倍数，即被3整除；根据“女生人数是男生的5倍”，可知此时男、女生的总人数是6的倍数，即被6整除。题目所求为最初教室里的人数，此数能与“男生人数是女生的2倍”建立联系，即最初教室里的人数减10后，能被3整除，得到这一整除信息后，结合选项开始应用整除，A项15-10=5不能被3整除，排除；B项20-10=10不能被3整除，排除；C项25-10=15，15可以被3整除，符合题意；D项30-10=20不能被3整除，排除。综上，只有C选项符合题意，直接选C。
例2：某单位有工作人员48人，其中女性占总人数的37.5%，后来又调来女性若干人，这时女性人数恰好是总人数的40%，问调来几名女性？（ ）
A.1 B.2 C.3 D.4
【答案】B【解析】题目中出现了“37.5%，40%”两个百分数，可以考虑应用整除来解题。结合例1，寻找所求量的整除关系，与调来的女性人数相关的数据是40%，40%=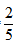
，由此可推出调了若干名女性后，总人数可被5整除，总人数=原有工作人员数量+调来的女性人数=48+新调来的女性人数，结合选项开始应用整除，A项48+1=49不能被5整除，排除；B项48+2=50能被5整除，符合题意；C项48+3=51不能被5整除，排除；D项48+4=52不能被5整除，排除；只有B选项符合题意，选择B项。
小结：应用整除时，需要先寻找与所求量相关的整除关系，整除关系往往需要通过题型特征里表述的文字或数据进行确定，确定整除关系后再结合选项代入排除即可。
通过以上的学习，希望大家能够对整除有所了解，备考做题时遇到了满足应用整除的题型特征题目时，大胆尝试利用整除去求解，通过练习尽快熟悉这种方法，争取在考场上能够使用这种方法快速解题。
行测数量关系：不要做“井底之蛙”，要学会“跳井”
行测数量关系部分的题目虽然整体较难，但很多题目有固定解法，只要按部就班，轻松做对不是梦，“青蛙跳井”问题就是此类问题的代表。今天政华公考就带大家向上“跳一跳”，通过两道例题来学习一下“青蛙跳井”问题的解题思路。
例1：一口井深24米，有一只青蛙坐落于井底，它白天能向上跳6米，晚上又会下落4米，请问这只青蛙在第几天能跳出井口？（ ）
A.9 B.10 C.11 D.12
【答案】B【解析】大部分人的思路可能是这样的：因为青蛙每天白天向上跳6米，晚上又下滑4米，所以整体来看每天(即一个周期)能向上跳2米，井深24米，由此得出青蛙需要24÷2=12天才能跳出此井。这种解法其实是错误的。我们可以通过一个例子来说明：假如这个井深6米，那青蛙其实在第1天白天就刚好可以跳出井口，但是按照前面那个思路算的话是需要3天才能跳出去的，错的地方就在于“在高度足够低的情况下，不用完成整个周期就可以直接跳出去”，所以我们计算的时候这一部分要单独讨论。回到题目，这道题的关键就在于青蛙最后一天的白天就可以直接跳出井口，不需要再往下滑了，所以我们需要先预留出最后一天白天可以跳出井的距离6米，剩余的24-6=18米再按照整个周期去算天数，所以青蛙是完整地度过前18÷2=9天之后，第10天的白天跳出井口的。选择B项。
“青蛙跳井”题型总结
1.题型特征：做某件事情，工作过程具有周期性且周期内效率有正有负。
2.解题步骤：
①明确任务总值、循环周期、每个周期完成量和周期内完成峰值。
②总值-周期内完成峰值，之后再计算周期数。
③分析若干周期后剩余量的完成时间，计算总时间。
例2：某小区快递站第一天送出快递250件，第二天送出快递420件，第三天接收快递550件。依此规律，第四天送出快递250件，第五天送出快递420件，第六天接收快递550件，该快递站目前有快递1870件，问该快递站到第几天时刚好可以把快递全部送出？（ ）
A.32 B.33 C.34 D.36
【答案】A【解析】快递的送出情况为+250、+420、-550、+250、+420、-550…，由此可见3天为一个周期，每个周期可送出250+420-550=120件快递。我们知道刚好送完快递的时间肯定是在送出快递的那天，所以计算方式依然是先预留出最后两天可以送出的最多的量250+420=670件快递，剩余的1870-670=1200件快递全部送出需要1200÷120=10个周期，也就是30天，因此刚好送完的时间为第30+2=32天。选择A项。
政华公考相信大家通过这两道题已经对“青蛙跳井”问题的问法及基本解法有了一定的了解，大家下去之后一定要多练习多总结，加油！
