行测数量关系：快速解方程

行测数量关系：用对方法来拿下不定方程

在行测考试中，会常常考到不定方程，不定方程的定义是：未知数的个数多于独立方程的个数，对于不定方程来说解题过程和普通方程是类似的，都是根据题干信息寻找等量关系然后再设未知数列式进行求解就可以，但是不定方程的难点就是如何去解方程，很多同学列完等式后总是感觉下一步不知道如何求解，今天就给大家讲解不定方程的四种解题方法。

方法一：带入排除法：将选项带入题干中看是否符合题干要求即可。

【例1】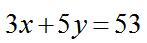，已知x、y为正整数，则x、y分别为：（   ）

A.3、4       B.4、5     C.5、6         D.6、7

【答案】D【解析】将选项依次代入，A项，当x=3时y不是正整数，排除，带入B、C同理，只有带入D项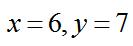，时，满足等式，故答案为D。

方法二：整除法：当未知数的系数与常数项存在不是1的公约数时，可以选择此方法进行求解。

【例2】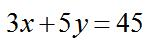，已知x、y为正整数，则x=(   )

A.5          B.7       C.9         D.11

【答案】A【解析】观察等式左右两边，5y和45有一个公约数5，说明5y和45都能被5整除，由此可知3x也能被5整除，即x能被5整除，结合选项，选择A。

方法三：尾数法：未知数的系数带5或者0时，可用尾数法进行求解。

【例3】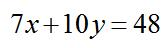，已知x、y为正整数，则x=(   )

A.2         B.4           C.5         D.7

【答案】B【解析】观察等式可知，10乘以任何数其乘积尾数都会是0，所以10y的尾数一定为0，48的尾数为8，则可知7x的尾数一定为8，结合选项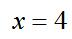，选择B。

方法四：奇偶性：当两个未知数的系数为一奇一偶时，利用数值的奇偶性进行计算。

【例4】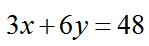，若x、y为正整数且x为质数，则x=(   )

A.2         B.3         C.6         D.7

【答案】A【解析】观察等式左边，未知数系数一个为奇数，一个为偶数，则尝试利用奇偶性进行求解，6y和48均为偶数，根据“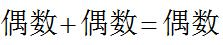”可得3x为偶数，即x为偶数，排除B、D，又根据题干要求x为质数，质数就是除了1和本身之外没有其他公约数的数，排除C，则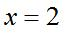，故选择A。

希望通过学习了以上的方法，对大家做不定方程的题有所帮助，在备考时多练习，熟能生巧之后不再为解不定方程而苦恼。

行测数量关系解题的“万能”方程法，你真的会用么？

数量关系一直是行测考试中最让大家头疼的部分，由于不熟悉解题思路，很多同学遇到这类题目往往就有了放弃的心态。但是，数量关系中有一部分的题目，难度系数不大且易于得分，并且采用我们最熟悉的方程法就可以解题。那么，这部分题目其实就是我们突破数量关系这一类难题的关键。

利用方程解题的核心是构造等量关系。虽然很多同学已经接触过方程法很长时间，但是并不知道如何找等量关系去列方程，今天就详细地给大家讲解一下。

构造等量关系时一般分为有明显标志词以及没有明显标志词两种考查方式。

一、题中等量关系明显时，可根据明显的等量关系标志词或基本数量关系构造等量关系。如：根据“是、等、共、占、相当于、比…多/少、倍”等明显的等量关系标志词构造等量关系。“是、等、共、占、相当于、比”就是“=”，“多”就是“+”，“少”就是“-”，“倍”就是“×”。

【例1】甲、乙、丙、丁4人捐款，甲捐款是丙的2倍，甲比乙少捐款40元，其中甲、乙、丙共捐款240元，甲、丙、丁共捐款190元。请问丁捐款多少元？（   ）

A.70         B.80       C.90        D.120

【答案】A【解析】由题干信息可知甲捐款是丙的2倍，若假设丙捐款x元，则甲捐款为2x元；已知甲比乙少捐款40元，则乙捐款2x+40元；由于其中甲、乙、丙共捐款240元，根据“共”可构建等量关系，2x+2x+40+x=240，解得x=40元，即丙捐款为40元，则甲捐款80元，乙捐款120元。由最后条件可知，甲、丙、丁共捐款190元，可求解丁捐款为190-80-40=70元，故本题选A。

二、题中等量关系不明显时，可结合基本数量关系构造等量关系。如题目中给出不同方案对比，就可以根据题目中的不变量构造等量关系。这类题目侧重对题意理解后建立等量关系求解。

【例2】某企业员工组织周末自驾游。集合后发现，如果每辆小车坐5人，则空出4个座位；如果每辆小车少坐1人，则有8人没坐上车。那么，参加自驾游的小车有：（   ）

A.9辆      B.10辆      C.11辆       D.12辆

【答案】D【解析】通过分析题目我们发现，题干中给出了不同的乘车方案，但不论每辆车怎么去分配人员，总人数不会发生变化，那么我们可以结合总人数不变构建等量关系。若假设有x辆车，由题目信息可得，5x-4=(5-1)x+8，解得x=12辆，故本题选D。

以上就是行测考试中构建等量关系的两种常用方法，大家在学习之后要多加练习，熟练掌握，早日攻破数量难关。

行测数量关系：让“比例”帮你快速解方程

在行测学习过程中，大家经常对数量关系望而止步，除了题目略有难度以外，更多的是时间不够的问题。相信有一部分同学在做题过程中，已经列出来了方程，但由于所列方程过于复杂，导致解方程的难度增加或是用了很长时间才解出一道题。为了让大家能够更快速地解出方程，节省做题时间，今天给大家带来一个简单的做题技巧，利用“比例”帮我们列出相对简单的等量关系，从而达到快速解方程的目的。

设未知数一般有直接设和间接设两种方式。直接设是求什么就设什么为未知数；间接设是为简化求解过程，设与所求量相关的量为未知数。题目直接设或间接设核心关键取决于题干的描述方式。

一、题目条件存在多个未知量，设与题目条件最多的相关量为未知数。

【例1】已知2017年、2018年和2019年全球共发射卫星1132颗，2019年发射的卫星数量是2017年的1.5倍还多2颗，2018年比2017年多31颗，则2019年全球共发射卫星：（  ）

A.314颗      B.345颗       C.452颗       D.473颗

【答案】D【解析】由题干信息可知2019年发射的卫星数量是2017年的1.5倍还多2颗，2018年比2017年多31颗，既然2019年和2018年的卫星数量均与2017年有关，那么可以假设2017年卫星数量为x颗，则2019年卫星数量为1.5x+2颗，2018年卫星数量为x+31颗；由2017年、2018年和2019年全球共发射卫星1132颗，可构建等量关系，x+x+31+1.5x+2=1132，解得x=314颗，则所求2019年全球共发射卫星为1.5×314+2=473颗，故本题选D。

二、题目条件存在未知量间的比例关系，设比例的一份为未知数。需要注意的是，我们所说的未知量间的比例关系，并不单单指的是比例，也包括分数、百分数、倍数等。

【例2】甲、乙两个学校的在校生人数之比为5∶3，甲学校如果转入30名学生，再将85名学生转到乙学校，则两个学校在校生人数相同。那么，甲学校原来的在校生人数为多少人？（   ）

A.200         B.250       C.300     D.350

【答案】D【解析】通过题目可知，甲、乙两个学校的在校生人数之比为5∶3，存在未知量间的比例关系，为了方便计算，可以设比例的一份为未知数x，即甲的在校生人数为5x人，乙的在校生人数为3x人。甲学校如果转入30名学生，再将85名学生转到乙学校，则两个学校在校生人数相同，可以构建等量关系，5x+30-85=3x+85，解得x=70人，则所求为70×5=350人，故本题选D。

以上就是行测考试中利用比例巧妙设未知数，从而可以快速解出方程。希望大家可以在学习之后要多加练习，熟练掌握，早日攻破数量难关。

行测数量关系中不定方程如何解

在行测数量关系考试中，会有一些经常考查的知识点，比如方程，这种题目还是比较容易做对，但是需要大家注意，对于特殊的方程即不定方程(未知数的个数多于方程的个数)的求解需要引起重视。那这类方程该如何求解呢？接下来，给大家分享不定方程的三种在正整数范围内的解题方法。

一、整除法

应用范围：未知数的系数与常数项有非1公约数

应用方法：根据所列方程中各因式所具备的整除特性，判断出所求结果具备的整除特性，从而排除选项。

例题1：某国家对居民收入实行下列税率方案：每人每月不超过3000美元的部分按照1%税率征收，超过3000美元不超过6000美元的部分按照X%税率征收，超过6000美元的部分按Y%税率征收(X，Y为整数)。假设该国某居民月收入为6500美元，支付了120美元所得税，则Y为多少？（   ）

A.6       B.3      C.5       D.4

【答案】A【解析】由题意“收入为6500美元，支付了120美元”，6500超过6000，所以总的所得税可由三个阶段所得税加和得到，即3000×1%+3000×X%+500×Y%=120，化简可得6X+Y=18，Y=6×(3-X)，由于X、Y均为整数，则3-X为整数，Y等于6乘以整数，因此Y是6的倍数，只有A项是6的倍数，选择A项。

二、奇偶性

应用范围：未知数的系数一奇一偶

应用方法：根据所列方程中各因式所具备的奇偶特性，判断出所求结果具备的奇偶特性，从而排除选项。

例题2：某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师，培训中心将所有的钢琴学员和拉丁舞学员共76人分别平均地分给各个老师带领，刚好能够分完，且每位老师所带的学生数量都是质数。后来由于学生人数减少，培训中心只保留了4名钢琴教师和3名拉丁舞教师，但每名教师所带的学生数量不变，那么目前培训中心还剩下学员多少人？（   ）

A.36       B.37     C.39      D.41

【答案】D【解析】设每位钢琴教师带x名学生，每位拉丁舞教师带y名学生，且x、y为质数，教师总共带76名学生，所以5x+6y=76。根据乘法和加法奇偶性的判断，偶数乘以奇数和偶数的结果都为偶数，偶数加奇数结果为奇数，偶数加偶数结果为偶数，所以6y是偶数，由于76是偶数，则5x为偶数，5不是偶数，则x必为偶数。然而x又为质数，根据“2是唯一的偶质数”可知，x=2，代入原式得，y=11。现有4名钢琴教师和3名拉丁舞教师，每名老师所带学生人数不变，则剩下学员4×2+3×11=41人。因此选择D。

三、尾数法

应用范围：未知数系数是5或5的倍数

应用方法：根据所列方程中各因式的尾数，判断出所求结果的尾数特点，从而排除选项。

例题3：有271位游客欲乘大、小两种客车旅游，已知大客车有37个座位，小客车有20个座位。为保证每位游客均有座位，且车上没有空座位，则需要大客车的辆数是(   )。

A.1辆        B.3辆     C.2辆      D.4辆

【答案】B【解析】设大客车需要x辆，小客车需要y辆，共乘坐271人，则37x+20y=271。y的系数是20，为5的倍数，可考虑尾数法，20y的尾数是0，271的尾数为1，则37x的尾数是1，结合选项可知，x=3满足题意，选择B项。

以上就是为大家介绍的不定方程的解题方法，希望考生能够熟练掌握学以致用，从而达到快速解题的目的。