政华教育

【答案】D【解析】题干已知不同范围的利润额按照不同的百分比提成，因此每部分的提成需要分别计算，利润10万元以内的部分提成为10×5%=0.5万元；10万元至20万元之间的部分提成为10×7.5%=0.75万元；高于20万元的部分提成为20×10%=2万元。总提成为0.5+0.75+2=3.25万元。故本题选D。

以上三类计算问题均考查考生的基本数学能力，备考重点是重新归纳总结基础知识，夯实基础。

避开行测数量关系中的易错点

数量关系是行测必考题型之一。其题目灵活多变，应试者在作答此类题目时如果不够细心，就会容易出错。接下来，就针对行测数量关系里面比较容易出错的题目，以题带点，简单总结，让大家在备考时能灵活应对。

一、单位换算易错

例：某助农项目从农民手中以1元/斤的价格收购一批芒果，通过网络平台销售，定价30元/10斤包邮，售出芒果的60%后调价为35元/10斤，售完全部芒果的总收入比调价前预计的多20万元。问：这批芒果总重量为多少吨？（）

A.50 B.100 C.500 D.1000

【答案】C【解析】已知芒果的进价为1元/斤，调价前的售价为30元/10斤，即3元/斤，调价后的售价为35元/10斤，即3.5元/斤。设这批芒果的总重量为x斤，则调价前预计的总收入为3x元，实际总收入为3×60%x+3.5×(1-60%)x=3.2x元，则根据“售完全部芒果的总收入比调价前预计的多20万元”可得，3.2x-3x=200000，解得x=1000000，1吨=1000千克=2000斤，故这批芒果的总重量为1000000÷2000=500吨。

易错分析：此题易错选项为D，原因是将1000斤看成1吨，而1吨其实是1000千克，1千克等于2斤，因此1吨=2000斤。

避错指导：当题目中同一计量单位不统一时，一定要注意单位换算。公考中常见的换算单位如下：1小时=60分=3600秒；1米/秒=3.6千米/时；1公顷=100公亩=15亩=10000平方米；1吨=1000千克、1市斤=0.5公斤=0.5千克。

二、数据处理易错

例：两辆汽车同时从两地相向开出，甲车每小时行驶60千米，乙车每小时行驶48千米，两车在离两地中点48千米处相遇，则两地相距( )千米。

A.192 B.224 C.432 D.864

【答案】D【解析】设甲、乙经过t小时相遇，结合题意作图如下，根据图中线段关系可得，60t-48=48t+48，解得t=8，故两地相距(48t+48)×2=864千米。

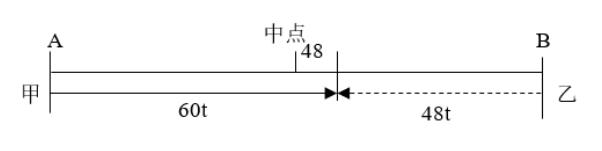
易错分析：此题易错选项为C，原因是以为甲比乙多行驶的路程为48千米，以此为路程差得到60t-48t=48，解得t=4，进而得到两地距离为(60+48)×4=432千米。实际上，甲行驶的路程比全程的一半多48千米，乙行驶的路程比全程的一半少48千米，因此甲比乙多行驶的路程为48+48=96千米。

避错指导：遇到此类问题，建议解题时将中间量或者说是“桥梁”量表示出来，再进行求解，如本题中可将两地距离设为S，则一半的距离为0.5S，甲行驶的路程为0.5S+48，乙行驶的路程为0.5S-48，进而可得60t-48t=0.5S+48-(0.5S-48)=96，如此便可避免错误。

三、和定最值易错

例：小李期末考试6门功课的平均分是90分，分数最高的功课考了95分，那么他这次期末考试分数最低的功课最低考了多少分？（）

A.80 B.75 C.65 D.60

【答案】C【解析】要使分数最低的功课考的分数最低，则应使其它功课的分数尽可能高，最高可均为95分，则所求为90×6-95×5=65分。

易错分析：此题易错选项为B，和定最值题目的题干描述一般为“各量均为整数且互不相等”，易错项就是将6门功课的得分看成了互不相等，其实此题没有要求每门课程得分互不相等，也就是部分功课得分可以相等。

避错指导：遇到已知几个数的和，求其中某个数的最大/小值的题目，即和定最值题目时，重点注意题干表述，是否要求各量互不相等，若无要求，则各量可按相等计算。

以上就是行测数量关系解题中常见的几个易错点，文中给出了相应的避错指导，希望大家做题时能够避免，取得好的行测成绩。

行测数量关系：神奇三角形在哪里

几何问题是行测数量关系中的常考题型之一，而很多同学在复习的时候，会觉得几何问题中所涉及的图形知识太多了，比如单纯平面几何图形就包含正方形、长方形、梯形、菱形、平行四边形、圆形等，考试中有可能考查这些图形的周长和面积，甚至会考查一些图形特有的性质。这就导致复习的时候，要兼顾的重点太多，大量的公式及性质造成巨大的记忆负担，使得很多同学会知难而退，干脆不去复习几何问题，更有甚者连整个数量都放弃掉了。今天给同学们指一条解答几何问题的明路就是三角形，它的考察频率高，考点技巧通俗易懂，尤其是那神奇的三角形——直角三角形，下面一起来学习吧。

一、几何问题基础知识

1.基础知识：三角形三边关系，即两边之和大于第三边，两边之差小于第三边；三角形周长为三边之和，三角形面积为

2.勾股定理：直角三角形的两条直角边的平方和等于斜边的平方和；常考勾股数有3、4、5，5、12、13，以及成倍数的三边，如6、8、10等。

3.特殊直角三角形及三边比例关系：

二、神奇三角形——直角三角形

同学们读完上面的内容可能会发现，这些知识点很多都和直角三角形有关系。同学们平时复习的时候可能也会发现，很多几何题目是需要求解一些规则或不规则图形的长度、两地之间距离、物体的高度等，而这些却不能直接求出。而这就需要神奇的直角三角形来帮助我们解题，接下来一起去寻找题目中的神奇直角三角形吧。

三、神奇三角形在哪里

【进阶训练】一个半圆形拱门的宽和高分别为8米和4米。一辆货车拉着宽4.8米、每层高20厘米的泡沫板通过该拱门。如果车斗底部与地面的垂直距离为1.1米，问要通过拱门，每次最多可以装载几层泡沫板？（）

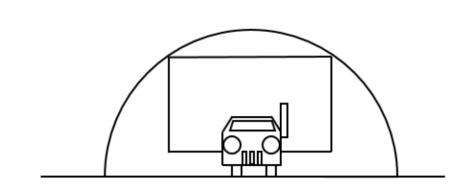
A.9 B.10 C.11 D.12

【答案】B【解析】将原图转化为如下的简易图，当泡沫板的宽正好与拱门接触时，泡沫板的高度和最大，装载泡沫板的数量最多。此时用AB表示泡沫板的宽，O为半圆圆心连接AO，则AO长为4米。过O做OC垂直于AB，垂足为C，则构造了直角三角形AOC，其中AC为AB长度的一半，即2.4米，则根据勾股定理可以求出OC=3.2米。又因为OD=1.1米，则CD=3.2-1.1=2.1米，一层泡沫板高20厘米=0.2米，2.1÷0.2=10.5，所以最多能装载10层泡沫板。故本题选B。

行测数量关系之定位法的应用

概率问题属于行测数量关系中较常考的题型，因此，能够高效拿到这一部分的分对我们来说至关重要。众所周知在古典概率中我们只涉及一个核心公式：在做题的时候我们可以分别把总事件和所求A事件包含的等可能样本数求出来，再代入公式进行求解。说起来简单，但是实际做题的时候大家会发现，计算样本数的时候常常会涉及排列组合的知识点，一下击中了大家的软肋。那怎么样才能避免排列组合，简化做题步骤呢？今天，就给大家带来一个方法：定位法。

定位法什么时候用呢？怎么用呢？我们不妨通过下面题目来一起看看。

【例1】某单位工会组织桥牌比赛，共有8人报名，随机组成4队，每队2人。那么，小王和小李恰好被分在同一队的概率是：（）

【答案】A【解析】题干要求小王和小李被分在同一队，不妨先假设小王已经分好队，剩下7个位置小李可以选择，要想和小王一队，只有一种情况，两人被分在同一队的概率是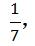故选A。

通过这道题，我们可以知道，当遇到要同时考虑相互联系的元素时(常见的是两个元素有联系)，可以先将其中一个固定，再考虑其他元素的所有可能情况，从而进行求解，这就是定位法。趁热打铁，我们通过下面这题再练一下吧。

【例2】某单位的会议室有5排共40个座位，每排座位数相同。小张、小李随机入座，则他们坐在同一排的概率：（）

A.不高于15% B.高于15%但低于20%

C.正好为20% D.高于20%

【答案】B【解析】若小张固定了座位，剩下39个座位小李可以选，小李要和小张坐在同一排，只能在小张坐的那一排剩余的7个位置上选，故两人坐在同一排的概率是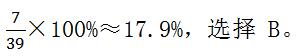

相信通过上面这两道例题大家对定位法已经有了一个很好的认识，但是光认识可不够，还要能够熟练应用到题目中才行，所以平时要多做题哦！