行测数量关系：用好技巧，轻松解决年龄问题

行测年龄问题放心做，学会列表法一招制“题”

必备知识点：1每过n年，每个人年龄增长n岁；2.不论哪年，两人年龄差不变

在解决年龄问题时同学们可以牢牢把握以上两个知识点，通过“列表法”将每个人的各个时间的年龄梳理清楚。结合表格依据年龄差不变可以建立等量关系求解。

例1：3年前张三的年龄是他女儿的17倍，3年后张三的年龄是他女儿的5倍，那么张三的女儿现在：（   ）

A.2岁       B.3岁     C.4岁         D.5岁

【答案】D【解析】根据题目描述，可以设3年前女儿为x岁，则张三为17x岁，3年前和3年后相差6年，每人增长6岁，列表如下，3年前和3年后女儿和张三的年龄如表所示，根据两个时间段年龄差不变可以列等式：17x-x=5(x+6)-(x+6)，解得x=2。所以张三的女儿现在为x+3岁，即5岁。选择D选项。

例2：2020年时，李某的年龄是张某的2/3，且正好是自己工龄的4倍。2024年时，张某的年龄正好是自己工龄的2倍，已知张某参加工作时李某10岁，问李某是几岁参加工作的？（   ）

A.18        B.20     C.22        D.24

【答案】D【解析】根据题目描述，涉及了李某、张某二人的年龄及其工龄，工龄是指从开始参加工作起到当下工作的时间，可以在表格中分别表示。李某年龄是张某的2/3，自己工龄的4倍，可设李某工龄为x，李某年龄为4x，则张某年龄为6x；到2024年，每人年龄工龄都增长4岁，张某年龄是自己工龄2倍，张某工龄为(6x+4)/2=3x+2；已知张某参加工作时李某10岁，也就是说在某年，张某刚参加工作即张某工龄为0时，李某10岁；问题求李某是几岁参加工作的，也就是求其工龄为0时，年龄为多少。观察表格2014年及某年时李某年龄和张某工龄已知，而李某年龄和张某工龄经过n年的变化数值始终相等，可以根据2024年与某年该差值相同列式：(4x+4)-10=(3x+2)-0，解得x=8。从而知道，2020年时，李某工龄8年，年龄32岁。所求的为工龄为0时，年龄为32-8=24岁。选项为D选项。

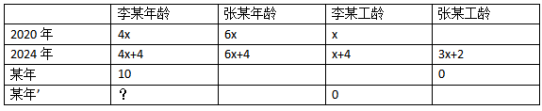
通过以上内容的学习，大家不难发现对于年龄问题可以通过列表将多个人不同时间的年龄梳理清楚。

行测指导：年龄问题你会了吗

数量关系作为行测考查的重要部分，让许多人望而生畏，其实我们只要掌握好几类基础题型，多加练习，便可在数量关系上取得一定优势。年龄问题也是数量关系中经常会出现的一类考题，这类题通常会考查我们两人或者多人之间年龄的关系，对于年龄问题我们应该从何下手，下面就带大家一起学习一下。

一、年龄问题两大原则

在解决年龄问题时，我们要牢记以下两大原则：

1.两人之间的年龄差永远不变

2.每过一年，年龄增加一岁

二、常用方法

方法一：借助年龄差快速解题

在遇到年龄问题时，需要把握住一大核心，就是无论时间如何变化，两人之间的年龄差是固定不变的。

例1：今年姐妹俩年龄和为60岁，若干年前，姐姐的年龄只有妹妹现在这么大时，妹妹的年龄恰好是姐姐年龄的一半，那么妹妹今年多少岁？

A.24      B.30      C.32       D.40

【答案】A【解析】设若干年前，妹妹的年龄是x岁，则姐姐的年龄是2x岁，姐妹俩的年龄差为x岁。则今年，妹妹的年龄是2x岁，姐姐的年龄是3x岁。根据题意有2x+3x=60，解得x=12，所以妹妹今年24岁。故本题选A。

例2：哥哥现在的年龄是妹妹当年年龄的4倍，哥哥当年的年龄是妹妹现在年龄的1.5倍，现在，哥哥与妹妹的年龄和为30岁，则哥哥现在的年龄是多少岁？（   ）

A.18     B.20     C.22       D.24

【答案】B【解析】设妹妹现在年龄为x岁，当年年龄为y岁，则哥哥现在年龄为4y岁，当年年龄为1.5x岁。有4y+x=30，根据年龄差不变可得4y-x=1.5x-y，解得x=10，y=5，则哥哥现在的年龄是20岁。故本题选B。

方法二：借助第二大原则解题

在涉及人数较多，以及多年后的年龄问题时，根据每过一年，所有人年龄增加一岁来找年龄之间的关系。

例3：2020年小华的父母年龄之和是小华的6倍，四年后小华的父母年龄之和是小华的5倍。已知小华的父亲比他的母亲大2岁，那么2020年小华父亲多少岁？（   ）

A.35       B.37      C.40       D.42

【答案】B【解析】设小华2020年的年龄X岁。

根据“四年后小华的父母年龄之和是小明的5倍”得等量关系6x+8=5(x+4)，解得x=12，2020年小华父母的年龄和为72岁，则所求为(72+2)÷2=37岁，故本题选择B。

通过前面的三道例题带大家了解什么是年龄问题，以及如何解决此类题型，对于数量关系我们还是需要多练习熟悉，万事功到自然成。

行测数量关系难点——年龄问题

年龄问题在国考、省考或事业单位的行测考试中，都属于有可能会被考查的一类问题，很多考生在学习的过程中可能会认为，年龄问题题目所给数据较为混乱，不易梳理，导致缺少解题思路。今天带着大家学习年龄问题的解题原则，了解年龄问题的做题方法。

解题原则

①每个人每过一年年龄增长一岁；

②任意两人的年龄差不会改变。

解题方法

①通过列表梳理已知条件；

②根据题干中明显的等量关系列方程求解；

③如题干中无明显的等量关系描述，可根据年龄差不变构造等量关系列方程求解。

例1：一个三口之家，爸爸比妈妈大3岁，现在他们一家人的年龄之和是80岁，10年前全家人的年龄之和是51岁，则女儿今年多少岁？（   ）

A.7       B.8       C.9          D.10

【答案】C【解析】正常情况下，10年前一家三口的年龄之和为80-3×10=50岁，而现在是51岁，说明女儿10年前没有出生，则女儿今年是10-(51-50)=9岁。

例2：2018年父亲年龄是女儿年龄的6倍，是母亲年龄的1.2倍。已知女儿出生当年(按0岁计算)母亲24岁，则哪一年父母年龄之和是女儿的4倍？（   ）

A.2036       B.2039      C.2042         D.2042

【答案】B【解析】根据题意知父亲、女儿、母亲的年龄之比为6∶1∶5，母亲的年龄比女儿大4份，对应24岁，则一份对应6岁，因此2018年父亲、女儿、母亲的年龄分别为36岁、6岁、30岁。设经过x年后，父母年龄之和是女儿年龄的4倍，则有36+30+2x=4×(6+x)，解得x=21，故在2018+21=2039年，父母年龄之和是女儿年龄的4倍。

例3：甲乙两人年龄不等，已知当甲像乙现在这么大时，乙8岁；当乙像甲现在这么大时，甲29岁。问今年甲的年龄为多少岁？（   ）

A.22        B.34      C.36         D.43

【答案】A【解析】设甲今年x岁，乙今年y岁，列表如下：

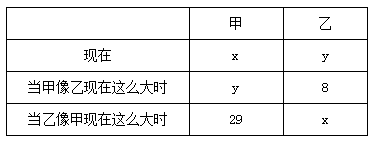
根据年龄差不变，有x-y=y-8=29-x，解得x=22，故今年甲的年龄为22岁，选A。

总结

年龄问题主要抓住年龄差不变的原则，利用年龄差构建等量关系并列方程求解。相信大家通过一定的练习，一定能够掌握解决此类问题的方法，在考试中快速地选出正确答案。

只要列表用得好行测年龄问题没烦恼

行测考试时间紧，数量关系难度大，数量题目重点在于题干梳理和计算。如果某种类型做题方法和思维方式较统一，那这类型题就是我们应该重点攻克的题型，以增加考试时可选的题目数和提高得分的可能性。今天为大家介绍的年龄问题就有这样的特征。

题型特征

题干中涉及多种时间状态下，多个人之间年龄的变化的问题。

解题关键

(1)不管经过多少年，两人之间的年龄差不变。(如：今年姐姐比妹妹大3岁，5年后姐姐比妹妹仍大3岁)

(2)经历过相同的年份，年份差不变，即每个人的年龄变化相同。(如：今年姐姐28，妹妹23；3年后，姐姐31，妹妹26；姐姐年龄变化了3岁，妹妹年龄也变化了3岁)

我们在做题时，可通过表格梳理每种状态下各个人的年龄，利用以上两个结论或题干中的等量关系，设未知数列方程求解。

例题：(1)小明和爷爷在做数学游戏，小明说：“我比弟弟大10岁，而且我比爷爷小我年龄的4倍”，爷爷和小明年龄的总和是弟弟年龄的18倍，问爷爷与弟弟年龄之和比小明年龄大多少岁？（   ）

A.65        B.60      C.62       D.58

【解析】答案选A。根据题意，设未知数并列表如下：

由题目条件可设小明的年龄为x岁，其弟弟为(x-10)岁，爷爷为5x岁，“爷爷和小明年龄的总和是弟弟年龄的18倍”可列式子x+5x=18(x-10)，解得x=15岁，故爷爷年龄为75岁，弟弟年龄为5岁，所求为75+5-15=65岁。

例题：(2)甲、乙、丙三人现在的年龄和是113岁，当甲的岁数是乙的岁数的一半时，丙是38岁；当乙的岁数是丙的岁数的一半时，甲是17岁。那么乙现在是多少岁？

A.30          B.32       C.35        D.36

【答案】B【解析】根据题意，设未知数并列表如下：

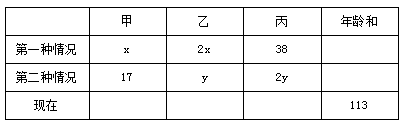
根据年龄差不变，列方程得2x-x=y-17，38-2x=2y-y；解得x=7，y=24。则可知甲、乙的年龄差为7岁，乙、丙的年龄差为24岁，设乙现在的岁数为z，则甲、丙现在的年龄分别为(z-7)岁、(z+24)岁，则(z-7)+z+(z+24)=113，解得z=32，故本题选择B。

希望大家认真学习用好列表方法，通过列表梳理复杂条件，结合题干中等量关系或两个结论(年龄差不变、年份差不变)来解题，真正掌握该问题的解决技巧！

行测数量关系：构造等量关系解决年龄问题

在行测考试中，数量关系中包含的题型种类繁多，让人眼花缭乱，大部分同学都是选择一部分相对比较容易的题目来做。其中，年龄问题的题目易于理解，解题方法好掌握，是同学们容易上手的一类题目。今天就带领大家来解决年龄问题。

解题核心

1.年龄差不变

例如：小王今年20岁，小李今年25岁，今年两人相差5岁，10年后两人依然相差5岁。

2.年龄同增同减

例如：弟弟今年8岁，哥哥今年10岁，5年后，兄弟两人年龄都增加5岁，5年前兄弟两人年龄都减少5岁。

方法应用

1.结合题干描述，列表梳理题干信息。

2.利用年龄差不变构造等量关系。

3.通过年龄同增同减，结合题干条件构造等量关系。

例1：爸爸、哥哥、妹妹现在的年龄和是64岁。当爸爸的年龄是哥哥的3倍时，妹妹是9岁；当哥哥的年龄是妹妹的2倍时，爸爸34岁。现在爸爸的年龄是多少岁？（   ）

A.34       B.39         C.40       D.42

【答案】C【解析】当妹妹9岁时，设哥哥的年龄为x岁，则爸爸的年龄为3x岁；当爸爸34岁时，设妹妹的年龄为y岁，则哥哥的年龄为2y岁。列表如下：

根据年龄差不变，可得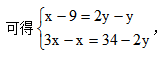解得x=13，则妹妹9岁时，哥哥年龄为13岁，爸爸年龄为3×13=39岁，三人年龄和为9+13+39=61岁，现在三人年龄和64岁，现在距离妹妹9岁时过了(64-61)÷3=1年，则现在爸爸的年龄是39+1=40岁。故本题选C。

例2：3年前张三的年龄是他女儿的17倍，3年后张三的年龄是他女儿的5倍，那么张三的女儿现在多少岁？（   ）

A.2岁     B.3岁      C.4岁      D.5岁

【答案】D【解析】设女儿现在的年龄为x岁，列表如下：

根据年龄差不变，有17×(x-3)-(x-3)=5×(x+3)-(x+3)，解得x=5，则女儿现在的年龄为5岁。故本题选D。

年龄问题是一种相对来说比较容易理解掌握的题型，通过表格形式梳理题干，结合年龄差不变构造等量关系，即可轻松解题。希望大家能够多加练习，这样我们就能更好地解决这类题目。

行测年龄问题，你必须要掌握的两个点

在行测考试数量关系的题目中，年龄问题出现概率还算比较高，虽然该题型整体难度不大，掌握方法后求解也不复杂，相对容易得分，但总是有很多同学在考试中遇到的时候依然失分，非常可惜。其实，同学们如果掌握了这类题型的解题原则和解题思路这两个点，基本上就是十拿九稳，拿分可算是易如反掌。接下来就跟大家聊一聊年龄问题。

解题原则

1.每个人的年龄是同时增加的，而且增加量都相同。比如，甲的年龄增加了3岁，那乙的年龄也增长了3岁。

2.同一时刻，任意两人的年龄差不变。比如，甲的年龄比乙大3岁，那5年后，甲的年龄比乙还是大3岁。

解题思路

年龄问题题干相对好理解，但往往涉及多个主体、多个时间的年龄关系，容易混淆。在解决此类问题时，建议先列表梳理题干信息，再根据题中明显的等量关系列方程求解。整体来看，解题思路就是“列表+方程”，我们通过以下三道题目来给大家说明。

例1：办公室有甲、乙、丙、丁4位同志，甲比乙大5岁，丙比丁大2岁。丁三年前参加工作，当时22岁。他们四人现在的年龄之和为127岁，那么乙现在的年龄是多少岁？（   ）

A.25岁       B.27岁       C.35岁       D.40岁

【答案】C【解析】根据丁三年前22岁，可知丁现在25岁。由丙比丁大2两岁，可知丙现在27岁。设乙现在的年龄为x岁，则甲现在年龄为(x+5)岁。四人的年龄列表如下：

根据“他们四人现在的年龄之和为127岁”，有x+5+x+27+25=127，解得x=35。选择C选项。

例2：小李的弟弟比小李小2岁，小王的哥哥比小王大2岁、比小李大5岁。1994年，小李的弟弟和小王的年龄之和为15。问2014年小李和小王的年龄分别为多少岁？（   ）

A.25，32        B.27，30     C.30，27       D.32，25

【答案】B【解析】设1994年小李的年龄为x岁，则四人在1994年的年龄列表如下：

根据“在1994年，小李的弟弟和小王的年龄之和为15”，有x-2+x+3=15，解得x=7。进而可知1994年和2014年四人的年龄情况：

由表可知，2014年小李和小王的年龄分别为27岁和30岁。选择B选项。

例3：3年前张三的年龄是他女儿的17倍，3年后张三的年龄是他女儿的5倍，那么张三的女儿现在多少岁？（   ）

A.2岁        B.3岁       C.4岁       D.5岁

【答案】D【解析】设三年前张三女儿的年龄为x岁，则张三和他女儿的年龄列表如下：

根据“3年后张三的年龄是他女儿的5倍”，有17x+6=5×(x+6)，解得x=2，故女儿现在的年龄为x+3=5岁。选择D选项。

年龄问题的解题原则和解题思路，大家是否都记住了呢？记住“列表+方程”哦，祝大家取得好成绩！