数量关系易混淆知识点及必考考点速记

数量关系易混淆的知识点

今天给大家解决一对易混淆的知识点——平均数增长率的计算和两期比重差值计算。

1.两期比重差值计算

题目特征：题目中出现“……占……比重同比/与上年同期相比上升/下降（百分点或%）”

做题方法：按照先判断升降，再求解相差多少百分点（%）的顺序做题，最后套入两期比重差值公式A/Bx（a-b）/(1+a)

2.平均数增长率计算

题目特征：题目中同时出现“均、每、单位”此类平均数特征词汇以及增长率题目特征“增长/减少（%）”

做题方法：直接找到总数和总个数对应增长率，代入平均数增长率公式求解即可，（a-b）/(1+b)

各位小伙伴一定要牢记题型特征同时注意区分公式，避免混淆。接下来以两道典型题目为例熟练相应做题技巧。

【例1】2017年全国海洋生产总值77611亿元，比上年增长6.9%，海洋生产总值占国内生产总值的9.4%。

2017年，J省海洋生产总值为7217亿元，比上年增长9.2%，海洋生产总值占地区生产总值的8.4%，2017年，全省沿海沿江港口完成货物吞吐量20.4亿吨，同比增长8.3%；集装箱吞吐量1698.8万标箱，同比增长5.5%。

2017年J省海洋生产总值占全国的比重比上年：（   ）

A.上升了约0.2个百分点

B.上升了约2个百分点

C.下降了约0.2个百分点

D.下降了约2个百分点

【答案】A【解析】第一步，本题考查两期比重计算问题。

第二步，定位文字材料第一、二段，“2017年全国海洋生产总值77611亿元，比上年增长6.9%，J省海洋生产总值为7217亿元，比上年增长9.2%”。

第三步，解法一：

根据部分增长率9.2%＞整体增长率6.9%，比重上升，排除C、D选项，根据两期比重差＜|9.2%-6.9%|=2.3%，A、B选项均成立，但是部分量远小于整体量，则两期比重差远小于2.3%，答案为A选项。

解法二：代入两期比重差公式：

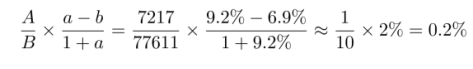
即上升了0.2个百分点。

【例2】2011年，我国规模以上电子信息制造企业主营业务成本占主营业务收入的比重达到88.7%，比2010年提高0.6个百分点，行业中亏损企业2497个，同比增长36.7%，企业亏损面达16.6%，亏损企业亏损额同比增长52.9%。

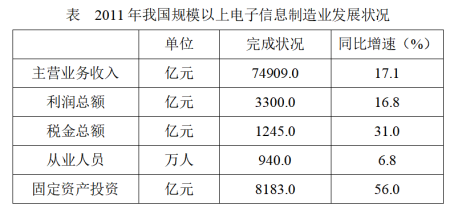
2011年，我国规模以上电子信息制造业人均创造利润约比上年增加：（   ）

A.9%

B.11%

C.15%

D.17%

【答案】A【解析】第一步，由问题“人均创造利润约比上年增加%”，判定本题考查平均数的增长率。

第二步，定位表。

第三步，“利润总额增长率为16.8%，从业人员为6.8%。”代入平均数增长率计算公式(a-b)/(1+b)=(16.8%-6.8%)/(1+6.8%)＜10%，故2011年，我国规模以上电子信息制造业人均创造利润约比上年增加9%。

因此，选择A选项。

以上，希望各位小伙伴们能够通过上面两道例题的讲解，区分清楚平均数增长率和两期比重差值计算题目的特征，同时熟练运用公式快速解决此类题目。

数量关系中的时间问题你都会了吗

【基础知识】

1.平年闰年判定，具体判定方法如下：

首先判定是否为世纪年：世纪年指年份末两位为00的年份。世纪年整除400为闰年，如：1900不能被400整除，是平年，所以闰年包括世纪闰年和普通闰年两种划分，而非世纪年整除4为闰年。（闰年366天、平年365天）

2.大月份、小月份、特殊月

(1)大月份：有31天的月份，分别为：1月、3月、5月、7月、8月、10月、12月。

(2)小月份：有30天的月份，分别为：4月、6月、9月、11月。

(3)特殊月：2月份，闰年的2月有29天，平年的2月有28天。

3.每过一年的同一日期，平年星期加1(共365天，365÷7=52……1，故往后推一天)，闰年星期加2(共366天，366÷7=52……2，故往后推两天)。

4.年龄问题

（1）两人的年龄差不变；

（2）每过N年，每人都长N岁；

方法：代入排除法、方程法。

5.①每昼夜24小时，每小时60分钟，每分钟60秒。

②一个指针走完一圈为360度，一个表盘360度；总共分为12大格（小时）和60个小格（分钟）；1个大格等于30度，一个小格等于6度。

③时针每分钟走0.5度，分针每分钟走6度，速度差为5.5度/分，速度之比1：12。

④时针分针特殊夹角

a、直角：每小时2次，每昼夜44次（3点、9点、15点、21点因重复计算所以减去）

b、重合：每小时1次，每昼夜22次（12点、24点因重复计算所以减去）

c、180度角：每小时1次，每昼夜22次（6点、18点因重复计算所以减去）

【经典例题】

【答案】A【解析】第一步，本题考查星期日期问题。

第二步，2021年1月9日跟2020年1月9日相比，因为2020年2月为闰月，所以2021年1月9日星期+2，为星期六。因为1月为大月，所以2021年1月9日到2021年2月9日经过了31天，31÷7=4……3，星期+3为星期二。

因此，选择A选项。

【答案】D【解析】第一步，本题考查年龄问题。

第二步，设3年后，张的年龄为x岁，则王的年龄为3x-2，再过5年，张为x+5，王为3x+3，根据王比张的2倍多5岁列方程：3x+3=2（x+5）+5，解得x=12，此时王的年龄为39岁，在此基础上过10年，王的年龄是39+10=49岁。

因此，选择D选项。

【答案】B【解析】第一步，本题考查钟表问题。

第二步，3点时，分针落后时针90°，经过19分钟，分针比时针多走19×（6°－0.5°）＝104.5°，故3点19分所构成的锐角为104.5°－90°＝14.5°。因此，选择B选项。

数量关系6大必考点速记

★第一记：经济利润问题

1.总售价=单价×销售量

2.利润=售价-成本；总利润=总售价-总成本；总利润=单件利润×销售量

3.利润率=利润成本=售价-成本成本=售价成本-1

4.注意：打折是在定价或者售价的基础上打折，而不是直接在成本上打折

★第二记：行程问题

1.核心公式：路程=速度×时间(s=v×t)(单位换算：1m/s=3.6km/h)

2.等距离平均速度：v-=2v1v2v1+v2

3.火车过桥问题：

火车完全过桥路程=桥长+车长火车完全在桥上路程=桥长-车长

4.相遇追及问题主要考查两端(或单端)出发的相遇(或追及)时，各个量之间的逻辑关系。

直线相遇：S和=(V1+V2)t相遇

直线追及：S差=(V1-V2)t追及

环形相遇：nS=(V1+V2)t相遇(反向运动)

环形追及：nS=(V1-V2)t追及(同向运动)5.流水行船问题：S顺=(V船+V水)×t顺，S逆=(V船-V水)×t逆

★第三记：工程问题

一、工程问题核心公式工作总量=工作时间×工作效率

二、基本工程问题解题思路

1.给定时间型：题目只给出时间，可以赋值工作总量为给出时间的最小公倍数，然后再结合各个时间，求出每个主体的效率，再进行解题。2.效率制约型：给出效率之间的制约关系，可赋值各个主体的效率为最简效率比，然后求出工作总量，再进行解题。3.条件综合型：当题目已知工作量、效率、时间中两个量的具体数值时，结合题意找到几个量的前后变化，根据公式列式或结合方程求解。

★第四记：几何问题

一、常用公式

1.常用周长公式正方形周长C正方形=4a；长方形周长C长方形=2(a+b)；圆形周长C圆=2πR 2.常用面积公式正方形面积S正方形=a2；长方形面积S长方形=ab；

三角形面积S三角形=1 2 ah；平行四边形面积S平行四边形=ah；

梯形面积S梯形=1 2(a+b)h；扇形面积S扇形=n°360°πR2

3.常用表面积公式正方体的表面积=6a2；长方体的表面积=2ab+2bc+2ac；

圆柱的表面积=2πRh+2πR2，侧面积=2πRh；球的表面积=4πR2

4.常用体积公式正方体的体积=a3；长方体的体积=abc；球的体积=4 3πR3；

圆柱的体积=πR2h；圆锥(棱锥)的体积=1 3×底面积×高

二、几何图形比例关系：

1.若将一个图形尺度变为原来的N倍，则：对应角度不变；对应周长变为原来的N倍；面积变为原来的N2倍；体积变为原来的N3倍。

2.三角形不等性质在三角形中，两边之和大于第三边，两边之差小于第三边。

★第五记：排列组合问题

(一)排列：从m个不同元素中任取n个，排成一列。

组合：从m个不同元素中任取n个，并成一组。

排列与组合的区别：前者与顺序有关，后者与顺序无关。(二)特殊模型

(1)捆绑法：题型标志：必须相邻、必须相连、不能分开解题方法：先整体后内部

(2)插空法：题型标志：不能相邻、不能相连、必须分开解题方法：将不能相连的元素插入无要求的元素中

(3)隔板法：

题型标志：分东西(东西是相同的)、至少分1个解题方法：将n个相同的东西分给m个人，每人至少分1个，有Cm-1 n-1种分法。(4)错位排列题型标志：N个人对应n个位置，每个人都不能回自己的位置解题方法：D1=0，D2=1，D3=2，D4=9，D5=44，D6=265，……

★第六记：概率问题

1.概率=满足条件的情况数÷总数

2.分类概率用加法，分步概率用乘法

3.逆向思维：特定情况的概率=1-反面情况的概率