
行测指导:常见题型之行程工程问题
你是否被“走路”所困惑
行程问题是与我们生活息息相关的一类问题,同时也是行测考试中的高频考点。这类题目考查方向还挺广,无论怎么考查都是在基础上的变型,接下来帮大家打打根基。
直击要点
这类题型研究的核心其实只有一个:“路程=速度×时间”。考察基础公式的同时,也有可能考察来回折返、多主体一起运动等考点,以此来增加试题的难度和复杂程度,但是只要掌握的核心公式,这类题目都不难。
解题法宝
利用行程图+方程来解决此类问题。绘制行程图时注意:
(1)根据题干表述逐句画图,标明这一段的已知量,涉及多个主体可以用虚实线区分。
(2)寻找图像中路程(即相等的线段)的等量关系,从而根据“路程=速度×时间”公式列式。
例题分析
例一
基础公式
某人骑自行车从甲地到乙地,他从甲地出发,用20分钟行完全程的五分之二,然后每分钟比原来多行60米,15分钟的行程和前面一样多,甲乙两地相距多少千米?( )
A.12 B.10.8 C.10 D.9
【答案】D【解析】1、通过题干得知,通过两种不同的速度所走的路程是相等的,所以可以根据路程相等去构建等量关系。
2、题干中两次速度的对比只是给了二者关系没有具体数据,所以可以设原来速度为v米/分,则此时速度为v+60米/分。
3、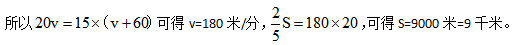
例二
来回折返结合图像快速求解
小明的步行速度为1米/秒,从A到B地步行需要3小时,骑自行车需要1小时,电动车的速度是自行车速度的两倍,现在小明从A地出发,步行1.5小时后骑自行车到B地,然后返回途中先骑电动车走完一半路程,再步行返回A地,则小明往返A、B两地共用多少小时?( )
A.3.75 B.4 C.4.25 D.4.5
【答案】A【解析】

2、可以借助行程图可以快速分析:因为所求为时间可以之间分析时间
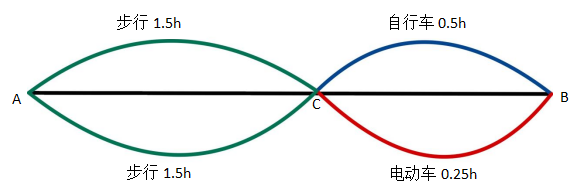
通过观察可以快速得到共用时3.75小时。
例三
多主体基本行程问题
小赵骑车去医院看病,父亲在发现小赵没有带医保卡时以60km/h的速度开车追上小赵,把医保卡交给他并立即返回。小赵拿到医保卡后又骑了10分钟到达医院,小赵父亲也同时到家。假如小赵从家到医院一共用时50分钟,则小赵的速度为多少km/h?( )(假定小赵及其父亲全程都匀速行驶,忽略父子二人交接卡的时间)
A.10 B.12 C.15 D.20
【答案】C【解析】1、画图梳理题干信息
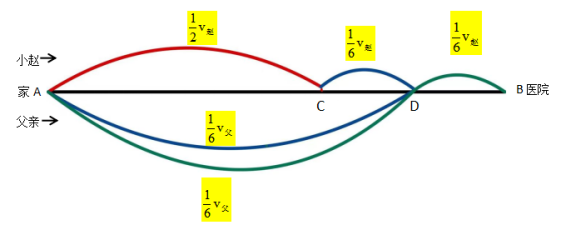
2、根据行程图中的等量关系列式计算
建议大家可以通过这几个题目加深对基础公式的理解和应用,日后多加练习,让这类题目成为势在必得之题。
带你理清流水行船
行程问题研究的是物体运动过程中路程、速度和时间三者之间的关系,是公职考试中的高频题型。其中涉及基本行程、相遇追及、二次相遇、牛吃草问题、流水行船问题,在本文研究的就是流水行船问题。想要求解这类问题,可以首先从生活的角度切入理解问题本质,其次记住主要公式,最后通过画行程图、代入基本公式、列方程等方式求解。
基本公式
相信大家在生活中都骑过自行车,试想你喜欢在大风中骑车吗?答案不一定,如果顺着风就喜欢,逆着风就不喜欢。因为顺风骑车时除自己本身速度,还有风速助推,即顺风骑车速度=自身速度+风速;而逆风骑车时达不到自己本身速度,因为有风速阻碍,即逆风骑车速度=自身速度—风速。

公式应用
例1:一艘货船从上游A码头运货到下游B码头后返回,已知A、B两码头相距240千米,货船在静水中的速度是20千米/小时,水流的速度是4千米/小时。往返共用多少小时?( )
A.15 B.25 C.35 D.45
【答案】B【解析】货船从A到B的顺水速度是20+4=24千米/小时,顺水行驶时间为240÷24=10小时;货船从B到A的逆水速度是20-4=16千米/小时,逆水行驶时间为240÷16=15小时.则往返共用了25小时。选择B项。
例2:A、B两港相距240千米,一艘轮船从A港出发顺流而下,用了6小时到达B港。若静水中轮船的速度为36千米/小时,则这艘轮船从B逆流而上到A港需要多长时间?( )
A.6.5 B.7 C.7.5 D.8
【答案】C【解析】由题可得,该轮船顺水速度为240÷6=40小时/千米,则水速为40-36=4千米/小时,因此轮船逆水的速度为36-4=32千米/小时,故逆流而上需要240÷32=7.5小时。
行测行程工程做的慢?巧用比例帮你算
在行测数量关系中行程问题和工程问题一直是高频考点,但是考试时间有限,很多时候明明是同学们会做的题型却没有时间做,所以掌握一些高频考点的解题技巧非常重要,今天就来跟大家分享一种行程和工程问题通用的一种能解题技巧——正反比。
应用正反比需要满足一定的条件:满足M=A×B的关系,且存在不变量,接下来我们分别来说一下:
工程问题
工程问题的核心公式是W=P×t,满足了M=A×B的关系。当W一定时(不变量),P和t反向变化,成反比;当P一定时,W和t同向变化,成正比;当t一定时,W和P同向变化,成正比。在解题时,我们要抓住题干信息中存在的不变量才可以用正反比,接下来我们结合一道题来看一看怎么应用。
例题:某工厂要在规定时间内生产一批玩具,如果每天生产120个刚好在规定时间完成;如果每天生产140个,能提前两天完成,问这批零件共有多少个?
读完这道题很明显为一个工程问题,通过题干我们能提炼出无论每天生产120个还是140个,这项工程的工作总量都是不变的,W一定,P之比为6:7,所以t与P成反比,为7:6,原来的时间为7份、提高之后为6份,提前了一份,对应提前的2天,则原来的7份对应14天,每天生产120个,所以W=14×120=1680个。
行程问题
行程问题公式为s=v×t,满足了M=A×B的关系。当s一定时,v和t成反比;当v一定时,s和t成正比;当t一定时,s和v成正比。
例题
小强每天早上从家开车到公司上班,如果以正常速度行驶需要1小时到达,如果速度提升25%,可以提前多少分钟到达?
这道题目是一个行程问题,无论车速提升与否行驶的路程是不变的。s一定,v之比为4:5,则t之比为5:4,没提速前需要1小时也就是60分钟到达,5份对应60分钟,1份对应12分钟,问提前多少分钟到达,提前了1份的时间,所以可提前12分钟到达。
最后我们来加一下难度,看一下这道题:
例题
一架战斗机从甲机场匀速开往乙机场,如果速度提高25%,可比原定时间提前12分钟到达,如果以原定速度飞行600千米后,再将速度提高三分之一,可以提前5分钟到达,那么甲乙两机场的距离是多少千米?
这道题是一道行程问题。无论速度如何变化,总路程都是从甲到乙的距离,是不变的。s一定,由速度提高25%可知,原定速度和第一次提速后的v之比为4:5,则t之比为5:4,时间上少一份对应提前12分钟,所以原定时间为5份,对应60分钟;如果以原定速度飞行600千米后,再将速度提高1/3,则600千米后的路程一定,原定速度与第二次提速后的速度之比为3:4,则时间之比为4:3,时间少一份,对应提前5分钟,所以600千米后的路程,原定时间应走20分钟,则可求600千米按原定速度所用的时间为60-20=40分钟=2/3小时,进而可以求出原定速度为600÷2/3=900千米/时,则甲、乙两机场的距离为900×1=900千米。








