行测数量关系快速解题技巧
整除帮你快速解题
关于行测数量关系题，只要用对方法是可以快速选出正确选项的，其中有一种方法就是利用整除的思维，所以，今天带领大家了解并掌握如何利用整除快速解题。
一、整除的概念
若a÷b=c(a、b、c均为整数)，则a能被b整除。
二、整除关系的确定
在做题过程中，大部分题目涉及的数据都是整数，这个时候就可以考虑用整除解题了。什么时候确定可以用整除呢？这就需要我们对一些关键信息敏感一些。
1、文字描述：题干中出现“整除、平均、每、倍”等字眼时，一般存在整除关系。
例1：某班级发放课外书，平均每人能分到7本。后来该班级又转来若干学生，这样每人能分到6本，该班级课外书总数是（ ）。
A.180本 B.210本 C.240本 D.280本
【答案】B【解析】题干中出现了“平均每”这样的字眼，考虑用整除。由题意可知，课外书总数=7×班级原人数=6×班级现人数，则课外书总数能被7和6整除，选项中只有B符合。
2、特征数据：题干出现“分数、百分数、比例”等特征数据时一般也存在整除关系。
例2：学校有足球和篮球的数量比为8∶7，先买进若干个足球，这时足球与篮球的比变为3∶2，接着又买进一些篮球，这时足球与篮球数量比变为7∶6，已知买进的篮球比买进的足球多3个，原来足球有多少个（ ）？
A.48 B.42 C.36 D.30
【答案】A【解析】题干中出现了比例，考虑用整除。题目求的是原来的足球有多少个，在题干中，已知学校原有足球和篮球的数量比是8∶7，可以确定原来的足球数量能被8整除，排除B、C、D，只有A符合条件。
三、学以致用
相信同学们对整除的概念和用法都有所了解了，接下来再来看一道题目，大家可以尝试用不同的方法解题，通过对比进一步感知整除的快捷。
例3：若干学生住若干房间，如果每间住4人，则有20人没地方住，如果每间住8人，则有一间房只有4人住，问共有多少学生？
A.30 B.34 C.40 D.44
【答案】D【解析】方法一：根据题干可知，两种安排方案中学生人数是不变的，可围绕着学生人数构造等量关系。设房间数为x，得到4x+20=8(x-1)+4，求得x=6，进而得到学生人数为4×6+20=44人，选D。
方法二：题干中出现“每”字眼，考虑用整除。根据每间住4人，则有20人没地方住可知，学生人数减20能被4整除，20能被4整除，即人数能被4整除。排除A、B选项。根据每间住8人，则有一间房只有4人住可知，学生人数减4能被8整除，只有D符合条件。
通过不同解题方法的对比，整除的方法是不是更加方便快捷？同学们快点运用起来吧。
浅谈行测数量关系中的比较构造法
在公务员考试中，行测中的数量关系的题型是大家比较头痛的，也是大家比较想放弃的，我们要做到的是在考试中尽可能快速地选择几道数量关系的题目来做。选择什么样的题目就尤为重要了，同样在快速求解的时候利用什么方法也很重要，下面给大家讲解数量关系中常见的应用方法——比较构造法。
一、含义
比较构造法指的是对同一件事有两种或两种以上完成方案，通过比较方案间的差异，从而构造等量关系求解的方法。我们一起来看个例子。
例1：某车队运输一批蔬菜。如果每辆汽车运3500千克，那么还剩下5000千克；如果每辆汽车运4000千克，那么还剩下500千克，则该车队有（ ）辆汽车。
A.8 B.9 C.10 D.11
【答案】B【解析】根据题意，有两种运输方案，可对比两种方案的差异进行求解。
对比两种方案可知，每辆车要是多运输500千克，总共能多运输4500千克，所以共有(5000-500)÷(4000-3500)=9辆车。由选项可知，本题选择B项。
二、比较构造法的应用
例2：有一批汽车零件由A和B负责加工，A每天比B少做3个零件。如果A和B两人合作需要18天才能完成，现在让A先做12天，然后B再做17天，还剩这批零件的1/6没有完成，这批零件共有多少个？（ ）
A.240 B.250 C.270 D.300
【答案】C【解析】已知A和B合作需要18天才能完成，那么A和B合作完成5/6的零件需要18×5/6=15天。若以完成5/6工作量的时间进行分析可得：
A做3天的工作量=B做2天的工作量，所以PA：PB=2：3，已知A每天比B少做3个零件，所以一份等于3，可得A和B每天共做(2+3)×3=15个零件。所以这批零件共有15×18=270个。由选项可知，本题选择C项。
通过上述题目希望大家对于比较构造法有一定的了解与认识，所谓比较构造就是我们要对比方案间的差异，来构建等量关系求解。同时依然需要大家在以后的备考中能够应用到相应的题目中，提高解题速度。
正反比——行测数学运算解题小妙招
工程、行程问题作为行测考试中的常见题型，除了可以应用方程法求解，还有一种比较简便的方法——正反比。正反比相对于常见的方程求解，其最大的优势在于简化计算量，降低了计算难度，可以很大程度上帮助我们快速得出答案。在此进行展开分析。
一、正反比的应用环境
在行程问题中，路程=速度×时间；工程问题中，工作总量=工作效率×时间，两者的公式本质上都是M=A×B的形式。当A为定值，M与B成正比关系；B为定值，M与A成正比关系；当M为定值，A与B成反比关系。所以，只要在M=A×B的模型中，满足三个量中某一个量为定值，就可以用正反比关系来解题了。
二、正反比的应用
例1：一架战斗机从甲机场匀速开往乙机场，如果速度提高25%，可比原定时间提前12分钟到达；如果以原定速度飞行600千米后，再将速度提高1/3，可以提前5分钟到达。那么甲、乙两机场的距离是多少千米？（ ）
A.750 B.800 C.900 D.1000
【答案】C【解析】方法一，利用方程求解，设原速为v千米/小时，原定时间为t小时，则根据路程一定可得，v×t=(1+25%)v×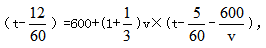
解得t=1，v=900，则总路程为900×1=900千米。
方法二，路程一定，利用正反比求解，速度提高25%后，速度之比为4：5，原定时间与所需时间的比为5：4，差1份，对应12分钟，则原定时间为12×5=60分钟。飞行600千米后的剩余路程，速度之比为3：4，原定时间与所需时间的比为4：3，，差1份，对应5分钟，则剩余路程的原定时间为4×5=20分钟，故飞行600千米所用时间为60-20=40分钟，则甲、乙两机场的距离为600÷40×60=900千米。
例2：某工厂计划在一定时间内生产一批计算机，如果每天生产140台，可提前3天完成，如果每天生产120台，则要再生产3天才能完成，问规定完成的时间是多少天？（ ）
A.30 B.33 C.36 D.39
【答案】D【解析】方法一，利用方程求解，两者方式工作总量不变，设规定完成的时间为t天。总量=140×(t-3)=120×(t+3)，解得t=39。
方法二，利用正反比求解，计算机的总量不变，效率的比值为140：120=7：6，则时间的比值为6：7，时间的比例上相差一份，具体时间相差6天，1份对应6天，则按照140台的效率去算，6份对应36天，提前3天完成，因此原计划39天，选择D。
通多对比以上两道题目的不同解题方式可以发现，方程法列式更为直观，但解题的计算量比较大，而正反比的方法更侧重于思维方式的转变，计算难度较低，可以极大地节省时间。
行测数量关系：找到“最不利”，方可无往而不利
成功学理论告诉我们，一个人如果想要成功，必得经受最不利的形势，才能触底反弹，收获成功，对于这个成功学的逻辑，不仅适用于工作，也适合解决行测数量关系中的一类问题，这类问题需要找到最不利情况后再求解。具体来看看下边的题目。
例题：一个暗箱中有同样大小，同样质地的黑球和白球各5个。问至少从箱子中拿出多少个球才能保证拿到白球？
【解析】此题问法中有两个要求，一是最少，二是保证。要保证拿到白球，就需要考虑最不利情况，也就是与拿到白球一线之差的情况，成功就是拿到白球，对于此题，最不利的情况就是将黑球全都拿出来，此时再拿1个球，拿出的一定是白球，即保证拿到白球，且满足题干要求的最少。因此，至少需要拿出5+1=6个球才能保证拿到白球。
【点拨】
此类题目的题型特征为题干中出现“至少……才能保证(就一定)”的表述；
解题原则为最不利原则，在取的过程中尽量先让结果不发生，即与成功一线之差。
结果的计算为最不利情况数加1。
接下来通过例题来感受下如何使用最不利原则求解题。
例1：某高校举办的一次读书会共有38位学生报名参加，其中中文、历史、哲学专业各有10位学生报名参加了此次读书会，另外还有4位化学专业学生和4位物理专业的学生也报名参加了此次读书会，那么一次至少选出（ ）位学生，将能保证选出的学生中至少有5位学生是同一专业的。
A.17 B.20 C.21 D.39
【答案】C【解析】题目问“至少……才能保证”，符合最不利原则解决的问题特征。利用最不利原则可知，“至少有5位学生是同一专业”的最不利的情况是“4位同学是同一专业”，先选出中文、历史、哲学、物理以及化学专业的学生各4位，此时若再选出1位学生就可以保证至少有5位学生是同一专业的，因此共选出4×5+1=21位，选择C项。
例2：有四种颜色的文件夹若干，每人可取1-2个，至少有几人去取，才能保证有3人所取到的文件夹完全相同？（ ）
A.20 B.21 C.28 D.29
【答案】D【解析】由题可知，题目问“至少……才能保证”，符合最不利原则解决的问题特征。根据题意可知，取1个文件夹时，则有4种情况；取2个文件夹时，如果两个文件夹颜色相同，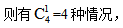
如果两个文件夹颜色不同，
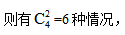因此取出的文件夹共有4+4+6=14种情况。利用最不利原则可知，“3人取到的文件夹完全相同”的最不利情况是“每种文件情况都有2人取到”，那么此时再来1个人，就一定保证有3人取得的文件夹情况完全相同，因此至少要有14×2+1=29个人，选择D项。
【点拨】当最不利情况数不明确时，需要结合排列组合求出所有情况总数，再利用最不利情况数+1求解。
不管是人生还是做题，必先经历最不利的情况，才能触底反弹，逆风飞翔，方可拥有“无往而不利”的模样。所以，小伙伴们，为了那副“骄傲的模样”，赶紧刷题再走一趟。
