行测数量关系：工程问题

工程问题概述

（一）核心公式

工作总量=工作效率×工作时间

注：

①当工作效率一定的情况下，工作总量与工作时间呈正比例；

②当工作时间一定的情况下，工作总量与工作效率呈正比例；

③当工作总量一定的情况下，工作时间与工作效率呈反比例。

（二）高频考法题干特征

1.给定时间型：题目中只给定不同主体的完工时间，其余量未知。

2.效率制约型：题目中不仅给定工作时间，还给出效率的比例倍数关系。

（三）解题思路：赋值法

1.给完工时间

①赋总量（完工时间的公倍数）

②算效率：效率=总量÷时间

③根据工作过程列方程

完工时间：一次性完成全部工作所需的时间

2.给效率比例

①赋效率（满足比例即可）

②算总量：效率×时间=总量

③根据工作过程列方程

3.条件综合型

这一类区别于前两个题型，题目中关于工程问题公式的三个量给了两个或两个以上的时候，条件较多的工程问题，那么就利用工作总量不变列方程解答即可。

例题1：为支持“一带一路”建设，某公司派出甲、乙两队工程人员出国参与一个高铁建设项目。如果由甲队单独施工，200天可完成该项目；如果由乙队单独施工，则需要300天。甲、乙两队共同施工60天后，甲队被临时调离，由乙队单独完成剩余任务，则完成该项目共需（   ）天。

A.120       B.150       C.180        D.210

【答案】D【解析】第一步，本题考查工程问题，属于时间类。

第二步，赋值工作总量为时间（200天、300天）的公倍数600，则甲的效率是600÷200=3，乙的效率是600÷300=2。

第三步，甲、乙两队共同施工60天后，还剩余工作量为600-（2+3）×60=300。则乙队单独完成需要300÷2=150（天），完成该项目共需60+150=210（天）。

故正确答案为D。

例题2：A、B、C三个工程队负责甲、乙两段工程相同性质的施工，现在先安排3个队伍进行5天甲段工程施工后，调A队伍去做乙段工程，8天后恰好同时完成，已知3个工程队效率之比为5：3：4，如果先安排3个队伍先做甲段，中间调C队去做乙段，也能同时完成，则C队是在工程开始后第（   ）天开始乙段工程。

A.2       B.3        C.4        D.5

【答案】C【解析】第一步，赋ABC三个队的效率分别为5.3.4。

第二步，求总量，甲乙两段工程性质相同，根据“先安排3个队伍进行5天甲段工程施工后，调A队伍去做乙段工程，8天后恰好同时完成”可以算出甲工作总量为（5+3+4）×5+（3+4）×8=116，乙的工作总量为5×8=40。

第三步分析求解，调C队去做乙，共需要40÷4=10天，即C队被调走后10天完成甲工程，则之前做了116-（5+3）×10=36，这36的工作量是三个人一起做的，共36÷（5+3+4）=3天，故第四天开始乙段工程。

故正确答案为C。

例题3：某工程队计划每天修路560米，恰好可按期完成任务。如每天比计划多修80米，则可以提前2天完成，且最后1天只需修320米。问如果要提前6天完成，每天要比计划多修多少米？（   ）

A.160         B.240          C.320        D.400

【答案】B【解析】第一步，本题考查工程问题。

第二步，设原计划修路时间为t天，可列方程：560t=（560+80）×（t-3）+320，解得t=20，可得修路总长度为560×20=11200（米）。

第三步，要想时间提前6天完成，即20-6=14（天）完成，则每天共需修路11200÷14=800（米），那么比原计划每天多修800-560=240（米）。故正确答案为B。

行测工程问题解题技巧：交替合作“3+1”

对于工程问题而言，在实际考试过程中除多者合作外，还会考查交替合作题型。今天和大家来学习交替合作题型的解题方法。

交替合作含义

一般指多个主体一起合作完成一项工作，合作的过程中主体按照一定规律进行轮流完成工作。例如：甲工作1小时，乙工作1小时，丙工作1小时……如此重复下去。在工作的过程中甲、乙是按照每人1小时的工作方式轮流或者合作完工的，因此称之为是交替合作。

解题思路

1.求出工程总量和各个元素的效率。

2.找到最小循环周期，并且求出一个周期工作效率之和。

3.工作总量/一个循环周期的效率和=周期数……剩余工作量。

4.分配剩余工作总量——求出完工时间。

实战练题

例1：完成某片果园的采摘工作，甲单独完成需要18天，乙单独完成需要24天，现按照甲、乙、甲、乙、……的顺序轮流采摘，每人1天，那么完成这项工作需要多长时间？（   ）

A.19.5        B.20          C.20.5          D21

例2：某项工程，甲、乙、丙三个工程队如单独施工，分别需要12小时、10小时和8小时完成。现按“甲—乙—丙—甲……”的顺序让三个工程队轮班，每队施工1小时后换班，问该工程完成时，甲工程队的施工时间共计：（   ）

A.2小时54分     B.3小时       C.3小时54分        D.4小时

总结：工程问题作为行测常考题目类型之一，特点相对明显，题目难度较小，大家只要熟悉各种题目的特点，明确题目的考点，牢记可设特值求解的情况以及解题的步骤，就能在考试的时候如鱼得水。

行测作答技巧：工程问题和行程问题中的正反比

在行测数量关系的学习备考过程中，很多考生都直呼有难度、没思路，持有一种放弃的心态。其实不然，比如今天要带大家学习除了用最基本的方程法解答工程和行程类问题，我们还可以用快、准、狠的正反比解法。其题型明确，解法清晰，可适当减轻大家做这类题目的负担。

一、知识精讲

在一个M=A×B的关系式当中，如果存在一个定值，则另外两个概念有正反比关系存在。

1.当M一定，A与B成反比；

2.当A一定，M与B成正比；

3.当B一定，M与A成正比。

二、工程问题中的正反比

由工作总量=效率×时间可知，当工作总量一定，效率与时间成反比；当效率一定，工作总量与时间成正比；当时间一定，工作总量与效率成正比。

例题：甲工程队计划150天完成A这项工程，按照这样的效率工作30天后，由于新工友的加入，效率提高了20%，则该项工程可以提前多少天完成？（   ）

A.20        B.25        C.30        D.45

【答案】A【解析】新工友加入后，效率提高20%，原效率与现效率之比为1：1.2=5：6，由于剩余的工作总量一定，那么时间与效率成反比，原时间与现时间之比为6：5，那么原时间6份对应150-30=120天，即1份=20天，而现在比原来少用1份时间，那么该项工程可提前20天完工，故此题选A。

三、行程问题中的正反比

由路程=速度×时间可知，当路程一定，速度与时间成反比；当速度一定，路程与时间成正比；当时间一定，路程与速度成正比。

例题：邮递员骑自行车从邮局到渔村送邮件，平时需要1个小时。某天，在距离渔村2公里处，自行车出现故障，改成步行。已知步行速度为自行车车速的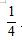，结果比平时多用22.5分钟。问邮局到渔村的距离是多少公里？（   ）

A.15         B.16       C.18         D.20

【答案】B【解析】由题意可知，步行速度与自行车速度之比为1：4，故障地与渔村的距离一定，为2公里，那么速度与时间成反比，即步行时间与自行车时间之比为4：1，所以步行时间比自行车时间多用三份，其对应22.5分钟，即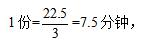即自行车骑行两公里的时间为7.5分钟，所以骑行1小时（60分钟）的距离为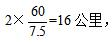即邮局到渔村的距离为16公里，故此题选B。

通过以上题目的总结发现，解决工程和行程类问题，我们只需要找到三个量中的不变量，再根据另外两个量中的已知量之间的比值，推知另一个量的比值关系，找到实际值与比例的对应关系，进而根据题干要求寻找到答案。

吃透这一点，行测工程问题不再难

工程问题研究的是在实际生活生产中，工作总量、工作效率和工作时间三者之间关系的一类问题，属于行测数量关系考试当中的高频考点。认为，工程问题的解题关键是梳理清楚题干描述的完工方式，再结合基本公式（工作总量=工作效率×工作时间）建立等量关系，工程问题就迎刃而解。

示例

生产一批零件，甲车间每天生产100个，乙车间每天生产50个。若两车间合作，8天可以完成。

（1）若甲车间先生产3天后，乙车间加入生产，则共用多少天完成？

（2）若两车间合作，但期间甲休息了3天，乙休息若干天，最终共用12天完成任务。已知每天都有车间进行生产，则乙车间休息了多少天？

【解析】

（1）根据“若两车间合作，8天可以完成”可得工作总量为：（100+50）×8=1200个。

梳理另一种完工方式：根据“甲车间先生产3天后，乙车间加入生产”可知第一阶段是甲独自工作，工作时间为3天；第二阶段甲和乙合作，设工作时间t天；根据实际完成的工作总量为1200个，可列方程：100×3+（100+50）×t=1200，解得t=6，所以共用：3+6=9（天）。

（2）本题的工作总量还是1200个，而另一种完工方式如果按阶段梳理，明显是不可行的，题干并没有明确告诉我们每个阶段是如何工作的，我们可以利用分主体的思维去梳理。根据“两车间合作，但期间甲休息了3天，乙休息若干天，最终共用12天完成任务”可知主体甲休息3天，工作12-3=9天；设主体乙休息t天，则乙工作（12-t）天。根据实际完成工作总量为1200个，可列方程：100×9+50×（12-t）=1200，解得t=6天。

综上，我们不难发现解决这类工程问题的密钥就是梳理完工方式，而近年来经常考察的两种完工方式就是分阶段完工和分主体完工，吃透这一点，工程问题不再难。

例1：甲乙两队完成一项工程的效率比为2∶5。该项工程，若由甲队先单独做3天，再由乙队单独做4天，最后由甲、乙两队合作6天刚好完成。问若由甲队单独完成，需要多少天？（   ）

A.32       B.33       C.34         D.35

【答案】C【解析】设甲乙两队的效率分别为2x和5x，设若由甲队单独完成，需要t天，根据题干可知完工方式：第一阶段甲独自工作3天，第二阶段乙独自工作4天，第三阶段甲和乙合作工作6天，进而可得：2x×3+5x×4+（2x+5x）×6=2xt，解得t=34。

例2：A工程队的效率是B工程队的2倍，某工程交给两队共同完成需要6天。如果两队的工作效率均提高一倍，且B队中途休息了1天，问要保证工程按原来的时间完成，A队中途最多可以休息几天？（   ）

A.4       B.3      C.2         D.1

【答案】A【解析】设B队的效率为x，则A队的效率为2x，根据“工程交给两队共同完成需要6天”可知工作总量为（2x+x）×6=18x。根据“如果两队的工作效率均提高一倍，且B队中途休息了1天，问要保证工程按原来的时间完成”可知另一种完工方式：主体A队休息t天，工作（6-t）；主体B队休息1天，工作5天。虽然两种完工方式不同，但完成的工作总量相等，可得：4x×（6-t）+2x×5=18x，解得：t=4。

随着近几年行测题目灵活性的增强，工程问题的题干也变得比较难理解，但只要梳理清楚完工方式，这类题型将不再困扰你。建议各位考生多找一些工程问题练习总结，以熟练掌握。