
行测指导:巧解概率问题
古典型概率问题
在近几年行测考试中,概率问题逐渐成为命题人青睐的考点。而古典型概率又是概率问题中最常考查的题型,今天就带大家一起来学习这类题目的解法。
一、公式回顾
将事件A发生的概率记为P(A),则:
二、例题精讲
例题:某办公室5人中有2人精通德语。如从中任意选出3人,其中恰有1人精通德语的概率是多少?( )
A.0.5 B.0.6 C.0.7 D.0.75
【解析】从5个人中选出3个人来,总的方法数为 种,而当中恰有一人精通德语,则应该在精通德语的两人中选出1人来,即
种,而当中恰有一人精通德语,则应该在精通德语的两人中选出1人来,即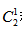 种,而要选出3人,那么还差着两人,只能从不会德语的3个人中选出2人,则为
种,而要选出3人,那么还差着两人,只能从不会德语的3个人中选出2人,则为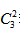 种,所以概率应该为
种,所以概率应该为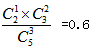 。
。
例题:某人的银行卡密码是6位数字,一天内连续输错三次密码,银行卡将会被锁定,则此人在一天内成功解锁的概率是多少?( )
【解析】密码可输入的数字在0-9之间,共10个数字,密码由6位数组成,因此密码的所有组成情况有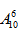 ,即151200种。此人要在一天内成功解锁有三种情况,分别是第一次成功、第二次成功或第三次成功。第一次输入的数是在151200种中任选一种,因此成功的概率为
,即151200种。此人要在一天内成功解锁有三种情况,分别是第一次成功、第二次成功或第三次成功。第一次输入的数是在151200种中任选一种,因此成功的概率为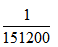 ;若第一次不成功,则第二次不会再输入相同的数,即第二次输入的数的总情况数151200-1=151199种,所以第二次成功的概率
;若第一次不成功,则第二次不会再输入相同的数,即第二次输入的数的总情况数151200-1=151199种,所以第二次成功的概率 ,同理,第三次解锁成功的概率
,同理,第三次解锁成功的概率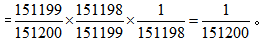
综上,一天内解锁成功的概率=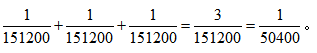
三、总结
以上是行测考试中概率问题(古典型概率)解题方法。需要提醒大家的是,近年来公务员中对概率问题的查考难度加大。要解决好这类问题,考生一定要打好坚实的基础,此外,还要学好排列组合,因为在计数方式的考察里面枚举法相对的考察较少,对于计数较大的情况更好的用排列组合的方式可以更快机算,以不变应万变。
行测数量关系:古典概率该咋做
在行测数量关系中,概率问题属于高频考点,尤其是古典概率,那么对于一个古典概率的题来说,应该怎么入手去做呢?今天就跟大家探讨一下古典概率的做法。
所谓古典概率,就是可以求得出来的概率,其有两个明显的特征:①样本数是有限的;②每个样本等可能发生。基本公式为: 对于这个公式,我们在使用的时候可以从以下步骤走:第一步先从“总的等可能事件的样本数”入手,分析一下题干整体上是想让我们去干一件什么事情,然后再去看“A事件发生的样本数”,即从问题入手,看问题最终要求的是什么,这样下来,基本答案就可以出来了。
对于这个公式,我们在使用的时候可以从以下步骤走:第一步先从“总的等可能事件的样本数”入手,分析一下题干整体上是想让我们去干一件什么事情,然后再去看“A事件发生的样本数”,即从问题入手,看问题最终要求的是什么,这样下来,基本答案就可以出来了。
例1:甲、乙两人相约骑共享单车运动健身。停车点现有9辆单车,分属3个品牌,各有2辆、3辆、4辆。假如两人选择每一辆单车的概率相同,问两人选到同一品牌单车的概率约为:( )
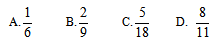
【答案】C【解析】问题最后求概率,所以我们可以按照步骤先去看“总的等可能事件的样本数”,这道题是一共有9辆车,两个人每个人选择一辆车也就是从9辆车里面选择2辆,则总样本数为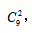 接下来去看“A事件发生的样本数”即从问题入手,问题要求两个人选到同一品牌的单车,分析一下可得:两人选到同一品牌可以选有2辆车的品牌,即
接下来去看“A事件发生的样本数”即从问题入手,问题要求两个人选到同一品牌的单车,分析一下可得:两人选到同一品牌可以选有2辆车的品牌,即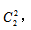 还可以选3辆车的品牌,即
还可以选3辆车的品牌,即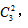 也可以选4辆车的品牌,即
也可以选4辆车的品牌,即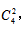 最终所求概率为
最终所求概率为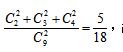 故答案选择C。
故答案选择C。
例2:某人想要通过掷骰子的方法做一个决定:他同时掷3颗完全相同且均匀的骰子,如果向上的点数之和为4,他就做此决定。那么,他能做这个决定的概率是:( )
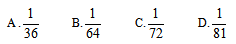
【答案】C【解析】题干最后求概率相关,根据公式,先从步骤一开始,梳理题干可知本题要掷3颗骰子,样本总数为6×6×6=216,第二步分析问题可知需要三个点数之和为4,可能情况为(1,1,2)、(1,2,1)、(2,1,1),样本数为3,故所求概率为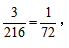 故选择C。
故选择C。
希望通过以上两个题目的分析,大家可以对概率的解题思路及步骤有了深入的认识,在后面的备考中多练习,熟能生巧之后再也不怕概率相关的题。
行测概率问题还在丢分?一招教你快速解题!
一提到行测的数量关系,很多考生都望而却步,尤其是数量关系里的概率问题更是让考生头大。但其实只要用对了方法,概率问题也能又快又准的选出答案。今天就教大家一招,用定位法快速解决概率问题,让你的弱项变成强项。
一、基本公式:
 (定位法求解的概率问题其实是古典概率中的一种,故而公式跟古典概率的公式是一样的)
(定位法求解的概率问题其实是古典概率中的一种,故而公式跟古典概率的公式是一样的)
二、题型特征:当遇到要同时考虑相互联系的元素时(例如:同一排,同一列,同一组,同一辆车……)。
三、解题技巧:可以先将其中一个固定,再考虑其他元素的所有可能样本,从而进行求解。
例1:一张纸上画了5排每排6个共30个格子,现将1个红色和1个绿色旗子随机放入任意一个格子(两个棋子不在同一个格子),则2个棋子在同一排的概率是多少?( )
A.不高于15% B.高于15%低于20% C.正好为20% D.高于20%
【答案】B【解析】通过问题“2个棋子在同一排的概率是多少”判断得知,可用定位法来解题。先将红棋子固定,那么此时对于绿棋子来说还有29个位置可以放,其中跟红棋子一排的还有6-1=5个位置,故两人在同一排的概率为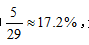 选择B选项。
选择B选项。
例2:从A市到B市总共有15趟大巴车,共300个位置,每辆车座位数相同,小张跟小李在同一天都要从A市到B市,买票前没有任何沟通,问小张跟小李坐在同一辆大巴的概率有多大?( )
A.不高于10% B.高于10%低于15% C.正好为15% D.高于15%
【答案】A【解析】通过问题“小张跟小李坐在同一辆大巴的概率有多大”判断可知,可用定位法来解题。因为每辆车座位数相同,故而每辆车都有300÷15=20有个座位。现将小张固定,那么此时对于小李来说还有299个座位可以坐,其中跟小张同一辆车的还有19个位置,故两人在同一辆车的概率为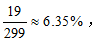 选择A选项。
选择A选项。
总结:考生做题时在辨明题型后,在固定一个的基础上可以先找到总的等可能样本数,再找到满足问题中具有限制条件的等可能样本数,进而解题。
“业精于勤荒于嬉,行成于思毁于随”,各位考生平时也要多加练习,将这些知识点内化,不断提高正确率!
行测数量关系概率问题新思路——定位法
行测数量关系近些年会考查到一种重要题型——古典概率,而多数考生对概率问题可以说是避而远之,毕竟在考试中按照常规方法做会耽误较长时间。但是古典概率里有一些题目是可以快速解题的,接下来就给大家展示这些题目的特别之处吧!
例1:某单位的会议室有5排共40个座位,每排座位数相同。小张和小李随即入座,则他们坐在同一排的概率( )
A.不高于15% B.高于15%但低于20%
C.正好为20% D.高于20%
【答案】B【解析】小张和小李随机入座的总样本数为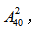 每排40÷5=8个座位,他们两人坐在同一排的样本数为
每排40÷5=8个座位,他们两人坐在同一排的样本数为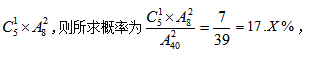 选择B。
选择B。
此题可以通过求总事件和A事件发生的等可能样本数解出来,但是大多数同学对于排列组合的知识掌握得不是很好,对这道题就比较头疼。现在给大家提供一种更快的解题新思路。
【解析】先将小张的座位固定,剩39个座位小李可以选,小李要和小张坐在同一排,只能在小张坐的那一排剩余的7个位置上选,故两人坐在同一排的概率是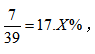 选择B。
选择B。
【方法总结】通过两种方法的对比,第二种更得人心,这种方法叫做定位法。定位法求古典概率的题型特征:问法中出现“同一排、同一队、(不)相邻”等的要求,即两个元素之间相互联系,可以先将其中一个固定,再考虑其他元素的所有可能情况,从而进行求解。
现在练习巩固一下定位法求古典概率吧!
例2:A、B两地间有三种类型列车运行,其中高速铁路动车组列车每天6车次,普通动车组列车每天5车次,快速旅客列车每天4车次。甲、乙两人要同一天从A地出发前往B地,假设他们买票前没有互通信息,而且火车票票源充足,问:他们买到同一趟列车车票的概率有多大?( )
A.小于10% B.10%到20%之间
C.20%到25%之间 D.25%到30%之间
【答案】A【解析】车次共6+5+4=15种。先将甲选择的车次固定,乙可以选择的车次有15种,他们要想买到同一趟列车,乙只能选择甲买的那一趟,即1种选择。故他们买到同一趟列车的概率为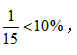 选择A。
选择A。
通过上述题目,相信大家对于定位法求古典概率问题也不再那么抵触了,只要勤加练习,就能快速解出答案。各位同学赶紧找一些题目练手,体验一下解决它们的乐趣吧!








