政华公考

【答案】B【解析】抽调情况为抽调两个科室且每个科室各抽调1人，假设这三个科室分别是A、B和C，首先根据抽调科室可分为三类：①A和B；②A和C；③B和C，其次计算每一类的方法数，①A和B：从A科室抽调1人，有7种选择，从B科室抽调1人，有9种选择，从A抽调、从B抽调两者缺一不可，故属于分步思维，方法数为7×9=63种；同理计算②A和C：7×6=42；③B和C：9×6=54。最后将三类方法数相加，则有63+42+54=159，正确答案为B。

例2：某企业国庆放假期间，甲、乙和丙三人被安排在10月1号到6号值班。要求每天安排且仅安排1人值班，每人值班2天，且同一人不连续值班2天。问有多少种不同的安排方式（）？

A.15 B.24 C.30 D.36

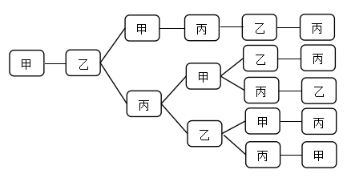
【答案】C【解析】根据题意需要安排甲乙丙三人在10月1号到6号值班，6天中每天安排1人，每人值班2天且不连续。那么第一步可以先安排1号，甲、乙、丙三人选一人值班，有3种选择。第二步安排2号，由于每人值班不连续，所以从剩下两人中选一人，有2种选择。第三步安排3-6号，安排3号值班的人可以和1号值班的人相同，也可以和1号、2号值班人员均不同，而3号值班的人是否和1号值班人员相同，会影响后面日期的安排，所以需分类讨论。假设1号安排甲，2号安排乙(如下图所示)，则3号安排分两类：①安排甲；②安排丙。计算每一类方法数：①安排甲：根据题干条件，4号只能安排丙，5号安排乙，6号安排丙，有1种情况。②安排丙：4号可以安排甲或者乙，若4号安排甲，5号可以安排乙或者丙，6号即为剩下一人值班，有2种；同理，若4号安排乙，5号可以安排甲或者丙，6号也是剩下一人值班，有2种，则共有2+2=4种，则第三步共有1+4=5种。最终分步相乘3×2×5=30种，正确答案为C。

排列组合四种常用方法讲解

排列组合一直都是比较难把握的知识点，在行测考试中，也是常考的一种题型。很多考生对于排列组合问题怎么做，方法如何用感到非常困惑。那么今天我们就针对排列组合问题中四种常见题型进行简单说明。

一、优限法

遇到某些元素有特殊要求，我们优先解决这类元素的方法。

例1：由数字1、2、3、4、5、6、组成无重复的七位数字，求数字1必须在首位或末尾的七位数的个数（）。

A.120 B.240 C.360 D.480

【答案】B【解析】根据题意可知数字1相对于其他五个数字是存在特殊要求，因此我们在解题时候应该优先处理这个对象。由于数字1只能在首位或末尾，因此我们可以从两个位子当中任意挑出一个位置放数字1，共有：数字1放完之后，其余五个数字可以任意排放，因此共有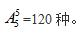：因此总共有：2×120=240种。

二、捆绑法

用来解决遇到某几个元素必须站在一起或者必须排在一起情况，解题时候我们可以将必须一起的元素捆绑在一起，然后再解决其他没有限制条件的元素。

例2：六个人一起排成一排进行拍照留念，其中甲乙必须站在一起，问按照这种拍照方式，总共有多少种拍照方法（）？

A.120 B.240 C.360 D.480

【答案】B【解析】甲乙两个人必须站在一起，所以我们在解题的时候可以先将甲乙两人当做是一个整体捆绑在一起，但是对于他们两个内部，是有顺序之分，因此有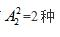方法，除了甲乙之外，还剩下四个人，加上捆在一起的甲乙一人，这时候他们任意排剩下5个位置，因此有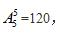因此总共有：2×120=240种。

三、插空法

用来解决某几个元素必须不在一起或不相邻的情况，解题时候，我们可以先将没有限制条件的其余元素先进行排序，然后再将不相邻的元素插入他们的间隙或者两端位置。

例3：六个人一起排成一排进行拍照留念，其中甲乙必须不站在一起，问按照这种拍照方式，总共有多少种拍照方法（）？

A.120 B.240 C.360 D.480

【答案】D【解析】除了甲乙两个人外，总共还有另外四个人，那么四个人先进行排序总共有：四个人排完之后，总共产生了五个位置，然后我们将甲乙两人插入的五个间隙中任意的两个间隙，因此有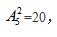：因此总共有：24×20=480种方法。

四、间接法

当遇到正面思考比较复杂时候，往往它的对立面可能只有一种或者两种情况，因此我们可以利用对立面情况来间接求解。

例4：甲、乙、丙、丁、戊、己6人站成一排进行排队，其中甲、乙、丙要求至少有一个人在左三位置，共有多少种排法（）？

A.456 B.324 C.360 D.684

【答案】D【解析】甲、乙、丙三个人至少有一个人站在前三个位置，那么总的情况可能存在一个人或者两人或者三人都在前三个位置的情况。但是跟这个条件相对立的情况却只有一种：三个人都不在前三个位置，那么三个人都不在前三个位置的情况有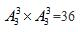：种。总的情况有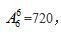：因此甲、乙、丙至少有一个人在前三个位置的情况有：720-36=684种。

最后，提醒各位同学们在牢记排列组合基本原理的前提下，注意利用常用方法进行解题，相信，只要大家勤加演练，定能征服排列组合问题！

行测环形排列组合题的正确打开方式

在行测考试中，对于排列组合题目的考查热度不减，题型也是变幻莫测，今天就来跟大家一起探讨排列组合问题中的一种类型——环形排列组合，这种题目解法思路相对来说比较固定，只需要用特定的公式来进行求解即可，下面带大家一起来看看。

一、什么是环形排列组合

如果“n个人围成一个圆圈，问有多少种不同的方法？”在所有人相对位置不变的情况下，整体顺时针或者逆时针换位置的时候，只是我们观看的角度发生了变化，其实坐的方法和原来是一样的。所以此类题型的解题方法就是：先固定住一个人，让其他人进行全排列即可，即有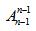方法。

二、计算公式

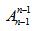
三、例题展示

例1：现有A、B、C、D、E五个老朋友中秋聚会，五人围桌而坐，问共有多少种不同的坐法（）？

A.24 B.36 C.72 D.120

【答案】A【解析】五个人围坐成一个圈，不管是逆时针还是顺时针摆放，它们的相对位置并没有改变，故按照环形排列组合公式可得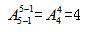：×3×2×1=24种，故本题选择A。

例2：5个小朋友围成一圈做游戏，小芳和小明需要挨在一起，问有多少种安排方法（）？

A.6 B.12 C.24 D.48

【答案】B【解析】5个小朋友围成一圈，且小芳和小明要挨在一起，首先考虑把小芳和小明进行捆绑看成一个元素，即现在变成4个元素环形排列，直接应用环形排列组合公式，总的情况数应为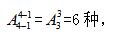：但是小芳和小明内部有顺序要求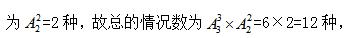，故本题选择B。

以上便是关于环形排列组合的一些常见题型以及求解思路，值得注意的是，环形排列组合的考查形式多样，但是无论如何变化，首先要确定的是几个对象的环形排列，然后再根据公式求解即可。

一招搞定行测隔板模型

在行测考试中，排列组合一直是高频考点，同时也是让很多考生头疼的考点，但是对于排列组合一些特定的模型，只要掌握正确方法还是能够快速拿分，其中隔板模型就是其中一种，看似很难，到那时只要掌握住隔板模型的主要题型特征和解题技巧，这种题就不在话下。

隔板模型

定义：将n个相同的元素分给m个不同的对象，每个对象至少一个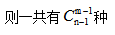，方法。

题型特征：①元素相同；②每个对象至少分一个；③元素要分尽

示例：7个相同的桔子分给4个幼儿园小朋友，每个小朋友至少分一个，共有多少种分配方法？

如图所示，假设〇表示7个相同的桔子，要想把桔子分成四份，分给四个不同的小朋友，可考虑用隔板将其分成4份，每份至少一个，按顺序分给四个人即可；7个桔子中间产生6个空隙可放隔板，故从6个空隙中选出3个空隙放入隔板即可分成四份。故分配方法为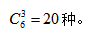

结论应用

例1：某部门申请到12个优秀员工名额，分配给其5个部门，每个部分至少分配一个名额，则有多少种分配方法（）？

A.210 B.280 C.330 D.375

【答案】C【解析】结合题意，即将12个相同元素分给5个不同的对象，每个对象至少一个，符合隔板模型的基本特征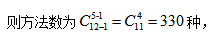，故选择C选项。

例2：某城市一条道路上有4个十字路口，每个十字路口至少有2名交通协管员，现将10个协管员名额分配到这4个路口，则4个路口协管员名额的分配方案有：（）

A.10种 B.15种 C.20种 D.35种

【答案】A【解析】10个协管员名额分配到这4个路口，每个十字路口至少有2名交通协管员，不满足每个对象至少一个的特征，对其变形，可每个十字路口先分配1个名额，再把剩下6个名额分配给4个十字路口，每个路口至少分配1名即可，则方法数为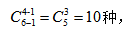故选择A选项。

排列组合问题是大家在学习阶段相对棘手的知识点，但是在行测考试中，难度往往都是中等，甚至对一些于特殊模型，反而更容易掌握拿分，而隔板模型就是其中一种，通过以上讲解相信大家一定会有更深的认识和理解，关注，为你备考路上排忧解难！