行测数量关系之不定方程解题方法
行测数量关系不定方程的三大解题思路
行测数量关系部分经常考查不定方程这类题型，所谓不定方程，是指未知数的个数多于方程个数，且未知数受到某些限制（如有理数、整数、正整数等）的方程或方程组。解不定方程一定要讲究方法和技巧，在此为大家梳理一下解不定方程的巧妙所在。
一、利用整除特性求解
当等式右边的常数和某个未知数系数能被同一个数整除（1除外）时，即能说明含另外一个未知数的代数式也能被这个整数整除。
例1：超市将99个苹果装进两种包装盒，大包装盒每个装12个苹果，小包装盒每个装5个苹果，共用了十多个盒子刚好装完。问两种包装盒相差多少个？（ ）
A.3 B.4 C.7 D.13
【答案】D【解析】按照题目当中等量关系，可得方程12x+5y=99，由于x、y是整数，所以99能被3整除，12x也能被3整除，由此可得5y也能被3整除，从而判定y能被3整除，y=3，x=7（舍去），y=15，x=2，符合题意，差为13，因此选择D。
二、利用尾数特性求解
尾数即一个数的末尾数字。当出现某个未知数的系数是5或10时，应该想到用尾数法求解。因为5的倍数的尾数只有0或5这两种可能，而10的倍数的尾数只有0，分情况去分析时比较简单。
例2：超市将99个苹果装进两种包装盒，大包装盒每个装12个苹果，小包装盒每个装5个苹果，共用了十多个盒子刚好装完。问两种包装盒相差多少个？（ ）
A.3 B.4 C.7 D.13
【答案】D【解析】按照题目当中等量关系，可得方程12x+5y=99，由于x、y是整数，所以等式后侧尾数为9，5y的尾数要么0，要么5，只有5符合，12x的尾数为4。12x的尾数为4，要么24，要么84，只有24符合。因此求出x=2，y=15，差为13，因此D。
三、利用奇偶性求解
基础特性：
奇数+奇数=偶数；偶数+偶数=偶数；奇数+偶数=奇数；
奇数-奇数=偶数；偶数-偶数=偶数；奇数-偶数=奇数；
奇数×奇数=奇数；偶数×偶数=偶数；奇数×偶数=偶数。
例3：超市将99个苹果装进两种包装盒，大包装盒每个装12个苹果，小包装盒每个装5个苹果，共用了十多个盒子刚好装完。问两种包装盒相差多少个？（ ）
A.3 B.4 C.7 D.13
【答案】D【解析】按照题目当中等量关系，可得方程12x+5y=99，由于x、y是整数，12x是偶数，99是奇数，所以得出5y是奇数，得出y为奇数，只有y=15，x=2符合，因此差为13，选择D项。
上述是不定方程的三种解法，根据这些方法结合选项，能快速求解不定方程。在实际练习题目时，建议各位考生优先利用整除思想，出现5的倍数时可以优先考虑尾数法，出现2的倍数时优先考虑奇偶性解不定方程。
行测数量关系：巧解不定方程的三个好办法
方程法是解决行测数量关系题目的重要方法之一，对大多数考生而言，解普通方程难度不大，但是求解不定方程，除了最基本的代入排除之外，还能如何更快、更准确地解出正确答案呢？带大家来了解一下：
一、不定方程的定义
当未知数的个数大于独立方程的个数时，我们称这样的方程为不定方程。在实数范围内，不定方程的解会有无数组，是不固定的。
二、正整数范围内求解不定方程
解不定方程时根据未知数的取值特点进行讨论，会大大减少讨论的次数，所以根据不定方程的特点，常用的解不定方程的方法除代入排除外，还可结合整除、奇偶性和尾数法等多种方法求解。
1.看到系数和常数有公约数，优先想整除
例1：小张的孩子出生的月份乘以29，出生的日期乘以24，所得的两个乘积加起来刚好等于900，问孩子出生在哪一个季度？（ ）
A.第一季度 B.第二季度 C.第三季度 D.第四季度
【答案】D【解析】设出生月份为x，出生日期为y，月份和日期都是正整数，则29x+24y=900，问题为出生的哪一季度，需要知道小张孩子出生的月份，即x的值。由于24、900有公约数12，即都是12的倍数，所以29x也应是12的倍数，且29并不是12的倍数，则x应是12的倍数，即出生月份为12月，也就是第四季度。选择D选项。
方法总结：在不定方程中，当其中一项未知数的系数与常数项有除1外的公约数时，可结合整除特性分析排除错误选项。
2.系数有奇有偶，方程不用愁
例2：某单位向希望工程捐款。其中部门领导每人捐50元，普通员工每人捐20元，部门所有人共捐款320元，已知该部门总人数超过10人，问该部门可能有几名部门领导？（ ）
A.1 B.2 C.3 D.4
【答案】B【解析】设领导有x人，普通员工y人，人数必须为正整数，则50x+20y=320，化简得5x+2y=32。32和2y是偶数，则5x必然是偶数，x为偶数，排除A、C。若领导有4人，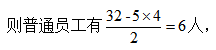
总人数没有超过10，若领导有2人，
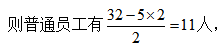总人数超过10人，故领导为2人，答案选B。
方法总结：在不定方程中，当未知数的系数为一奇一偶时，可结合奇偶性分析，排除错误选项。
3.系数是5的倍数，尾数来帮你
例3：现有451个同样大小的橙子装入大、小两种袋子中，已知大袋每袋装20个橙子，小袋每袋装17个橙子，每个袋子都必须装满，问至少需要小袋子的个数：（ ）
A.5 B.3 C.13 D.9
【答案】B【解析】设大袋子有x个，小袋子有y个，根据题意小袋子、大袋子共装了451个橙子，可列方程20x+17y=451。由于x、y均为整数，20x的尾数一定为0，则17y的尾数必为1，排除A、D，代入B符合题意。
方法总结：当不定方程的解有正整数范围限制时，若未知数的系数是5的倍数，那么该项的尾数就是0或5，就可以结合常数项的尾数将另外一项的尾数确定，进而排除错误选项。
以上三种方法并不是孤立存在的，根据不同方程特点，考生们可以灵活选择，甚至三种方法可以结合到一起使用。
行测不定方程组考查的两种题型
近年来，行测题目考查越发地灵活。如数量关系中求解不定方程的基本题型外，还会考查一些变形问题，主要有两类，同学们在做题的时候就比较容易混淆，实际上只要掌握了题目具体提问方式，就会变得很简单。下面，就带大家一起来看一下不定方程组的两种考查题型。
例1：如果买4支相同的铅笔和8个相同的笔记本需要25元，买8支相同的铅笔和16支相同的钢笔需要46元，若要买5支相同的铅笔、5支相同的钢笔和5个相同的笔记本，则需要多少元？（ ）
A.30 B.35 C.40 D.45
【答案】A【解析】方法一，设一支铅笔x元，一个笔记本y元，一支钢笔z元，则根据题意可得4x+8y=25①，8x+16z=46②，①×2+②可得8x+16y+8x+16z=96，则x+y+z=6，故所求为5（x+y+z）=30。
方法二，设一支铅笔x元，一个笔记本y元，一支钢笔z元，则根据题意可得4x+8y=25①，8x+16z=46②，因为方程个数小于未知数个数，所以方程有无穷多组解，可涉其中一个未知数为特值，可令x=0，则与此对应的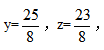
所以5（x+y+z）=30。
例2：某种考试已举行了24次，共出了试题426道，每次出的题数或者为25题，或者为16题，或者为20题，那么考25题的有多少次？（ ）
A.4 B.2 C.6 D.9
【答案】B【解析】设考25道、20道、16道的次数分别是x、y、z次。由题x+y+z=24①，25x+20y+16z=426②，②-①×16，可得9x+4y=42。
方法一，9x和42均能被3整除，则4y能被3整除，即y能被3整除，当y=3时，x非整数，不满足题意；当y=6时，x=2，满足题意，故考25题的有2次。
方法二，42、4y均是偶数，所以9x是偶数，9不是偶数，所以x是偶数，排除D；代人A，当x=4时，y=1.5，不是整数，不满足题意；代人B，当x=2时，y=6，满足题意，直接选B。
区分：分析这两类题型，第一个题目，是求解的是x，y，z的组合值，而我们第二题是求解的某个未知数的值。
解题方法：遇到第一组求x，y，z的组合值，可以利用设某个未知数特值为零的方式去进行求解；遇到第二组不定方程组求解其中未知数的数值，我们可以采用“降维”的思想求解，即将方程的个数降为一个，未知数降为两个，进行求解。
通过以上题目，我们可以看到解决不定方程组的题型，希望同学们能通过这次学习，把这两种题型区分清楚，大家可以多找一些此类题目练习，以便熟练地掌握此种方法。
不定方程的解题思路
不定方程（组）是指未知数个数多于方程个数，不能通过一般的消元法直接得到唯一解，常与差倍比问题、利润问题等热门考点相结合，故需要考生们在备考的过程中加以重视。今天与大家一起探讨一下考试中不定方程（组）的解题思路。
不定方程（组）包含不定方程与不定方程组，而根据题目条件对未知数是否必须为整数的限制，可以将不定方程组分为限定性不定方程组和非限定性不定方程组。前者指未知数必须为正整数，后者则无此要求。两种类型的不定方程组问题都有其固定的解题思路，方法性与技巧性比较强，掌握相应的思路去解题便会事半功倍。
不定方程
题型特征：根据题干可列出一个包含两个未知数的方程。
解题方法：首先分析奇偶、倍数、尾数等数字特性，然后尝试代入排除。
例【2015联考】每年三月某单位都要组织员工去A、B两地参加植树活动，已知去A地每人往返车费20元，人均植树5棵，去B地每人往返车费30元，人均植树3棵，设到A地有员工x人，A、B两地共植树y棵，y与x之间满足y=8x-15，若往返车费总和不超过3000元时，那么，最多可植树多少棵（ ）？
A.498 B.400 C.489 D.500
【解题思路】已知植树棵数y=8x-15，一个方程两个未知数为不定方程，8x为偶数，15为奇数，偶数-奇数=奇数，则y为奇数，排除A、B、D项，正确答案为C。
【点评】本题若采用常规解方程的方法也可解题，但耗费时间久，不适合考场使用。本题不需要算车费等其他数值，因此可利用数字特性直接锁定答案。
不定方程组
1.限定性不定方程组
题型特征：可根据题意列出方程组，未知数多于方程数，且未知数必须为正整数，常用来表示人数、盒子或者其他物体的个数等。
解题方法：先消元转化为不定方程，再按不定方程求解。
例1【2017江苏】小王打靶共用了10发子弹，全部命中，都在10环、8环和5环上，总成绩为75环，则命中10环的子弹数是：（ ）
A.1发 B.2发 C.3发 D.4发
【解题思路】设命中10环、8环、5环的子弹数分别为正整数x、y、z。由子弹总数为10发，总环数为75环，可列不定方程组：
x+y+z=10……①；
10x+8y+5z=75……②；
求命中10环子弹数x，由②-①×5可得不定方程5x+3y=25。5x、25均为5倍数，3y也必然为5倍数，y只能为5，此时x=2，正确答案为B。
【点评】将不定方程组消元变为不定方程时，求谁保留谁，消掉另外两个未知数中较好计算的一个。本题也可直接分析方程②，10x+8y+5z=75中，10x、5z、75均为5的倍数，则8y一定也是5的倍数，y=5、10、15…，加和不能超过75，则y=5，代入求解同样可以锁定B项。但该方法有局限性，如当z的系数为6时无法使用，需要根据具体题目具体分析。
例2【2018四川下】某企业采购A类、B类和C类设备各若干台，21台设备共用48万元。已知A、B、C类设备的单价分别为1.2万元、2万元和2.4万元。问该企业最多可能采购了多少台C类设备？（ ）
A.16 B.17 C.18 D.19
【解题思路】设该企业采购A类、B类和C类设备数量分别为A、B、C。已知“21台设备共用48万元”，则A+B+C=21……①，1.2A+2B+2.4C=48……②。联立两式，②×5-①×6可得：4B+6C=114，化简得：2B+3C=57。由于设备购买数量一定是不为零的整数，根据倍数特性，57和3C均可以被3整除，则2B一定可以被3整除。若要C类设备最多即B最小，B最小为3，代入原式可得：C=17，A=1，符合题意。因此该企业最多可能采购了17台C类设备，正确答案为B。
【点评】消元时也可消掉B，②-①×2可得：-0.8A+0.4C=6，约分得：-2A+C=15，即C-2A=15。2A为偶数，15为奇数，奇数-偶数=奇数，则C必须是奇数，排除A、C项。剩二代一，题干要求“最多”，因此从最大的选项开始代入，代入D项：19-2A=15，解得A=2，B=0，由于设备购买数量一定是不为零的整数，故B≠0，排除D项。提示大家，正确答案有且仅有一个，排除掉三个错误答案后，剩下的一定为正确答案，无需再次验证。
2.非限定性不定方程组
题型特征：可根据题意列出方程组，未知数多于方程数，且未知数不一定为正整数，常指物品的价格、工作的时间等，需要求解的是一组未知数的和。
解题方法：特值法（赋零）或配系数法。
当未知数表示时间和钱，可以为小数，这样的方程组有无数组解，有好多解都满足方程，随便找一组即可，而0最简单，因此可以用赋零法。建议使用时让最复杂的未知数为0，代入进行计算。而配系数法中系数是凑出来的，若考场上无法凑出来，则无法求解，因此建议用赋零法解题。
例1【2016春季联考】木匠加工2张桌子和4张凳子共需要10个小时，加工4张桌子和8张椅子需要22个小时。问如果他加工桌子、凳子和椅子各10张，共需要多少小时？（ ）
A.47.5 B.50 C.52.5 D.55
【解题思路】假设每张桌子、凳子、椅子的所需时间分别为a小时、b小时、c小时，则2a+4b=10、4a+8c=22，化简得到a+2b=5①，a+2c=5.5②，①+②=2a+2b+2c=10.5，则10（a+b+c）=52.5，所需时间52.5小时，正确答案为C。
【点评】本题中未知数为时间，时间不一定是整数，且要求的量为一组数的和，若考生数字敏感性较差，无法通过配系数求解，也可用赋零法解题。赋值a=0，原方程组可转化为4b=10，8c=22，4（b+c）=21，10（a+b+c）=52.5。
例2【2018上海】现有甲、乙、丙三种货物，若购买甲1件、乙3件、丙7件共需200元；若购买甲2件、乙5件、丙11件共需350元。则购买甲、乙、丙各1件共需多少元？（ ）
A.50 B.100 C.150 D.200
【解题思路】根据题干条件，假设甲、乙、丙的价格依次是x、y、z元，则根据题意可列方程组：x+3y+7z=200①，2x+5y+11z=350②。赋丙的价格为0，即z=0。原方程组转化为x+3y=200；2x+5y=350，解得：x=50，y=50。可得：x+y+z=50+50+0=100元，正确答案为B。
【点评】若采用配系数法，可将原方程组：x+3y+7z=200①，2x+5y+11z=350②，①×3得：3x+9y+21z=600③，②×2：4x+10y+22z=700④，④-③解得x+y+z=100。配系数法不是每道题都适用，需要较强的数字敏感度，建议优先掌握赋零法。
掌握不定方程（组）的解法可有效提高和差倍比、经济利润、年龄问题等常考题型的解题速度与正确率，建议各位考生加强练习，熟练运用。
