行测数量关系：教你巧解行程问题
相遇追及
在行测考试中，行程问题是常见的一种考题，其实常见的行程问题相对来说在常考各大题型中算较简单的一类题型。我们需要牢牢地把握行程问题的基本公式：路程=速度×时间。今天为大家讲解行测数量关系行程问题中常考的两种问题：相遇和追及问题。
相遇问题
如图：甲乙二人分别同时从AB两地出发相向而行，在C点相遇，我们可知：
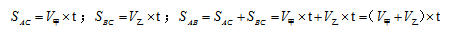
例1：有甲、乙、丙三人，甲每小时走80公里，乙每小时走70公里，丙每小时走60公里。现在甲从A处出发，乙、丙两人从B处同时出发相向而行，在途中甲与乙相遇15分钟后，甲又与丙相遇。求AB两地的距离（ ）。
A.315公里 B.525公里 C.465公里 D.455公里
【答案】B【解析】在这个题目中，三个人的速度都有，相遇距离就是两地之间的整个全程，不管是甲丙之间还是甲乙之间，都是同一个全程。那我们就可以围绕路程建立等量关系：设甲乙相遇的时间为T，那么甲丙相遇时间为T+1/4，利用相遇公式有(80+70)T=(80+60)(T+1/4)，解得T=3.5，因此整个距离为(80+70)×3.5=15×35=525，所以答案选B。
追及问题
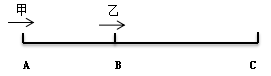
如图：甲乙二人分别同时从A、B出发前往C地，最终甲乙两人同时到达C地，我们可知：
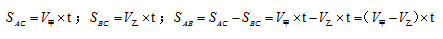
即：路程差=速度差×时间
例2：高速公路上行驶的汽车A的速度是100公里每小时，汽车B的速度是120公里每小时，此刻汽车A在汽车B前方80公里处，汽车A中途加油停车10分钟后继续向前行驶。那么从两车相距80公里处开始，汽车B至少要多长时间可以追上汽车A（ ）？
A.2小时 B.3小时10分 C.3小时50分 D.4小时10分
【答案】B【解析】由题干可知，在追的过程中，A加油10分钟，可以先让A加油10分钟，这样就相当于B车在这10分钟走了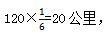
所以两车同时走的那一瞬间的距离为80-20=60公里，根据追及路程=路程差=速度差×时间可得：60=(120-100)×追及时间，解得追及时间为3小时；因为B车先走了10分钟，然后又追了3小时，所以总共用时3小时10分钟，故选B。
相遇追及模型
在行测考试中，数量关系是单题分值比较大的专项，也是提分的关键，其中行程问题是一种常见的题型，需引起每一位考生的重视。行程问题相对而言是种比较复杂的题型，但其中的相遇追及问题比较简单，容易掌握，也是考试常见类型，今天就来带大家学习行程问题中的相遇追及问题。
一、相遇追及模型
1、相遇模型
甲、乙分别从A、B两地同时相向而行，t时间后甲、乙相遇。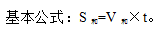
2、追及模型
甲、乙分别从A、B两地同时同向而行，t时间后甲追上乙。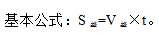
二、常见题型
例1：A、B两架飞机同时从相距1755公里的两个机场起飞相向飞行，经过45分钟后相遇，如果A机的速度是B机的1.25倍，那么两飞机的速度差是每小时（ ）公里。
A.250 B.260 C.270 D.280
【答案】B【解析】A、B同时异地相向而行为典型的相遇模型，设B机的速度为每小时v公里，则A机的速度为每小时1.25v公里，所求为1.25v-v=0.25v，由于45分钟=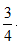
小时，所以通过基本公式可知1755=(1.25v+v)×
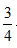，解得0.25v=260，故选择B项。
例2：甲车上午8点从A地出发匀速开往B地，出发30分钟后乙车从A地出发以甲车2倍的速度前往B地，并在距离B地10千米时追上甲车。如乙车9点10分到达B地，问：甲车的速度为多少千米/时（ ）？
A.60 B.45 C.36 D.30
【答案】D【解析】设甲车的速度为v千米/时，则乙车的速度为2v千米/时，设乙从A地出发用t小时在C点追上甲车，作图如下：
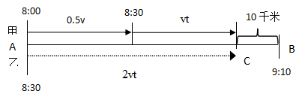
乙出发时，甲、乙同时异地同向而行为典型的追及模型，由基本公式可知：0.5v=(2v-v)×t，解得t=0.5，因此乙车追上甲车时为9点，则乙车用10分钟走了10千米，故乙车速度为60千米/时，甲车速度为30千米/时。故选择D项。
以上就是关于行程问题中相遇追及模型基本公式的应用。在解题中分析好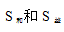
，套用公式即可，在这里提醒大家，不管是相遇还是追及问题，公式中的t都是同时运动的时间。
等距离求平均速度
一、概述
数量关系一直以来因考查范围广、难度大、用时多而让很多考生头疼，但是在实际考试中，又是不能放弃的一个重要板块，所以必须要有攻克数量关系的决心。今天带大家学习行程问题之等距离求平均速度。
二、适用环境及公式推导
三、题型认知
例题：在村村通公路的社会主义新农村建设中，有两个山村之间的公路都是上坡和下坡，没有平坦路。农车上坡的速度保持20千米/小时，下坡的速度保持30千米/小时，已知农车在两个山村之间往返一次，需要行驶4小时，问两个山村之间的距离是多少千米（ ）？
A.45 B.48 C.50 D.24
【答案】B【解析】方法一，解析：如下图，设两个山村之间的公路是先上坡再下坡，上坡的路程为S₁千米，下坡的路程为S₂千米，则返回时上坡的路程为S₂米，下坡的路程为S₁米。根据往返共用4小时可得，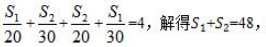
即两个山村之间的距离是48千米。
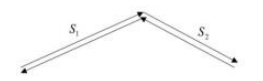
总结1：考试中，可以直接根据题干的描述列出相应的等量关系来进行求解，但是使用这种方法解析所用时间会更多。下面介绍一下等距离求平均速度的方法如何来求解整个题目。
方法二，解析：根据题意，两个山村之间进行往返，上坡和下坡距离相等，都是两山村之间的距离。可利用等距离平均速度，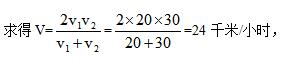
即往返的平均速度就是24千米/小时，往返总时间是4小时，故往返总路程为24×4=96千米，则两个山村的距离为96÷2=48千米。
总结2：分析整个题干会发现，在往返过程中，总上坡路程与总下坡路程相等，出现“上下坡”、“往返”等字眼，可以先求出平均速度，再结合往返总时间，求出往返总路程，最后根据问题描述求解题目。
通过上述题目和总结，大家可以感受到要想掌握行程问题之等距离求平均速度，一方面要掌握题型的特征，了解这一类题目的特征能让我们明确如何下手；另一方面是学习该知识点的相关技巧，更要对不同知识点多做总结，才能帮助我们提高学习效果。
利用正反比巧解行程问题
行程问题是行测数量关系中的常考题型，但是很多考生对于此类问题做题时间较长，甚至束手无策，因此有些考生会选择放弃。若能熟练地运用行程问题中存在的正反比关系，就能比较快速地解决一部分的行程问题。
一、正反比关系
基本公式：路程=速度×时间
当路程一定时，速度越快，时间越短，即路程一定，速度与时间成反比；
当时间一定时，速度越快，路程越远，即时间一定，路程与速度成正比；
当速度一定时，时间越长，路程越远，即速度一定，路程与时间成正比。
注意：应用正反比一定要找到不变的量，在不变量下才可以应用正反比。
二、在行程问题中的应用
例1：空军某部队运送救灾物资到灾区。原计划飞机每分钟飞行12千米，由于灾情严重，飞机速度提高到每分钟15千米，结果比原计划提前30分钟到达目的地。则机场到灾区的距离是（ ）千米。
A.1600 B.1800 C.2050 D.2250
【答案】B【解析】不难发现，无论速度如何发生变化，飞机飞行的路程都是从机场到灾区，即路程一定，此时速度和时间成反比。根据题意可知原计划与实际飞行的速度之比为12：15，即4：5，那么所花时间之比为5：4，原计划所用时间比实际多1份，对应30分钟，那么实际使用时间为4×30=120分钟，则机场到灾区的距离是15×120=1800km，故选B。
例2：甲、乙两辆车从A地驶往90公里外的B地，两车的速度比为5：6，甲车于上午10点半出发，乙车于10点40分出发，最终乙车比甲车早2分钟到达B地，问乙车是在何时追上甲车的（ ）？
A.11：16 B.11：25 C.11：30 D.11：34
【答案】C【解析】根据题干条件作图如下，甲、乙两车均从A地出发，假设在C地乙车追上了甲车，那么此时甲、乙两车行驶的路程相同(均为AC)，已知两车的速度比为5：6，则时间之比为6：5，甲比乙多用了1份时间，对应甲比乙早出发的10分钟，则甲从A地到C地用时6×10=60分钟=1小时，所以甲在11点半被乙追上，故选C。
