
行测数量关系考点——浓度问题
知识引导
浓度问题是行测数量关系中的常见知识点,但是很多考生遇到浓度问题时会“认为”复杂而不愿意做从而放弃。那么今天就谈谈浓度问题的常见题型及解法,希望对大家有所助益。
相关概念
浓度问题涉及到的概念主要有三个:即溶质、溶剂、溶液。比如将盐溶解到水中,那么盐即为溶质,水即为溶剂,盐与水的混合物即为溶液。
核心公式
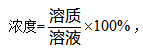 其中溶液=溶质+溶剂,一般整体考虑即可,不需要拆开计算。
其中溶液=溶质+溶剂,一般整体考虑即可,不需要拆开计算。
解题方法
公式法、方程法、特值法。
具体可以通过下面三道例题来学习。
练习题
例1:将浓度为15%和5%的盐水各1000克,分别倒出若干配置成浓度为10%的盐水1200克,将剩下的盐水全部混合在一起,得到的盐水浓度为( )。
A.8% B.10% C.12% D.14%
【答案】B【解析】题干中将浓度15%和5%的盐水的溶液倒出,配置成新浓度的盐水,发现没有加入新的溶质,则配置前的溶质和=配置后10%浓度盐水的溶质+剩下盐水的溶质。两个盐水总的溶质为15%×1000+5%×1000=200g。已经倒出的溶质为10%×1200=120g。剩下的溶质为200-120=80g,剩下的溶液为1000+1000-1200=800g。则剩下的盐水浓度为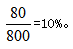 因此,选择B选项。
因此,选择B选项。
例2:甲乙两种盐水,浓度分别为10%和40%,且乙盐水的量比甲盐水多1.5x克,现将两种溶液混合,并加入2x克水,最终得到浓度为20%的盐水。问乙盐水的含盐量是甲盐水的多少倍?( )
A.3倍 B.6倍 C.7.5倍 D.10倍
【答案】D【解析】设甲盐水的量为y克,则乙盐水的量为y+1.5x克。根据题意可得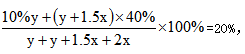 解得y=x。甲盐水中含盐量为10%y=0.1x,乙盐水中含盐量为40%×(x+1.5x)=x,因此所求为x÷0.1x=10倍。因此,选择D选项。
解得y=x。甲盐水中含盐量为10%y=0.1x,乙盐水中含盐量为40%×(x+1.5x)=x,因此所求为x÷0.1x=10倍。因此,选择D选项。
例3:某种溶液的浓度为20%,加入水后溶液的浓度变为15%。如果再加入同样多的水,则溶液浓度变为( )。
A.9% B.10% C.11% D.12%
【答案】D【解析】题干中没有加入新的溶质,则加入水前后溶质不变。此时给溶液赋值100g,则溶质为20%×100=20g。加入水后溶质不变依然为20g,但浓度变为15%,因20400400100此溶液为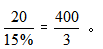 。第一次加水
。第一次加水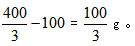 再加一次水后溶液为
再加一次水后溶液为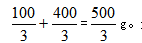 最终溶液浓度为
最终溶液浓度为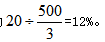 因此,选择D选项。
因此,选择D选项。
浅谈浓度问题的解决思路
浓度问题在行测考试中还是总能见到的,通常题干不长,条件不多,所以是值得一做的题目类型,但是麻烦之处在于通常浓度问题的考察会涉及多种溶液进行混合,所以如果不能准确把握题目的核心,做起来仍是有些耗时,那么接下来就谈谈如何既快又准确地解决此类问题。
浓度问题通常涉及的都是溶液混合,解决此类问题,首先要明白的就是溶质的重要性,因为在多个溶液进行混合时,我们需要用一个量,把这些参与混合的溶液串联起来,而由于基本考察的都是同种溶液混合,溶质之间可以直接加减,溶液和浓度再随之而改变,以这样的一个思想去把握题目,其实是比较清楚的,接下来我们看两道题。
【例题1】使用浓度为60%的硫酸溶液50克和浓度为90%的硫酸溶液若干克,配制浓度为66%的硫酸溶液100克,需要加水的质量是( )?
A.10克 B.12克 C.15克 D.18克
【答案】A【解析】这道题我们可以简单理解为两种溶液混合成一个新溶液,所求的是混合时加的水,按照刚才的思想,我们首先想到的应该是弄清楚溶质的量,再根据溶质得出各部分溶液的质量,最后求得加水量。所以可以简单口算得到其中一种溶液的溶质是30克,另一个虽然不清楚,但是混合后的溶液溶质是66克,所以可以得出另一种溶液溶质是36克,结合其浓度,就可以知道需要该种溶液质量为40克,那么两种溶液综合溶液就是90克,而混合后溶液是100克,所以加了10克水。所以答案是A。
【例题2】某化学实验室有A、B、C三个试管分别盛有10克、20克、30克水,将某种盐溶液10克倒入试管A中,充分混合均匀后,取出10克溶液倒入B试管,充分混合均匀后,取出10克溶液倒入C试管,充分混合均匀后,这时C试管中溶液浓度为1%,则倒入A试管中的盐溶液浓度是( )?
A.40% B.36% C.30% D.24%
【答案】D【解析】这道题同样也是浓度问题,通过多次混合,最后求最初的溶液浓度,那么按照刚才所讲的思想,我们一样先研究清楚溶质的变化情况,再根据最后一次混合后的浓度和溶液质量得出具体溶质的值,最后得出初始溶液浓度。那么首先第一次混合,溶质没有变化,但是溶液变成两倍也就是20克,那么取出10克,取出了溶液的一半,那么取出的溶质也应该是一半,第二次混合溶质还是没变,但是溶液变成了原来的三倍。而取出了还是10克,取出的溶液是三分之一,所以也取出了三分之一的溶质,所以第三次混合时候的溶质是初始溶质的六分之一,而由于此时溶液是40克,结合浓度,此时溶质应该是0.4克,所以初始溶质应该是0.24克,而初始溶液是10克,所以初始浓度是24%。所以答案是D。
通过分析这两个题目,我们可以发现抓住溶质再研究溶液和浓度等量,对于解题来说是有一定帮助的,但是想要精通此类问题,还是需要考生在后续的学习中,多练习多总结,这样更有助于对于题目的核心和方向有一定的把握。最后希望大家能取得一个好的成绩。
巧解浓度问题
浓度问题是行测的常考题型之一。此类题目考察灵活,且与生活息息相关,故深受命题人青睐。那么,如何在考试中,对此类问题进行有针对性的处理,就成为接下来在本文要研究的重点。
第一、利用基础知识解题
我们在解决浓度问题时,时常会遇到一些相对简单的题目,利用好浓度问题的基础知识就能轻松解题,下面我们就通过例题来了解一下:
例:王老师将天然蜂蜜和矿泉水混合成蜂蜜水,现有一瓶浓度为10%的蜂蜜100克,如果需要将蜂蜜水的浓度提高10个百分点,需加入天然蜂蜜a克和矿泉水2a克,那么后加入的蜂蜜是原来的:( )
A.1倍 B.1.5倍 C.2倍 D.2.5倍
【答案】D【解析】100克浓度为10%的蜂蜜水含蜂蜜100×10%=10克。加入a克蜂蜜和2a克矿泉水后浓度变为10%+10%=20%,则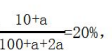 解得a=25。后加入的蜂蜜是原来的25÷10=2.5倍。
解得a=25。后加入的蜂蜜是原来的25÷10=2.5倍。
基础知识:溶液=溶质+溶剂,
在本题中,溶质为蜂蜜,溶剂为矿泉水,而溶液为蜂蜜的水溶液,即蜂蜜+矿泉水。
第二、利用方程法解题
基本含义
浓度问题研究的是溶质、溶剂和溶液三者之间的关系。例:500克浓度为40%的盐水,其中溶质为盐,溶剂为水,盐的质量和水的质量之和为盐水的溶液质量,其质量为500克。如果水的量不变,那么盐加得越多,盐水就越咸,盐水咸的程度是由盐(溶质)与盐水(溶液=盐+水)二者量的比值决定的。浓度就是溶质的量与溶液的量的比值,通常用百分数表示。
基本公式
在做题过程中,通常忽略掉溶液之间的化学反应,将混合后的溶液质量(或体积)等于混合前的溶液质量(或体积)相加;混合后的溶质质量(或体积)等于混合前的溶质质量(或体积)相加。

例1:某饮料店有纯果汁(即浓度为100%)10千克,浓度为30%的浓缩还原果汁20千克。若取纯果汁、浓缩还原果汁各10千克倒入10千克纯净水中,再倒入10千克的浓缩还原果汁,则得到的果汁浓度为( )。
A.40%
B.37.5%
C.35%
D.30%
【答案】A【解析】由题干描述可知,混合后果汁总量,即溶液为40千克,其中纯果汁含量为10+30%×20=16千克,则得到果汁的浓度为: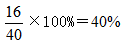 ,故答案选A。
,故答案选A。
例2:有两瓶质量均为100克且浓度相同的盐溶液,在一瓶中加入20克水,在另一瓶中加入50克浓度为30%的盐溶液后,它们的浓度仍然相等,则这两瓶盐溶液原来的浓度是( )。
A.36%
B.64%
C.50%
D.60%
【答案】D【解析】由题干描述可知,两瓶溶液经过不同的方式混合后,其浓度仍然相等,可据此建立等量关系。设两瓶盐溶液原来浓度为x%,则它们的含盐量为x,根据题意有: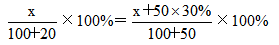 ,解得x=60,即原来浓度为60%,故答案选D。
,解得x=60,即原来浓度为60%,故答案选D。
第三、十字交叉巧解题
由上面例题我们发现,浓度问题经常涉及溶液混合的问题。而当溶液A和溶液B混合后,其混合后的溶液浓度应为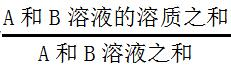 ,故符合分子分母具有可加性的比值混合规律,因此,我们可以采用十字交叉来解决溶液混合问题。例题如下:
,故符合分子分母具有可加性的比值混合规律,因此,我们可以采用十字交叉来解决溶液混合问题。例题如下:
例:现有浓度为10%的盐水20千克,为得到浓度为22%的盐水,应再加入浓度为30%的盐水( )千克。
A.30 B.33 C.36 D.39
【答案】A【解析】根据十字交叉法:
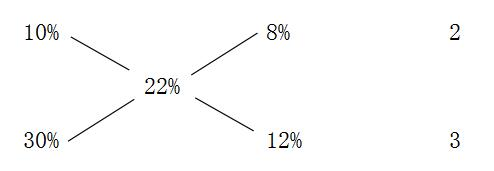
得到浓度为10%的盐水与浓度为30%的盐水的质量比为8%∶12%=2∶3,故本题所求为30千克,选择A。
在行测考试中,因为题量大和时间的限制,很多时候需要在做题方法上尽可能做到快速、高效。而以上几种针对浓度问题的解决思路及方法大家可以在以后的训练中小试身手,希望在真正的考场上各位在解决浓度问题上能游刃有余。








