政华公考

【答案】B【解析】设工作总量为20（20、10的最小公倍数），从而易知，甲、乙的效率分别为1、2。这里的循环周期为2天（甲、乙各1天），一个循环周期的效率和为3，20÷3=6……2，这里的6即为6个循环周期，对应12天，剩余的2个工作量，甲、乙各做1个工作量，甲做1个工作量对应1天，乙做1个工作量对应0.5天。所以，共需12+1+0.5=13.5天。答案选B。

例2：一条隧道，甲单独挖要20天完成，乙单独挖要10天完成。如果乙先挖1天，然后甲接替乙挖1天，再由乙接替甲挖1天，两人如此交替工作。那么，挖完这条隧道共用多少天（）？

A.13 B.13.5 C.14 D.15.5

【答案】A【解析】设工作总量为20（20、10的最小公倍数），从而易知，乙、甲的效率分别为2、1。这里的循环周期为2天（乙、甲各1天），一个循环周期的效率和为3，20÷3=6……2，这里的6即为6个循环周期，对应12天，剩余的2个工作量，乙做一天正好完成。所以，共需12+1=13天。答案选A。

当然，也有一部分题目通过有参与合作的主体正效率也有负效率来提升难度。

例3：一个水池有一条进水管和一条出水管，单开进水管4个小时注满，单开出水管6个小时放空，如果按照先单独开进水管一个小时，再单独开出水管一个小时的顺序循环轮流开放两个水管，那么经过多少个小时后，水池里面的水开始溢出。（）

A.8个小时 B.19个小时 C.20个小时40分钟 D.24个小时

【答案】C【解析】结合特值思想，可以假设水池容量为12L，则进水管一个小时进水3L，出水管一个小时出水2L，按照题意，每两个小时实际进水1L。9个周期之后，18个小时，水池里面有9L水，此时开进水管1个小时，进3L水，刚好注满却没溢出，再开一个小时出水管，

出水2L，再开40分钟，水池里面的水开始溢出，所以所求时间为20个小时40分钟。

通过以上题目，相信考生能够清楚交替合作的解题关键在于找到循环，再利用循环解决问题。希望考生利用备考时间查缺补漏，争取笔试高分，为面试守擂打下坚实基础！

特值法在工程问题中的妙用

工程问题是行测考试中的热门题型，其中又以多者合作这类题型尤为常考，多者合作指一项工程是由两个或两个以上对象合作完成，解决该类问题的关键点在于梳理清楚合作时每个阶段的工作情况，通常我们会结合工程问题的基本公式去构建方程。此外，我们也经常使用特值法解多者合问题，下面跟大家分享几种在工程问题中常用的设特值的方法：

一、将甲、乙完成天数的最小公倍数设为工作总量

【例1】项目部接到一项工程，若该工程由甲组单独完成需要30天，若由乙组单独完成则需要20天。现在由于时间关系，两个项目组共同合作，需要多少天才能完成这项工程（）？

A.8 B.12 C.14 D.18

【答案】B【解析】设工作总量为60，可得甲工作效率为2，乙的工作效率为3，因此他们的合作效率为5，合作完成所需时间为60÷5=12天，故选择B。

二、将效率比直接设为效率

【例2】某市有甲、乙、丙三个工程队，工作效率比为3：4：5。一项工程先由甲工作4天，再由甲、乙合作5天，最后由乙单独工作7天即可完成。问这项工程由丙单独完成需要多少天？

A.12 B.15 C.18 D.21

【答案】B【解析】根据效率比设甲的效率为3，乙的效率为4，丙的效率为5，则这项工程的工作总量为4×3+5×（3+4）+7×4=75，因此丙单独完成需要75÷5=15天，故选B。

三、多个对象合作，且每个对象的工作效率一样时，设每个对象的工作效率为1

【例3】公司安排100名工人去修一条公路，假设每个工人每月的工作效率一样，计划10个月完成该项工程，工作2个月后，由于特殊情况，需提前3个月完工，为保证按时完工，则需增加多少名工人？

A.40 B.50 C.60 D.70

【答案】C【解析】设每个工人每月的工作效率为1，为保证提前3个月完工，需增加x名工人，根据工程总量保持不变可得1×100×10=1×100×2+1×（100+x）×（10-2-3），解得x=60，因此选择C。

行测数量关系简便方法之特值法

多者合作问题是行测数量关系工程问题中常见的一种，研究的也是工作总量、效率、时间之间的关系。但是它和普通工程问题不同的是，这种问题是多个主体去完成同一项工程，那么工作效率就会变成多者的效率和。这是做多者合作题目的关键。了解了这个之后，大家还要明白的一点就是我们如何能够用更简洁的方法去做出来，才能更好地去平衡考场中正确率和时间的问题。其实适合多者合作问题的简便方法就是特值法。这个方法可以很快地帮助大家去抽丝剥茧，从而解出答案。下面就简单说一下特值法在此类题型中的应用。

类型一：已知多个完工时间，将工作总量设为时间的最小公倍数

例题：有一项工作，甲单干需要10个小时完成，乙单干需要12个小时完成。甲、乙两人同时工作5小时后，甲另有其他的事情去做，只有乙继续工作，那么完成这项工作共用了（）小时。

A.5 B.6 C.7 D.8

【答案】B【解析】假设总工作量为60（10和12的最小公倍数），则甲的工作效率是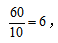乙的工作效率是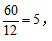则甲、乙合作5小时后还剩工作量为60-（6+5）×5=5，乙还需工作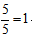小时，所以完成这项工作共用5+1=6小时，故选B。

类型二：给出最简效率比，直接将最简效率比设为特值

例题：某医疗器械公司为完成一批口罩订单生产任务，先期投产了A和B两条生产线，A和B的工作效率之比是2∶3，计划8天可完成订单生产任务。两天后公司又投产了生产线C，A和C的工作效率之比为2∶1。问：该批口罩订单任务将提前几天完成？（）

A.1 B.2 C.3 D.4

【答案】A【解析】由题意可知，A、B、C的工作效率之比为2∶3∶1。因此可设A的工作效率为2，B的工作效率为3，C的工作效率为1，则生产任务总量为（2+3）x8=40。根据“两天后公司又投产了生产线C”可知，先由A和B合作生产两天，完成生产任务总量为（2+3）x2=10，则剩余任务量由A、B、C共同完成，其合作时间为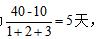故完成全部任务共用时2+5=7天，则该批口罩订单任务将提前8-7=1天完成，选A。

类型三：团队合作，将每个元素的工作效率设为“1”

例题：修一条公路，假设每人每天的工作效率相同，计划180名工人1年完成，工作4个月后，因特殊情况，要求提前2个月完成任务，则需要增加工人多少名？（）

A.50 B.65 C.70 D.60

【答案】D【解析】设每名工人每月的工作量为1，则全部工作量为180×12=2160，工作4个月完成工作量180×4=720。要想提前2个月完成，假设需要增加工人x名，则有180×4+（180+x）×（12-4-2）=180×12，解得x=60，选D。

小结

对于行测数量关系中的多者合作，不同题干信息用不同的特值方法，具体有如下三种：

1.已知多个完工的时间，设工程总量为多个完工时间的最小公倍数，进而求出各自工作效率。

2.已知多个对象之间工作效率的比例关系，直接将最简效率比设为特值，进而反推出工程总量进一步根据题干要求求解。

3.已知若干相同元素做同一项工程且每个元素工作效率相同，设每个元素工作效率为单位1，进而可求出工程总量再进一步根据题干要求求解即可。